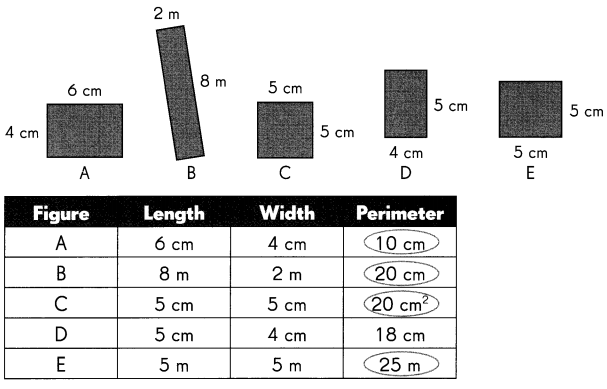
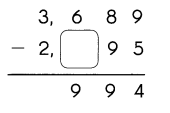
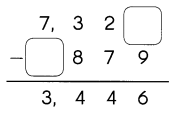
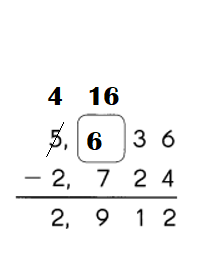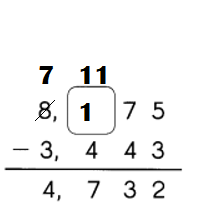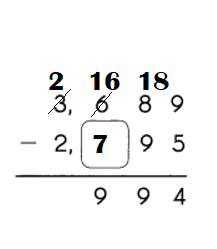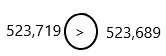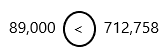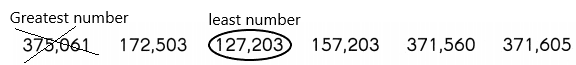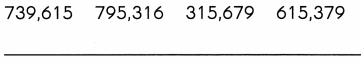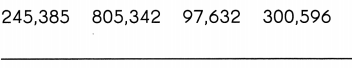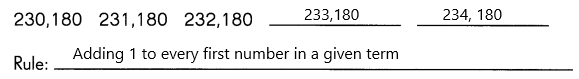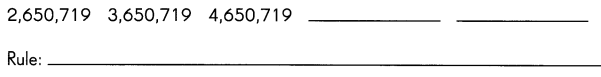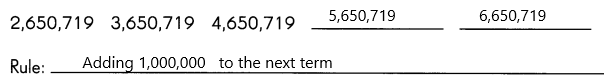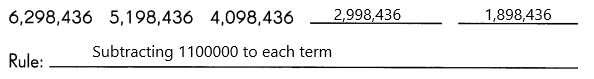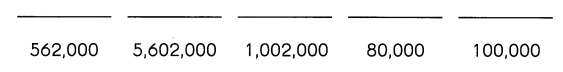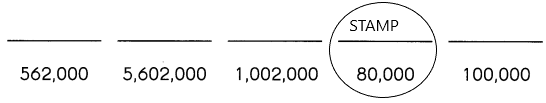Go through the Math in Focus Grade 5 Workbook Answer Key Chapter 1 Practice 4 Comparing Numbers to 10,000,000 to finish your assignments.
Math in Focus Grade 5 Chapter 1 Practice 4 Answer Key Comparing Numbers to 10,000,000
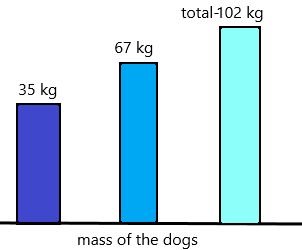
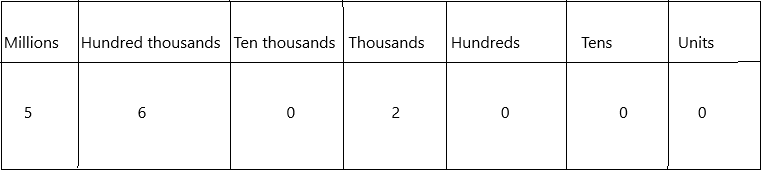
Complete the place-value chart. Then use it to compare the numbers.
Question 1.
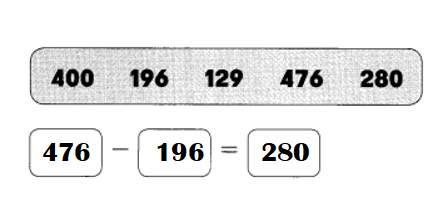
Which is greater, 197,210 or 225,302?
Compare the values of the digits, working from left to right.

___ hundred thousands is greater than ___ is greater than
So, ___ is greater than ____
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.

A whole number is larger than another if it has more digits. If the number of digits in each number is the same, then look at the digits from left to right. If the left digit is larger in one number, then this is the largest number. If this digit is the same, compare the next digit along to the right.
Now compare the numbers: 197,210 and 222,302
1 is less than 2 so 197,210 is less than 222,302. Because In hundred thousand place 1 is smaller than 2.
197,210<222,302
Fill each  with >or <.
with >or <.
Question 2.
128,758  74,906
74,906
Answer:>
A whole number is larger than another if it has more digits. If the number of digits in each number is the same, then look at the digits from left to right. If the left digit is larger in one number, then this is the largest number. If this digit is the same, compare the next digit along to the right.

1. We are comparing the numbers 128,758 and 74,906.
2. The order of digits from smallest to largest is 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
3. We start with the place value column on the left.
4. 1 is greater than o because in the first number the hundred thousand place is 1 and in the second number there is no hundred thousand place so it becomes zero.
5. Therefore, 128,758 is greater than 74,906.
6. The comparison symbol for greater than is >, pointing to the smaller number of 74,906.
Question 3.
523,719  523,689
523,689
Answer: >
A whole number is larger than another if it has more digits. If the number of digits in each number is the same, then look at the digits from left to right. If the left digit is larger in one number, then this is the largest number. If this digit is the same, compare the next digit along to the right.
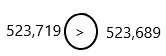
1. We are comparing the numbers 523,719 and 523,689.
2. The order of digits from smallest to largest is 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
3. We start with the place value column on the left.
4. Both numbers are having the same digit in the hundred thousand, ten thousand, thousands column.
5. Now we compare the next digit. It means now we have to compare hundreds place and the digits are 7 and 6.
6. 7 is greater than 6 in order of digits.
7. Therefore, 523,719 is greater than 523,689.
8. The comparison symbol for greater than is >, pointing to the smaller number of 523,689.
Question 4.
89,000  712,758
712,758
Answer:
A whole number is larger than another if it has more digits. If the number of digits in each number is the same, then look at the digits from left to right. If the left digit is larger in one number, then this is the largest number. If this digit is the same, compare the next digit along to the right.
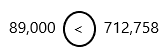
1. We are comparing the numbers 89,000 and 712,758.
2. The order of digits from smallest to largest is 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
3. We start with the place value column on the left.
4. 0 is less than 7 because the first number in the hundred thousand place is 0 because there is no digit in that place and in the second number the digit of hundred thousand place is 7.
5. Therefore, 89,000 is less than 712,758.
6. The comparison symbol for less than is <, pointing to the greater number of 712,758.
Question 5.
635,002  635,100
635,100
Answer:
A whole number is larger than another if it has more digits. If the number of digits in each number is the same, then look at the digits from left to right. If the left digit is larger in one number, then this is the largest number. If this digit is the same, compare the next digit along to the right.
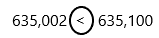
1. We are comparing the numbers 635,002 and 635,100.
2. The order of digits from smallest to largest is 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
3. We start with the place value column on the left.
4. Both numbers are having the same digit in the hundred thousand, ten thousand, thousands column.
5. Now we compare the next digit. It means now we have to compare hundreds place and the digits are 0 and 1.
6. 0 is less than 1 in order of digits.
7. Therefore, 635,002 is less than 635,100.
8. The comparison symbol for less than is <, pointing to the bigger number of 635,100.
Circle the least number and cross out the greatest number.
Question 6.
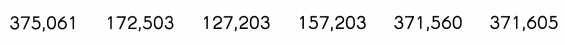
Answer:
The least to greatest is a concept in a number system where the given set of numbers is arranged in an ascending order or least value to the greatest value.
In the given numbers we need to find out the least number and greatest number and then we need to circle for the least number and cross mark for the greatest number.
1. Apply the comparison method to get the least number and greatest number.
2. Compare each digit present in the place values.
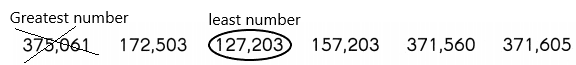
Order the numbers from least to greatest.
Question 7.
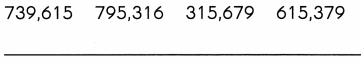
Answer: 315,679, 615,379, 739,615, 795,316.
Note: Least to greatest means ascending order.
Ascending order definition: Ascending order is a method of arranging numbers from smallest value to largest value. The order goes from left to right. Ascending order is also sometimes named as increasing order.
For example, a set of natural numbers are in ascending order, such as 1 < 2 < 3 < 4 < 5 < 6 < 7 < 8… and so on. The less than symbol (<), is used to denote the increasing order.
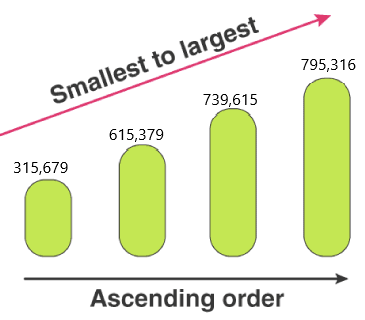
The word ‘ascending’ means going up. Hence, in the case of Mathematics, if the numbers are going up, then they are arranged in ascending order.
The other terms used for ascending order are:
1. Lowest value to highest value
2. Bottom value to Top value
These numbers can be written by using the ascending symbol: 315,679< 615,379< 739,615< 795,316.
The symbol represents that the succeeding number is greater than the preceding number in the arrangement.
Question 8.
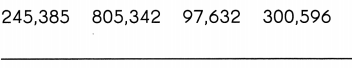
Answer: 97,632, 245,385, 300,596, 805,342.
Ascending order definition: Ascending order is a method of arranging numbers from smallest value to largest value. The order goes from left to right. Ascending order is also sometimes named as increasing order.
For example, a set of natural numbers are in ascending order, such as 1 < 2 < 3 < 4 < 5 < 6 < 7 < 8… and so on. The less than symbol (<), is used to denote the increasing order.
The word ‘ascending’ means going up. Hence, in the case of Mathematics, if the numbers are going up, then they are arranged in ascending order.
The other terms used for ascending order are:
1. Lowest value to highest value
2. Bottom value to Top value
These numbers can be written by using the ascending symbol: 97,632< 245,385< 300,596< 805,342.
The symbol represents that the succeeding number is greater than the preceding number in the arrangement.
Compare the numbers. Use the place-value chart to help you.
Question 9.
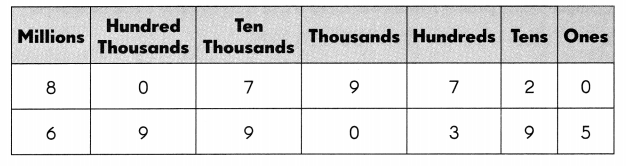
_______ millions is less than ____________________ millions.
_______ is less than ___________________ .
Answer: 6 million is less than 8 million
6,990,395 is less than 8,079,720.
A whole number is larger than another if it has more digits. If the number of digits in each number is the same, then look at the digits from left to right. If the left digit is larger in one number, then this is the largest number. If this digit is the same, compare the next digit along to the right.
1. We are comparing the numbers 8,079,720 and 6,990,395
2. The order of digits from smallest to largest is 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
3. We start with the place value column on the left.
4. 6 is less than 8 because the digits of the millions place 6 and 8
5. Therefore, 6,990,395 is less than 8,079,720.
6. The comparison symbol for less than is <, pointing to the greater number of 8,079,720.
Question 10.
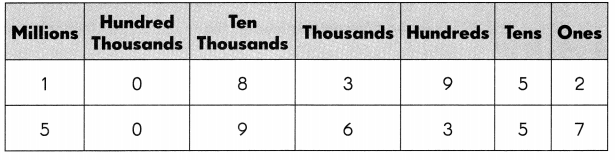
___ is greater than ____
Answer:5,096,357 is greater than 1,083,952.
A whole number is larger than another if it has more digits. If the number of digits in each number is the same, then look at the digits from left to right. If the left digit is larger in one number, then this is the largest number. If this digit is the same, compare the next digit along to the right.
1. We are comparing the numbers 5,096,357 and 1,083,952
2. The order of digits from smallest to largest is 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
3. We start with the place value column on the left.
4. 5 is greater than 1 because the digits of the millions place 5 and 1
5. Therefore, 5,096,357 is less than 1,083,952.
6. The comparison symbol for greater than is >, pointing to the less number of 1,083,952.
Question 11.
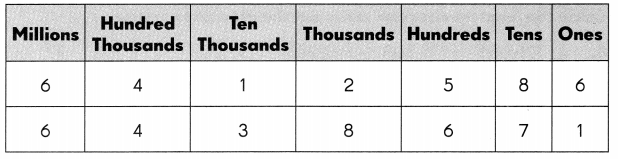
___ is greater than ____
Answer:6,438,671 is greater than 6,412,586.
A whole number is larger than another if it has more digits. If the number of digits in each number is the same, then look at the digits from left to right. If the left digit is larger in one number, then this is the largest number. If this digit is the same, compare the next digit along to the right.
1. We are comparing the numbers 6,438,671 and 6,412,586
2. The order of digits from smallest to largest is 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
3. We start with the place value column on the left. The digits of millions and hundred thousands place are the same.
4. Now compare the next digits.
5. 3 is greater than 1 because the digits of the ten thousands place 3 and 1
6. Therefore, 6,438,671 is less than 6,412,586.
7. The comparison symbol for greater than is >, pointing to the less number of 6,412,586.
Fill each  with > or <.
with > or <.
Question 12.
4,015,280  2,845,000
2,845,000
Answer: >
The greater than symbol in maths is placed between two values in which the first number is greater than the second number. In inequality, greater than symbol is always pointed to the greater value and the symbol consists of two equal length strokes connecting at an acute angle at the right. ( >).
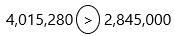
1. We are comparing the numbers 4,015,280 and 2,845,000
2. The order of digits from smallest to largest is 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
3. We start with the place value column on the left.
5. 4 is greater than 2 because the digits of the millions place 4 and 2
6. Therefore, 4,015,280 is greater than 2,845,000.
7. The comparison symbol for greater than is >, pointing to the less number of 2,845,000.
Question 13.
999,098  1,000,000
1,000,000
Answer:
A less than symbol is placed between two numbers where the first number is less than the second number. In inequality, less than symbol points to the smaller value where the two equal length strokes connect at an acute angle at the left (<).
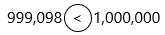
1. We are comparing the numbers 999,098 and 1,000,000
2. The order of digits from smallest to largest is 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
3. We start with the place value column on the left.
5. 0 is less than 1 because the digits of the millions place 0 and 1
6. Therefore, 999,098 is less than 1,000,000.
7. The comparison symbol for less than is <, pointing to the greater number of 1,000,000.
Question 14.
2,007,625  2,107,625
2,107,625
Answer:
A less than symbol is placed between two numbers where the first number is less than the second number. In inequality, less than symbol points to the smaller value where the two equal length strokes connect at an acute angle at the left (<).

1. We are comparing the numbers 2,007,625 and 2,107,625.
2. The order of digits from smallest to largest is 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
3. We start with the place value column on the left.
5. 0 is less than 1 because the digits of the hundred thousand place 0 and 1
6. Therefore, 2,007,625 is less than 2,107,625.
7. The comparison symbol for less than is <, pointing to the greater number of 2,107,625.
Question 15.
7,405,319  905,407
905,407
Answer:
The greater than symbol in maths is placed between two values in which the first number is greater than the second number. In inequality, greater than symbol is always pointed to the greater value and the symbol consists of two equal length strokes connecting at an acute angle at the right. ( >).
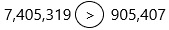
1. We are comparing the numbers 7,405,319 and 905,407
2. The order of digits from smallest to largest is 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
3. We start with the place value column on the left.
5. 7 is greater than 0 because the digits of the millions place 7 and 0. In the second number, there is no millions place. So it becomes zero.
6. Therefore, 7,405,319 is greater than 905,407.
7. The comparison symbol for greater than is >, pointing to the less number of 905,407.
Order the numbers from greatest to least.
Question 16.

Answer: 3,190,000 2,720,000 2,432,000 480,000
Note: Greatest to least means descending order.
Descending order definition: In simple words, descending order is defined as an arrangement in the highest to lowest format. These concepts are related to decimals, numbers, fractions or amounts of money. This is also known as decreasing the order of numbers.
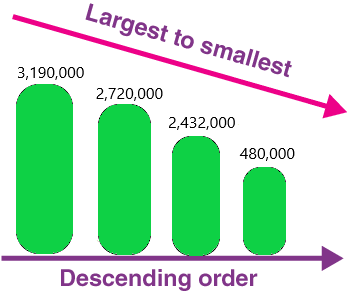
The symbol used to represent the order in descending form is ‘ > ‘. The given numbers can be represented in this form using the descending symbol as 3,190,000>2,720,000>2,432,000>480,000.
Question 17.

Answer:3,150,000 2,020,000 913,000 513,900
Descending order definition: In simple words, descending order is defined as an arrangement in the highest to lowest format. These concepts are related to decimals, numbers, fractions or amounts of money. This is also known as decreasing the order of numbers.
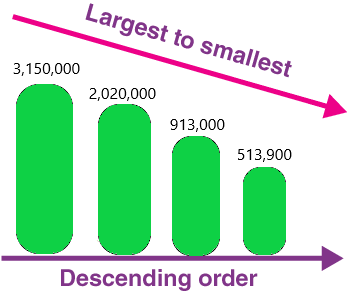
The symbol used to represent the order in descending form is ‘ > ‘. The given numbers can be represented in this form using the descending symbol as 3,150,000>2,020,000>913,000>513,900.
Find the missing numbers.
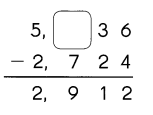
Question 18.
738,561 938,561 1,138,561 …
a. 938,561 is ___ more than 738,561.
Answer: 200,000
Explanation:
To get the answer we need to subtract 938,561 and 738,561.

Therefore, 200,000 is more than 738,561.
b. 1,138,561 is ___ more than 938,561.
Answer: 200000
Explanation:
To get the answer we need to subtract 1,138,561 and 938,561.

Therefore, 200,000 is more than 938,561.
c. ____ more than 1,138,561 is ____
Answer: 200,000
We are looking for a new number which is 200000 more than 1138561.
We will get the new number by adding 200000 to 1138561.
We write it down as:
1138561+200000=1338561
d. The next number in the pattern is ____
Answer:1,338,561
In Mathematics, number patterns are the patterns in which a list number follows a certain sequence. Generally, the patterns establish the relationship between two numbers. It is also known as the sequence of series in numbers.
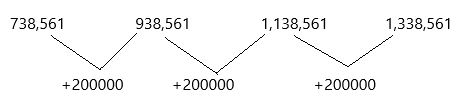
Observation of number patterns can guide to simple processes and make the calculations easier.
By adding 200000 to the number we get the next number.
738,561+200000=938,561
938,561+200000=1,138,561
1,138,561+200000=1,338,561.
Therefore, the next number in the pattern is 1,338,561.
Question 19.
4,655,230 4,555,230 4,455,230 …
a. 4,555,230 is ___ less than 4,655,230.
Answer: 100000
Explanation:
To get the answer to add 100000 to the 4,555,230

Therefore, 100000 less to the 4,555,230 from the 4,6555,230.
b. 4,455,230 is ___ less than 4,555,230.
Answer: 100000
To get the answer to add 100000 to the 4,455,230

Therefore, 100000 less to the 4,455,230 from the 4,555,230.
c. ___ less than 4,455,230 is ____
Answer: We are looking for a new number which is 4455230 less than 100000.
We will get the new number by subtracting 4455230 from 100000.
We write it down as:
4455230-100000=4355230
d. The next number in the pattern is ____
Answer:
In Mathematics, number patterns are the patterns in which a list number follows a certain sequence. Generally, the patterns establish the relationship between two numbers. It is also known as the sequence of series in numbers.
Observation of number patterns can guide to simple processes and make the calculations easier.

By subtracting 100000 to the number we get the next number.
4,655,230-100000=4,555,230
4,555,230-100000=4,455,230
4,455,230-100000=4,355,230.
Therefore, the next number in the pattern is 4,355,230.
Find the rule. Then complete the number patterns.
Question 20.

Answer: 233,180 234,180
It is an arithmetic pattern.
Definition: The arithmetic pattern is also known as the algebraic pattern. In an arithmetic pattern, the sequences are based on the addition or subtraction of the terms. If two or more terms in the sequence are given, we can use addition or subtraction to find the arithmetic pattern.
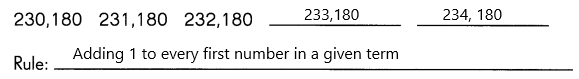
The given terms are 230,180 231,180 232, 180 – – Now find the missing term in the sequence.
Here, we can use the addition process to figure out the missing terms in the patterns.
In the pattern, the rule used is “Add 1 to the previous term to get the next term”.
Now take the second term 231, 180 If we add 1 to the second term (231), we get the third term (232) and the 180 repeats like that.
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 232. Therefore, 232+1 = 233.
Second missing term: The previous term is 233. So, 233+1 = 234.
Hence, the complete arithmetic pattern is 230, 180 231, 180 232, 180 233, 180 234,180.
Question 21.

Answer: 835, 400 830, 400
It is an arithmetic pattern.
Definition: The arithmetic pattern is also known as the algebraic pattern. In an arithmetic pattern, the sequences are based on the addition or subtraction of the terms. If two or more terms in the sequence are given, we can use addition or subtraction to find the arithmetic pattern.

The given terms are 850, 400 845, 400 840, 400 – – Now find the missing term in the sequence.
Here, we can use the subtraction process to figure out the missing terms in the patterns.
In the pattern, the rule used is “subtract 5 to the previous term to get the next term”.
Now take the second term 845, 400 If we subtract 5 to the second term (845), we get the third term (840) and the 400 repeats like that.
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 840. Therefore, 840-5 = 835.
Second missing term: The previous term is 835. So, 835-5 = 830.
Hence, the complete arithmetic pattern is 850, 400 845, 400 840, 400, 835, 400 830, 400.
Question 22.
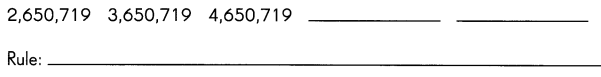
Answer: 5,650,719 6,650,719
It is an arithmetic pattern.
Definition: The arithmetic pattern is also known as the algebraic pattern. In an arithmetic pattern, the sequences are based on the addition or subtraction of the terms. If two or more terms in the sequence are given, we can use addition or subtraction to find the arithmetic pattern.
The given terms are 2,650,719 3,650,719 4,650,719 – – Now find the missing term in the sequence.
Here, we can use the addition process to figure out the missing terms in the patterns.
In the pattern, the rule used is “Add 1,000,000 to the previous term to get the next term”.
Now take the second term 3,650,719 If we add 1,000,000 to the second term (3,650,719), we get the third term (4,650,719).
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 4,650,719. Therefore, 4,650,719+1,000,000=5,650,719.
Second missing term: The previous term is 5,650,719. So, 5,650,719+1,000,000=6,650,719.
Hence, the complete arithmetic pattern is 2,650,719 3,650,719 4,650,719 5,650,719 6,650,719.
Question 23.

Answer:
It is an arithmetic pattern.
Definition: The arithmetic pattern is also known as the algebraic pattern. In an arithmetic pattern, the sequences are based on the addition or subtraction of the terms. If two or more terms in the sequence are given, we can use addition or subtraction to find the arithmetic pattern.
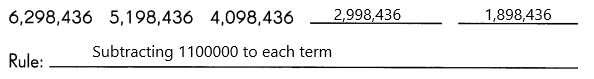
The given terms are 6,298,436 5,198,436 4,098,436 – – Now find the missing term in the sequence.
Here, we can use the subtraction process to figure out the missing terms in the patterns.
In the pattern, the rule used is “subtract 1,100,000 to the previous term to get the next term”.
Now take the second term 5,198,436 If we subtract 1,100,000 to the second term (5,198,436), we get the third term (4,098,436).
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 4,098,436. Therefore, 4,098,436-1,100,000=2,998,436.
Second missing term: The previous term is 2,998,436. So, 2,998,436-1,100,000=1,898,436.
Hence, the complete arithmetic pattern is 6,298,436 5,198,436 4,098,436 2,998,436 1,898,436.
Complete.
Question 24.
5,083,000 = 5,000,000 + ___ + 3,000 
Answer:80,000
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
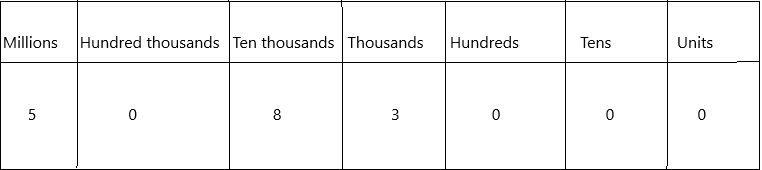
The value of digit for the given number 5,083,000:
: 5×1,000,000+0x100,000+8×10,000+3×1000+0x100+0x10+0x1
: 5,000,000+0+80,000+3000+0+0+0
: 5,000,000+80,000+3,000.
Question 25.
5,000,000 + 600,000 + 2,000 = ___ 
Answer: 5,602,000
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
The value of digit for the given number 5,602,000:
: 5×1,000,000+6×100,000+0x10,000+2×1000+0x100+0x10+0x1
: 5,000,000+600,000+0+2000+0+0+0
: 5,000,000+600,000+2,000.
The number is 5,602,000.
Question 26.
Which is greater, 509,900 or 562,000? ___ 
Answer: 562,000 is greater.
Explanation:
A whole number is larger than another if it has more digits. If the number of digits in each number is the same, then look at the digits from left to right. If the left digit is larger in one number, then this is the largest number. If this digit is the same, compare the next digit along to the right.
1. We are comparing the numbers 509,900 and 562,000
2. The order of digits from smallest to largest is 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
3. We start with the place value column on the left.
4. The hundred thousand place digits are the same in both numbers. Now compare the next digits.
5. 6 is greater than 0 because of the digits of the ten thousand place 0 and 6.
6. Therefore, 562,000 is greater than 509,900.
7. The comparison symbol for greater than is >, pointing to the less number of 509,900.
Question 27.
Which is less, 1,020,000 or 1,002,000? ___ 
Answer: 1,002,000 is less.
Here already asked which number is less than another number.
1. We are comparing the numbers 1,020,000 and 1,002,000.
2. The order of digits from smallest to largest is 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
3. We start with the place value column on the left.
4. The millions, hundred thousand place digits are the same in both numbers. Now compare the next digits.
5. 0 is less than 2 because the digits of the ten thousand place 0 and 2
6. Therefore, 1,002,000 is less than 1,020,000.
7. The comparison symbol for less than is <, pointing to the greater number of 1,020,000.
Question 28.
The value of the digit 1 in 7,1 20,000 is _100,000 and the place value is a hundred thousand.___ 
What goes around the world but remains in one corner? Write the letters that match the answers below to find out.
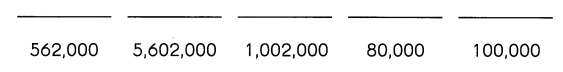
Answer: Stamp.
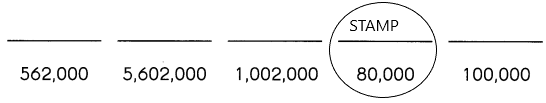
Why I choose 80,000:
Explanation:

For the given question the answer: stamp.
1. The stamp is having 5 letters.
2. In the given numbers check for the place values which is having up to 5 places.
3. Now check all the numbers and when coming to the 80,000, the place values are 8 in ten thousand, 0’s is in thousands, hundreds, tens and units place.
4. So, I think 80,000 will be the correct match to those 5 letters.
5. The five letters are ‘s’ ‘t’ ‘a’ ‘m’ ‘p’.
Read More:
BPCL Pivot Point Calculator