Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 9 Review Test to score better marks in the exam.
Math in Focus Grade 6 Course 1 B Chapter 9 Review Test Answer Key
Concepts and Skills
Use the coordinate plane below.
Question 1.
Give the coordinates of points A, B, C, D, and E.
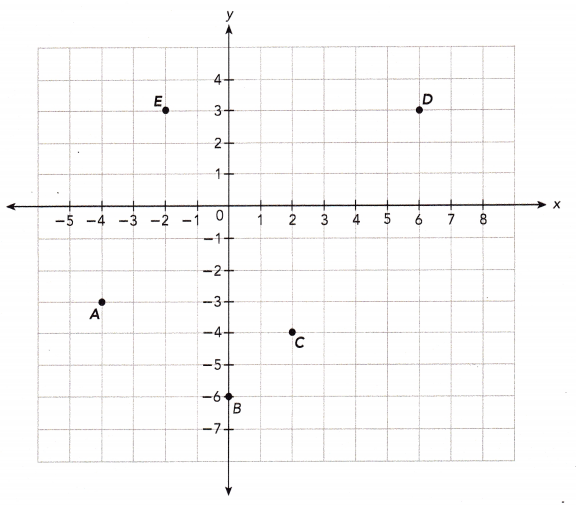
Answer:
Point A:
The first coordinate represents distance along negative x axis which is 4 and the second coordinate represents distance along negative y axis which is 3.
So, the point A will be (-4,-3)
Point B:
The first coordinate represents distance along x axis which is 0 and the second coordinate represents distance along negative y axis which is 6.
So, the point B will be (0,-6)
Point C:
The first coordinate represents distance along x axis which is 2 and the second coordinate represents distance along negative y axis which is 4.
So, the point C will be (2,-4)
Point D:
The first coordinate represents distance along x axis which is 6 and the second coordinate represents distance along y axis which is 3.
So, the point D will be (6,3)
Point E:
The first coordinate represents distance along the negative x axis which is 2 and the second coordinate represents distance along y axis which is 3.
So, the point E will be (-2,3)
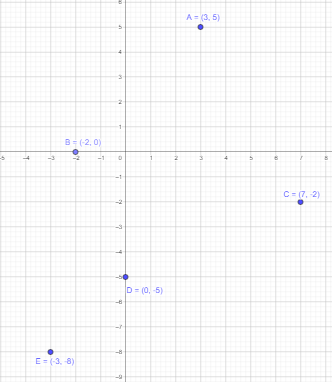
Use graph paper. Plot the points on a coordinate plane. In which quadrant is each point located?
Question 2.
A (3, 5), B (-2, 0), C (7, -2), D (0, -5), and E (-3, -8)
Answer:
Point A (3, 5): Since both the x and y coordinate are positive, the point A will be located in quadrant I.
Point B (-2, 0): Since the x coordinate is negative and y coordinate is origin, the point B will not lie in any quadrant. It will be located on x axis.
Point C (7, -2): Since the x coordinate is positive and y coordinate is negative, the point C will lie in quadrant IV.
Point D (0, -5): Since the x coordinate is zero and y coordinate is negative, the point D will not lie in any quadrant. It will be located on y axis.
Point E (-3, -8): Since both the x and y coordinate are negative, the point A will be located in quadrant III.
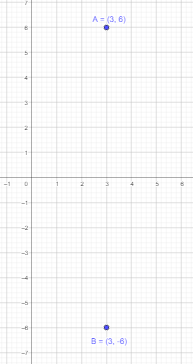
Use graph paper. Points A and B are reflections of each other about the x-axis. Give the coordinates of point B if the coordinates of point A are the following:
Question 3.
(3, 6)
Answer:
Given that the points A and B are reflections of each other about the x-axis.
Given that B is reflection of point A in the x-axis and point A is (3, 6).
If a point is reflected across the x-axis, The x-coordinate remains the same, but the y-coordinate is taken to be the additive inverse.
Thus, x coordinate will be 3 and y coordinate will be -6.
Therefore, point B will be (3,-6).
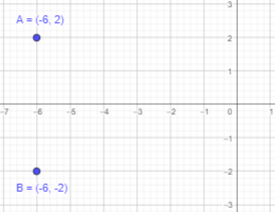
Question 4.
(-6, 2)
Answer:
Given that B is reflection of point A in the x-axis and point A is (-6, 2).
If a point is reflected across the x-axis, The x-coordinate remains the same, but the y-coordinate is taken to be the additive inverse.
Thus, x coordinate will be 3 and y coordinate will be -2.
Therefore, point B will be (-6,-2).
Question 5.
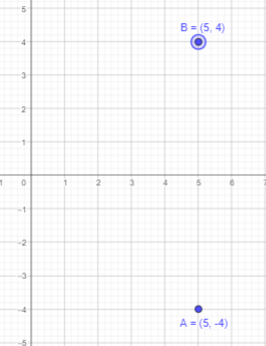
(5, -4)
Answer:
Given that B is reflection of point A in the x-axis and point A is (5, -4).
If a point is reflected across the x-axis, The x-coordinate remains the same, but the y-coordinate is taken to be the additive inverse.
Thus, x coordinate will be 5 and y coordinate will be 4.
Therefore, point B will be (5,4).
Question 6.
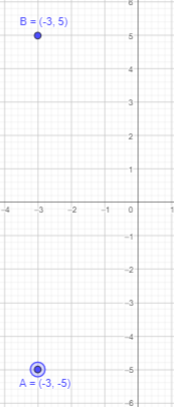
(-3, -5)
Answer:
Given that B is reflection of point A in the x-axis and point A is (-3, -5).
If a point is reflected across the x-axis, The x-coordinate remains the same, but the y-coordinate is taken to be the additive inverse.
Thus, x coordinate will be -3 and y coordinate will be 5.
Therefore, point B will be (-3,5).
Use graph paper. Points C and D are reflections of each other about the y-axis. Give the coordinates of point D if the coordinates of point C are the following:
Question 7.
(3, 6)
Answer:
Given that the points C and D are reflections of each other about the y-axis.
Given that C is reflection of point D in the y-axis and point C is (3, 6).
If a point is reflected across the y-axis, The x-coordinate is taken to be the additive inverse and the y-coordinate remains the same.
Thus, x cordinate will be -3 and y coordinate will be 6.
Therefore, point D will be (-3,6).

Question 8.
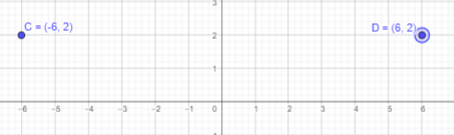
(-6, 2)
Answer:
Given that B is reflection of point A in the y-axis and point C is (-6, 2).
If a point is reflected across the y-axis, The x-coordinate is taken to be the additive inverse and the y-coordinate remains the same.
Thus, x cordinate will be 6 and y coordinate will be 2.
Therefore, point D will be (6,2).
Question 9.
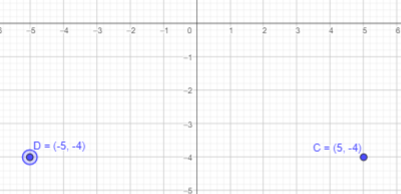
(5, -4)
Answer:
Given that B is reflection of point A in the y-axis and point C is (5, -4).
If a point is reflected across the y-axis, The x-coordinate is taken to be the additive inverse and the y-coordinate remains the same.
Thus, x cordinate will be -5 and y coordinate will be -4.
Therefore, point D will be (-5,-4).
Question 10.
(-3, -5)
Answer:
Given that B is reflection of point A in the y-axis and point C is (-3, -5).
If a point is reflected across the y-axis, The x-coordinate is taken to be the additive inverse and the y-coordinate remains the same.
Thus, x cordinate will be 3 and y coordinate will be -5.
Therefore, point D will be (3,-5).
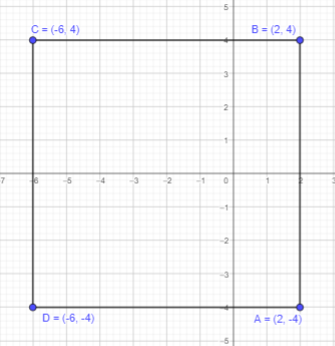
Use graph paper. For each exercise, plot the given points on a coordinate plane. Then connect the points in order with line segments to form a closed figure. Name each figure formed.
Question 11.
A (2, -4), B (2, 4), C (-6, 4), and D (-6, -4)
Answer:
Plot the points A,B,C and D on a coordinate plane. Connect the points in order with line segments to form a closed figure.
The formed figure has all equal sides. Therefore, it can be a square.
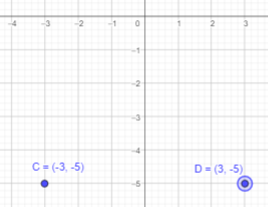
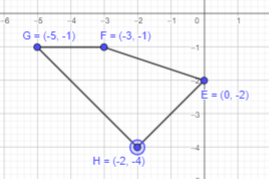
Question 12.
E (0, -2), F (-3, 1), G(-5, -1), and H (-2, -4)
Answer:
Plot the points E,F,G and H on a coordinate plane. Connect the points in order with line segments to form a closed figure.
The formed figure has all four sides different. Therefore, it can be a quadrilateral.
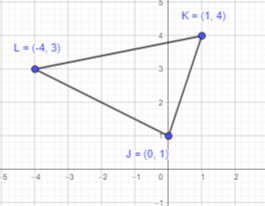
Question 13.
J (0, 1), K(1, 4), and L(-4, 3)
Answer:
Plot the points J,K and L on a coordinate plane. Connect the points in order with line segments to form a closed figure.
The formed figure has all three sides different. Therefore, it can be a triangle.
Question 14.
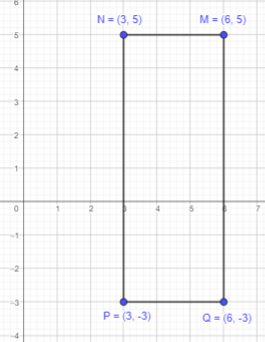
M (6, 5), N (3, 5), P (3, -3), and Q (6, -3)
Answer:
Plot the points M,N,P and Q on a coordinate plane. Connect the points in order with line segments to form a closed figure.
The formed figure has opposite sides equal. Therefore, it can be a rectangle.
Question 15.
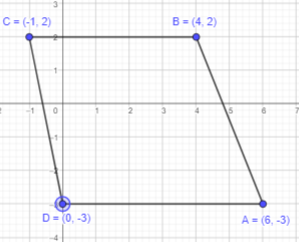
A (6, -3), B (4, 2), C (-1, 2), and D (0, -3)
Answer:
Plot the points A,B,C and D on a coordinate plane. Connect the points in order with line segments to form a closed figure.
The formed figure has a pair of opposite sides parallel and equal. Therefore, it can be a parallelogram.
Question 16.
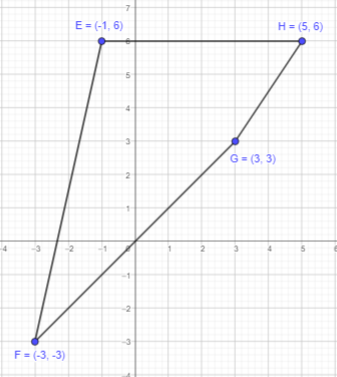
E (-1, 6), F (-3, 3), G (3, 3), and H (5, 6)
Answer:
Plot the points E,F,G and H on a coordinate plane. Connect the points in order with line segments to form a closed figure.
The formed figure has all different sides. Therefore, it can be a quadrilateral.
Question 17.
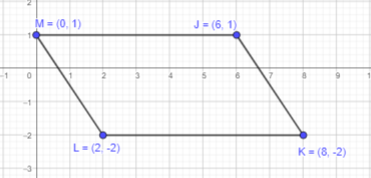
J(6, 1), K(8, -2), L (2, -2), and M (0, 1)
Answer:
Plot the points J,K,L and M on a coordinate plane. Connect the points in order with line segments to form a closed figure.
The formed figure has a pair of opposite sides parallel and equal. Therefore, it can be a parallelogram.
Question 18.
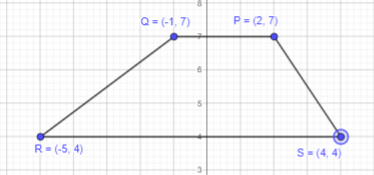
P (2, 7), Q (-1, 7), R (-5, 4), and S (4, 4)
Answer:
Plot the points P,Q,R and S on a coordinate plane. Connect the points in order with line segments to form a closed figure.
The formed figure has a pair of opposite sides parallel and equal. Therefore, it can be a trapezium.
Question 19.
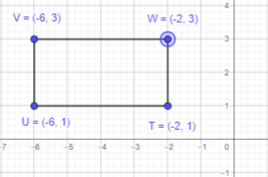
T (-2, 1), U (-6, 1), V(-6, -3), and W(-2, -3)
Answer:
Plot the points T,U,V and W on a coordinate plane. Connect the points in order with line segments to form a closed figure.
The formed figure has opposite sides equal. Therefore, it can be a rectangle.
Use graph paper. Plot the points on a coordinate plane and answer the question.
Question 20.
a) Plot points A (1, -1) and B (7, -1) on a coordinate plane. Connect the two points to form a line segment.
Answer:
Point A:
The first coordinate represents distance along positive x axis which is 1 and the second coordinate represents distance along negative y axis which is 1.
So, the point A will be (1,-1)
Point B:
The first coordinate represents distance along positive x axis which is 7 and the second coordinate represents distance along negative y axis which is -1.
So, the point A will be (7,-1)

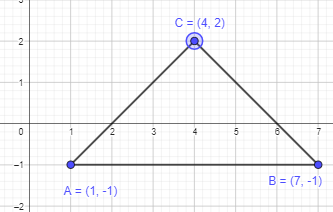
b) Point C lies above \(\overline{\mathrm{AB}}\), and is 2 units away from the x-axis. If triangle ABC is an isosceles triangle with base \(\overline{\mathrm{AB}}\), find the coordinates of point C.
Answer:
Point C lies above \(\overline{\mathrm{AB}}\), and is 2 units away from the x-axis. If triangle ABC is an isosceles triangle with base \(\overline{\mathrm{AB}}\)
Since it is an isosceles triangle, two sides will be equal. When the line segment is joined through midpoint, the formed line segments will be equal in length.
Midpoint of AB line segment is 3 units, so midpoint will be (4,2).
Thus, coordinates of point C will be (4,2)
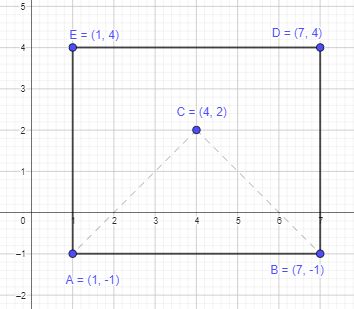
c) Points D and E lie below \(\overline{\mathrm{AB}}\) such that ABDE is a rectangle. If BD is 5 units, find the coordinates of points D and E.
Answer:
Given that BD is 5 units.
Points D and E lie below \(\overline{\mathrm{AB}}\) such that ABDE is a rectangle.
Start from point B and move 5 units above and mark it. Thus, the required point D will be formed.
Since it is a rectangle, opposite sides will be equal. Therefore, AB will be equal to DE, which is 6 units.
Start from point D and move 6 units towrads left and mark it is as E.
Thus, the formed D point will be (7,4) and E will be (1,4).
Use graph paper. Plot each pair of points on a coordinate plane. Connect the points to form a line segment and find its length.
Question 21.
A (-1,0) and B (8, 0)
Answer:
To plot point A (-1,0):
Here, the x-coordinate of A is -1 and the y-coordinate is 0. Start at the Origin. As the x coordinate is negative, move 1 units on the negative x-axis and point it.
Thus, the required point (-1,0) is marked.
To plot point B (8, 0):
Here, the x-coordinate of A is 8 and the y-coordinate is 0. Start at the Origin. As the x coordinate is positive, move 8 units along the positive x-axis and point it.
Thus, the required point B (8, 0) is marked.
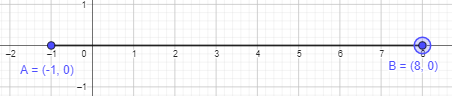
After connecting the points to form a line segment, the length will be 9 units.
Question 22.
C (-2, 4) and D (6, 4)
Answer:
To plot point C (-2, 4):
Here, the x-coordinate is -2 and the y-coordinate is 4. Start at the Origin. As the x coordinate is negative, move 2 units on the negative x-axis and 4 units on the positive y -axis.
Thus, the required point C (-2,4) is marked.
To plot point D (6, 4):
Here, the x-coordinate is 6 and the y-coordinate is 4. Start at the Origin. As the x coordinate is positive, move 4 units along the positive x-axis and 4 units along positive y -axis.
Thus, the required point D (6, 4) is marked.
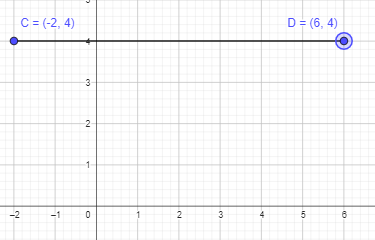
After connecting the points to form a line segment, the length will be 8 units.
Question 23.
E (-6, -2) and F(-6, -6)
Answer:
To plot point E (-6, -2):
Here, the x-coordinate is 6 and the y-coordinate is-2. Start at the Origin. As the x coordinate is negative, move 6 units on the negative x-axis and 2 units on the negative y -axis.
Thus, the required point C (-2,4) is marked.
To plot point F(-6, -6):
Here, the x-coordinate is -6 and the y-coordinate is -6. Start at the Origin. As the x coordinate is negative, move 6 units along the negative x-axis and 6 units along negative y -axis.
Thus, the required point D (-6, -6) is marked.
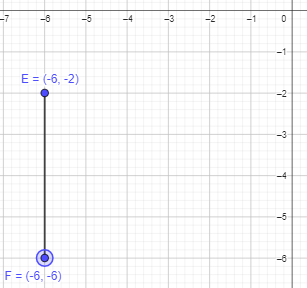
After connecting the points to form a line segment, the length will be 4 units.
Question 24.
G (-5, -4) and H (2, -4)
Answer:
To plot point G (-5, -4):
Here, the x-coordinate is -5 and the y-coordinate is-4. Start at the Origin. As the x coordinate is negative, move 5 units on the negative x-axis and 4 units on the negative y -axis.
Thus, the required point G (-5, -4) is marked.
To plot point H (2, -4):
Here, the x-coordinate is 2 and the y-coordinate is -4. Start at the Origin. As the x coordinate is positive, move 4 units along the positive x-axis and 4 units along negative y -axis.
Thus, the required point H (2, -4) is marked.
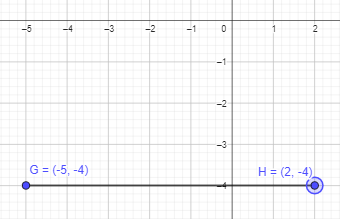
After connecting the points to form a line segment, the length will be 7 units.
Question 25.
J(0, -3) and K(0, -8)
Answer:
To plot point J(0, -3):
Here, the x-coordinate is 0 and the y-coordinate is-3. Start at the Origin. As the x coordinate is origin, move 3 units on the negative y -axis.
Thus, the required point J(0, -3) is marked.
To plot point K(0, -8):
Here, the x-coordinate is 0 and the y-coordinate is-8. Start at the Origin. As the x coordinate is origin, move 8 units on the negative y -axis.
Thus, the required point K(0, -8) is marked.
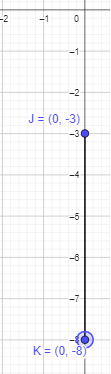
After connecting the points to form a line segment, the length will be 5 units.
Question 26.
M (5, 2) and N (5, -5)
Answer:
To plot point M (5, 2):
Here, the x-coordinate is 5 and the y-coordinate is 2. Start at the Origin. As the x and y coordinates are positive , move 5 units on the positive x-axis and 2 units on the positive y -axis.
Thus, the required point M (5, 2) is marked.
To plot point N (5, -5):
Here, the x-coordinate is 5 and the y-coordinate is 5. Start at the Origin. Move 5 units on the positive x-axis and 2 units on the negative y -axis.
Thus, the required point N (5, -5) is marked.
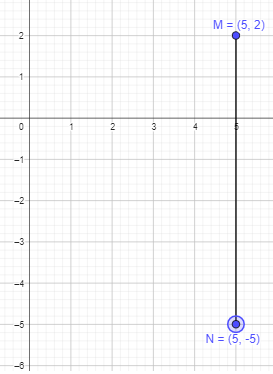
After connecting the points to form a line segment, the length will be 7 units.
Problem Solving
The diagram shows the plan of a room. The side length of each grid square is 10 feet. Use the diagram to answer questions 27 to 28.
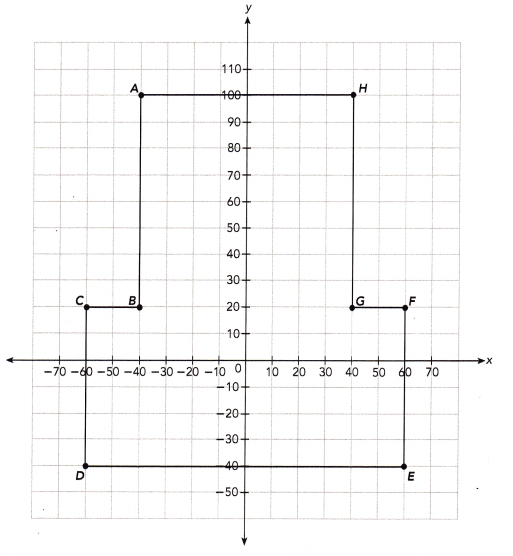
Question 27.
The eight corners of the room are labeled points A to H. Give the coordinates of each of these corners.
Answer:
The first coordinate represents distance along negative x axis which is 40 and the second coordinate represents distance along y axis which is 100.
The coordinates of A will be (-40,100)
Similarly,The coordinates of B will be (-40,20)
The coordinates of C will be (-60,20)
The coordinates of D will be (-60,-40)
The coordinates of E will be (60,40)
The coordinates of F will be (60,20)
The coordinates of G will be (40,20)
The coordinates of H will be (40,100)
Question 28.
The entrance of the room is situated along \(\overline{\mathrm{AH}}\). What is the shortest possible distance in feet between the entrance and \(\overline{\mathrm{DE}}\) of the room?
Answer:
The entrance of the room is situated along \(\overline{\mathrm{AH}}\).
The shortest distance between the the entrance and \(\overline{\mathrm{DE}}\) of the room will be the straight route from AH to DE.
The distance between AH to DE is 14 square grids.
Each square grid equals to 10 feet.
Thus, the distance between AH to DE will be 14×10 = 140 ft.
Question 29.
Diana walks across the room from point B to point G, and then walks from point G to point H. Find the total distance, in feet, that Diana walks.
Answer:
Given that Diana walks across the room from point B to point G, and then walks from point G to point H.
Distance between B and G will be 8 square grids, 8×10=80 ft.
Distance between G to H will be 8 square grids, 8×10=80 ft.
The total distance will be BG+GH = 80+80 = 160 ft
Question 30.
Calculate the floor area of the room in square feet.
Answer:
As the complete floor area is in irregular shape, we will find the area in parts.
To calculate the floor area, we will find the area of rectangle AHGB and area of CFED
Area of rectangle AHGB:
Length of AB will be 8 square grids, 8×10=80 ft.
Length of AH will be 8 square grids, 8×10=80 ft.
Area of the rectangle = length×width
= 80×80
= 6400 sq.ft
Area of rectangle CFED:
Length of CD will be 6 square grids, 6×10=60 ft.
Length of DE will be 12 square grids, 12×10=120 ft
Area of the rectangle = length×width
= 60×120
= 7200 sq.ft
Thus, the total area of floor will be 6400+7200 = 13600 sq.ft
Use graph paper. Solve.
Question 31.
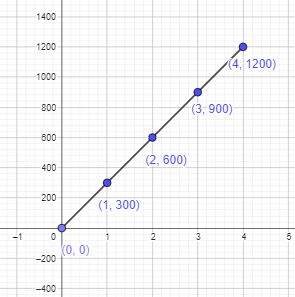
An athlete took part in a race. The distance the athlete ran, v meters, after t minutes, is given by v = 300t. Graph the relationship between t and v. Use 2 units on the horizontal axis to represent 1 minute and 1 unit on the vertical axis to represent 150 meters.

a) What type of graph is it?
Answer:
It is a straight line graph.This is also called a linear graph.
b) What is the distance the athlete ran in 3.5 minutes?
Answer:
An athlete took part in a race. The distance the athlete ran, v meters, after t minutes, is given by v = 300t.
Here, t=3.5 min
v = 300t
v = 300×3.5
= 1050 m
Thus the distance the athlete ran in 3.5 min will be 1050 m.
c) What is the average speed of the athlete?
Answer:
The average speed of the athlete will be,
Average speed = \(\frac{total distance}{total time}\)
Total distance will be 0+300+600+900+1200 = 3000 m
Total time will be 0+1+2+3+4 = 10 min
= \(\frac{3000}{10}\)
= 300 meters per min
d) Assuming the athlete runs at a constant speed, what is the distance she will run in 8 minutes?
Answer:
The distance the athlete ran, v meters, after t minutes, is given by v = 300t.
The distance she will run in 8 min will be, 300×8=2400 m
e) Name the dependent and independent variables.
Answer:
From the graph, we can say v is the dependent variable and t is the independent variable.
Question 32.
A truck uses 1 gallon of diesel for every 12 miles traveled, The amount of diesel left in the gas tank, r gallons, after traveling s miles is given by s = 300 – 12r. Copy and complete the table. Graph the relationship between r and s. Use 1 unit on the horizontal axis to represent 1 gallon and 1 unit on the vertical axis to represent 12 miles. Start your horizontal axis at 17 gallons.
a)

Answer:
A truck uses 1 gallon of diesel for every 12 miles traveled, The amount of diesel left in the gas tank, r gallons, after traveling s miles is given by s = 300 – 12r.
Here s=24,
24 = 300 – 12r
24+12r = 300-12r+12r
24+12r = 300
24+12r-24 = 300-24
12r = 276
r = 276÷12 = 23 gallons
Here r=17,
s = 300 – 12×17
= 300-204
= 96 miles

b) How many gallons of diesel are left after the truck has traveled 60 miles?
Answer:
If 60 miles is travelled,
s = 300 – 12r
60 = 300 – 12r
60 + 12r = 300 – 12r + 12r
60 + 12r = 300
60 + 12r – 60 = 300-60
12r = 240
12r÷12 = 240÷12
r = 20
Thus, 20 gallons of diesel are left after the truck has traveled 60 miles
c) After the truck has traveled for 72 miles, how much farther can the truck travel before it runs out of diesel?
Answer:
After 72 miles, 19 gallons of gas were left.
Distance = 19 × mileage
72 = 19×mileage
72÷19 = (19×mileage)÷19
3.7 = mileage
The car can travel another 3.7 miles
d) If the truck travels more than 48 miles, how much diesel is left in the gas tank? Express your answer in the form of an inequality in terms of r, where r stands for the amount of diesel left.
Answer:
If the truck travels more than 48 miles, r ≥ 21, where r stands for the amount of diesel left.