Math in Focus Grade 5 Cumulative Review Chapters 11 to 13 Answer Key

This handy Math in Focus Grade 5 Workbook Answer Key Cumulative Review Chapters 11 to 13 provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Cumulative Review Chapters 11 to 13 Answer Key

Concepts and Skills

• Angles next to each other sum up to 180°

• Opposite angles are equal.

The double bar graph shows the number of pairs of black jeans and blue jeans produced in a factory in three days.

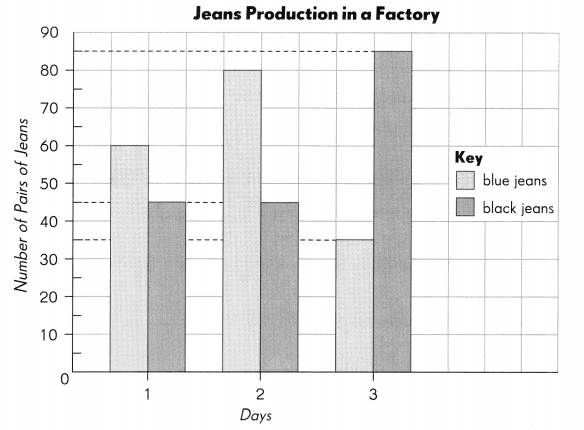
Complete. Use the data in the graph on page 145. (Lesson 11.1)

Question 1.
On day 2, ___ more pairs of blue jeans thon black jeans are produced.
Answer: 35.
Explanation:
On day 2, 35 more pairs of blue jeans than black jeans are produced.
80 – 45 = 35

Question 2.
On day ___ and day ___, the same number of pairs of black jeans are produced.
Answer:
Day 1 and 2
Explanation:
On day 1 and day 2 , the same number of pairs of black jeans are produced.

Question 3.
The greatest number of blue jeans is produced on day ____.
Answer:
Day 2
Explanation:
The greatest number of blue jeans is produced on day 2.
That is 80

Question 4.
On day 1, the difference between the number of pairs of blue jeans and black jeans produced is ___.
Answer: 15
Explanation:
On day 1, the difference between the number of pairs of blue jeans and black jeans produced is 15.
60 – 45 = 15

Question 5.
The total number of pairs of jeans produced in the three days is ___.
Answer: 350
Explanation:
The total number of pairs of jeans produced in the three days is 350.
60 + 45 = 105
80 + 45 = 125
35 + 85 = 120
105 + 125 + 120 = 350

Question 6.
The ratio of the number of pairs of block jeans produced to the number of pairs of blue jeans produced on day 3 is ____.
Answer: 17 : 7
Explanation:
The ratio of the number of pairs of block jeans produced to the number of pairs of blue jeans produced on day 3 is 17 : 7.
85 : 35 = 17 : 7

Question 7.
Express the number of black jeans produced on doy 1 as a fraction of the number of blue jeans produced on day 1. ___________
Answer: \(\frac{4}{3}\)
Explanation:
The number of black jeans produced on doy 1 as a fraction of the number of blue jeans produced on day 1. \(\frac{4}{3}\)
60 ÷ 45 = \(\frac{4}{3}\)

Question 8.
Express the total number of blue jeans produced as a percent of the total number of jeans produced in the three days. ____
Answer:
The total number of blue jeans produced as a percent of the total number of jeans produced in the three days. \(\frac{1}{2}\)
Explanation:
60 + 80 + 35 = 175
total number of jeans produced in the three days. = 350
\(\frac{1}{2}\)

Each solid is cut vertically along the line shown. Identify the solid shapes that result.

Explanation:

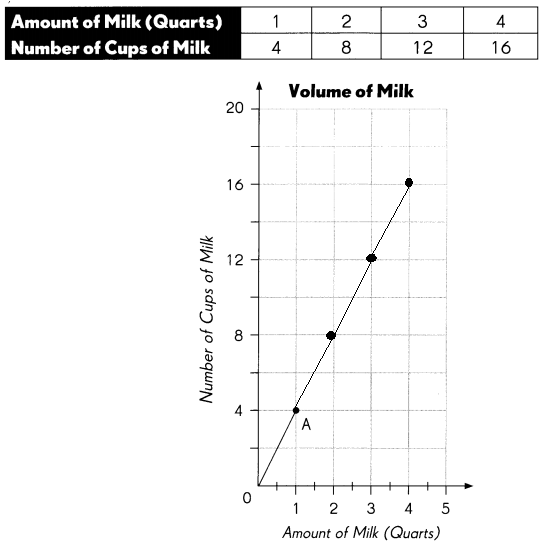
Question 9.
What are the coordinates of point A? ____
Answer:
1 and 4
Explanation:
1 and 4 are the coordinates of point A

Question 10.
How many quarts of milk are in 12 cups? ____
Answer:
3 quarts
Explanation:
3  quarts of milk are in 12 cups

Question 11.
How many cups of milk are in 3\(\frac{1}{2}\) quarts of milk?
Answer:
3\(\frac{1}{2}\) = 15 quarts
Explanation:
3\(\frac{1}{2}\) = 15 quarts
15 quarts of milk

Question 12.
How many cups of milk are in 5 quarts of milk? ___
Answer:
5 = 20 quarts
Explanation:
20 cups of milk are in 5 quarts of milk

Make an organized list to find the number of combinations. (Lesson 11.3)

Barry’s Yogurt Shop sells frozen yogurt with a topping. A customer can pick one of three flavors: vanilla, strawberry, and blueberry. The customer can pick one of three toppings: nuts, raisins, and sprinkles.

Question 13.
List all the possible combinations of yogurt flavor and topping.

Answer: 9 possibilities
Explanation:

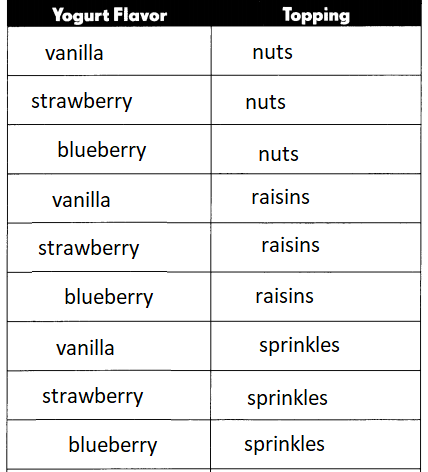
Find the number of combinations. (Lesson 11.3)
Question 14.
Brenda has 1 red, 1 green and 1 gold bracelet. She has 4 pairs of earrings: stud, hoop, button, and dangling. She wants to find all the combinations of 1 bracelet and 1 pair of earrings that she can wear.
Answer:
12
Explanation:
She can wear 12 combinations

Question 15.
Draw a tree diagram to show the possible combinations.
Answer:

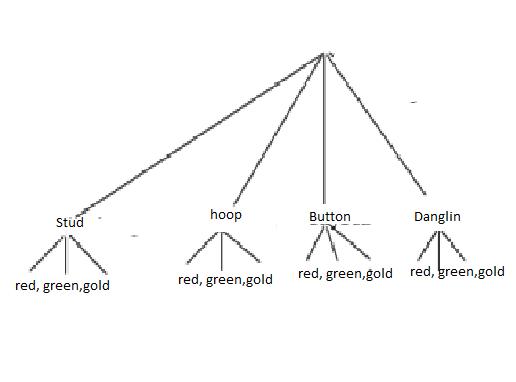
Explanation:
Tree diagram is shown above for possible combinations
4 x 3 = 12

Question 16.
Find the number of combinations by multiplication.
____ × ____ = ____
There are ___ combinations.
Answer:
4 x 3 = 12
There are 12 combinations.

Complete. (Lesson 11.4)

A bag has 5 green toothbrushes and 7 yellow toothbrushes. Tim and Cathy each pick a toothbrush, and then return it to the bag. They do this for 20 times each. The table shows some of their results.

Question 17.
Complete the table.

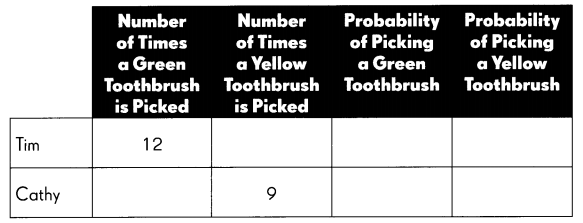
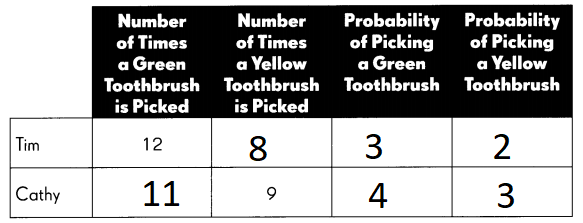
Answer:

Question 18.
The theoretical probability of picking a yellow toothbrush is ____.
Answer:
The theoretical probability of picking a yellow toothbrush is 2

Question 19.
The experimental probability of picking a green toothbrush that Tim’s results show is ____________
Answer:
The experimental probability of picking a green toothbrush that Tim’s results show is 3

Find the unknown angle measures. (Lesso 12.1)

Question 20.
\(\overleftrightarrow{A B}\) is a line.

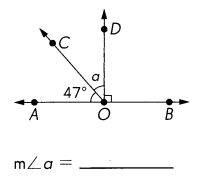
Answer:
∠AOD = 43°
Explanation:
∠AOD = 90°
∠AOC = 47°
90 – 47 = 43°

Question 21.
\(\overleftrightarrow{A B}\) is a line. The measures of ∠a, ∠b, and ∠c are equal.

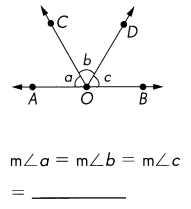
Answer:
m∠a = 60°
m∠b = 60°
m∠c = 60°
Explanation:
∠AOD = 180°
180 ÷ 3 = 60°

Find the unknown angle measures. (Lesson 12.1 and 12.2)

Question 22.
\(\overleftrightarrow{A B}\) is a line.

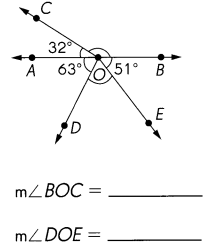
Answer:
∠BOC = 148°
∠DOE = 66°
Explanation:
∠AOB = 180°
∠AOC = 32°
180 – 32 = 148°
∠AOD = 63°
∠BOE =51°
∠AOB =180°
63 + 51 = 114
180 – 114 = 66
∠DOE = 66°

Question 23.
\(\overleftrightarrow{A B}\) is a line.

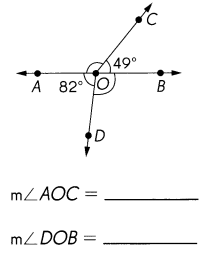
Answer:
m∠AOC = 131°
m∠BOD = 98°
Explanation:
∠AOB = 180°
∠BOC = 49°
180 – 49 = 131°
∠AOD = 82°
∠AOB =180°
180 – 82 = 98
∠BOD = 98°

Question 24.

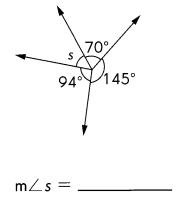
Answer: m∠s = 51°

Explanation:
Complete angle = 360°
So m∠s =  360° – 145 ° + 94 ° +70°= 51°

Question 25.

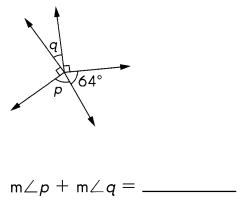
Answer:  m∠p + m∠q  =116°
Explanation:
Complete angle = 360°
So m∠p + m∠q  = 360° – 64° + 90° +90° =116°

Question 26.

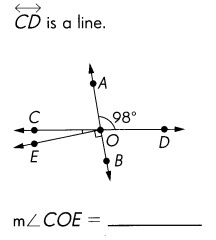
Answer: 8°
Explanation:
m∠COD= 180°
m∠COA= 180° – 98° = 82°
if AB is line
m∠BOA = 180°
m∠BOE= 90°
m∠COA = 82°
m∠COE= 180° – 98° + 82° =8°

Question 27.

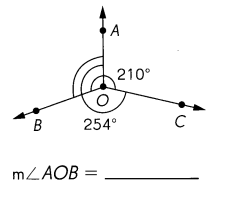
Answer: m∠AOB= 104°
Explanation:
m∠BOA + m∠AOC = 210°
m∠COB + m∠BOA= 254°
Complete angle =360°
m∠AOC= 360° – m∠COB + m∠BOA=360°- 254° =106°
m∠BOC= 360°-m∠BOA + m∠AOC  = 360°- 210° =150°
m∠AOB =  360°-m∠AOC + m∠BOC = 360° – 150° + 106° =104°

Find the unknown angle measures. (Lesson 13.3)

\(\overleftrightarrow{A B}\), \(\overleftrightarrow{C D}\) and \(\overleftrightarrow{E F}\) are lines.

Question 28.

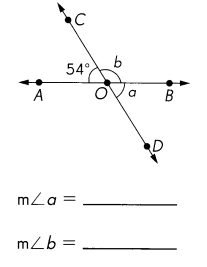
Answer:
m∠a =54 °
m∠b =126 °
Explanation:
\(\overleftrightarrow{A B}\) is line, So m∠BOA = 180 ° then
m∠b = 180 ° – m∠AOC  = 180 ° – 54° =126 °
\(\overleftrightarrow{C D}\) is line, So m∠COD= 180 ° then
m∠a = 180 ° – m∠b = 180 ° – 126° =54 °

Question 29.

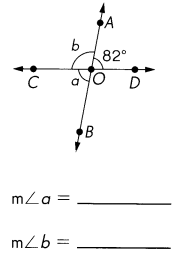
Answer:
m∠a= 180 ° – m∠DOB= 180 ° -82° = 98 °
m∠b=  m∠DOA= 82°
Explanation:
Intersecting lines create two pairs of vertical angles which are congruent.  Furthermore, intersecting lines create adjacent angles that are supplementary (sum to 180 degrees)
m∠COD= 180 °
m∠a= 180 ° – m∠DOB= 180 ° -82° = 98 °
Vertical angles are always congruent, which means that they are equal.
m∠b=  m∠DOA= 82°

Question 30.

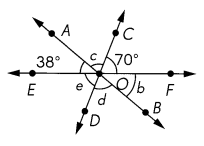
m∠b = ___
m∠c = ___
m∠d = ___
m∠e = ___
m∠b + m∠d + m∠e
= ____
Answer:
m∠b = m∠EOA =38°
m∠c = 180 ° – m∠EOA +m∠COF = 180 ° – 38° +70° =72°
m∠d = m∠c =72°
m∠e = m∠COF =70°
m∠b + m∠d + m∠e = 180 °
Explanation:
Intersecting lines create two pairs of vertical angles which are congruent.  Vertical angles are always congruent, which means that they are equal. Furthermore, intersecting lines create adjacent angles that are supplementary (sum to 180 degrees)
m∠EOF= 180 °
m∠c = 180 ° – m∠EOA +m∠COF = 180 ° – 38° +70° =72°
m∠b = m∠EOA =38°
m∠c = 72°
m∠d = m∠c =72°
m∠e = m∠COF =70°
m∠b + m∠d + m∠e = 180 °

Question 31.

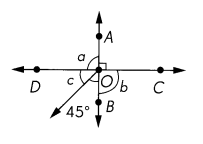
m∠a = ___
m∠b = ___
m∠c = ___
Answer:
m∠a = 90°
m∠b = 90°
m∠c = 45°
Explanation:
Intersecting lines create two pairs of vertical angles which are congruent.  Vertical angles are always congruent, which means that they are equal. Furthermore, intersecting lines create adjacent angles that are supplementary (sum to 180 degrees)
m∠a =  180 °  – m∠COA  = 180 °  – 90° = 90°
m∠b = 180 °  – m∠COA  = 180 °  – 90° = 90°
m∠DOB = 90°
m∠c  =m∠DOB  – 45° = 90°  – 45° = 45°

Find the unknown angle measures. Then classify triangle ABC as an acute, obtuse, or right triangle. (Lessons 13.1 to 13.3)

Question 32.

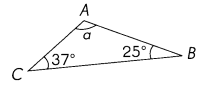
m∠a = ____
___ triangle
Answer:
m∠a = 118°
Obtuse triangle
Explanation:
The three interior angles of a triangle will always have a sum of 180°.
m∠a  =180 ° –  m∠ABC+ m∠DOB  = 180°- 37°  + 25 ° = 118°
An obtuse triangle is a triangle with one angle that is greater than 90 degrees.
118°>90°. So it is Obtuse triangle

Question 33.

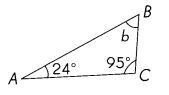
m∠b = ____
___ triangle
Answer:
m∠b = 64°
Obtuse triangle

Explanation:
The three interior angles of a triangle will always have a sum of 180°.
m∠b  =180 ° –  m∠ACB+ m∠BAC= 180°- 95°  + 24° = 64°
An obtuse triangle is a triangle with one angle that is greater than 90 degrees.
118°>90°. So it is Obtuse triangle

Question 34.

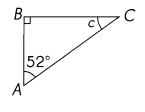
m∠c = ____
___ triangle
Answer:
m∠c = 38°
right triangle
Explanation:
The three interior angles of a triangle will always have a sum of 180°.
m∠b  =180 ° –  m∠BAC+ m∠ABC= 180°- 52°  + 90° = 38°
A right triangle is a triangle with one 90 degree angle.
m∠ABC= 90°. So it is right triangle

Question 35.

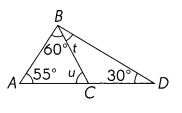
m∠u = ____
m∠t = ____
___ triangle
Answer:
m∠u = 65°
m∠t = 35°
ABD is Obtuse  triangle
ABC is acute triangle
Explanation:
The three interior angles of a triangle will always have a sum of 180°.
m∠u  =180 ° –  m∠BAC+ m∠ABC= 180°- 55°  + 60° = 65°
m∠BAD+ m∠ABD + m∠ADB = 180°
m∠ABD= 180° – m∠BAD + m∠ADB
m∠ABD= 180° – 55° + 30 =95°
m∠t = m∠ABD – m∠ABC= 95°-60°=35°
An obtuse triangle is a triangle with one angle that is greater than 90 degrees.
m∠ABD = 95°. So it is Obtuse triangle

Question 36.

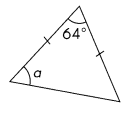
m∠a = ____
Answer:
m∠a =  58°
Explanation:
The three interior angles of a triangle will always have a sum of 180°. and
Remaining sum of two angles  = 180° – 64° =116°.
The isosceles triangle theorem further states that the angles opposite to each of the equal sides must also be equal.
So m∠a = 116° divide by 2 = 58°

Question 37.

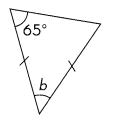
m∠b = ____
Answer:
m∠b = 50°
Explanation:
The isosceles triangle theorem further states that the angles opposite to each of the equal sides must also be equal.
one angle is 65° so it is isosceles triangle then opposite angle also 65°
The three interior angles of a triangle will always have a sum of 180°. then
m∠b = 180° – 65° + 65°=50°

Question 38.
AB = BC = AD

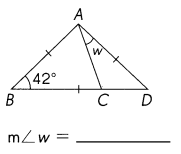
Answer:
m∠w = 27°
Explanation:
in Triangle ABC
m∠BAC+ m∠BCA = 180° –  m∠ABC = 180 – 42 =138
The isosceles triangle theorem further states that the angles opposite to each of the equal sides must also be equal.
m∠BAC = m∠BCA =138 divide by 2 =69°
in Triangle ABD
m∠ABD= m∠ADB =42°
The isosceles triangle theorem further states that the angles opposite to each of the equal sides must also be equal.
So m∠BAD = 180 – 84 =96°
m∠w = 96° – 69° =27°

Question 39.

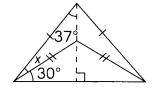
m∠x = ____
Answer: m∠x = 23°

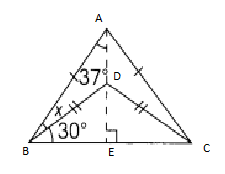
Explanation:
m∠CEA= m∠BEA= 90°
in Triangle BEA
m∠ABE= 180  – m∠BAE+ m∠BEA= 180 – 37 +90° =  53°
m∠x  =m∠ABE  –  30° = 53- 30=23°

Find the unknown angle measures. (Lesson 13.3)

Question 40.

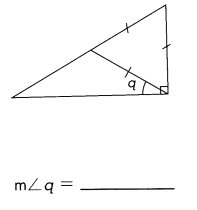
Answer:

Explanation:
m∠ABC= 90° given
Triangle ADB is equilateral triangle – All three sides are equal. All three angles are congruent and are equal to 60 degrees.
m∠ABD =  60°
m∠a= m∠ABC- m∠ABD=90- 60=30°

Question 41.
ZY = YX = XZ

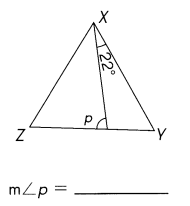
Answer:

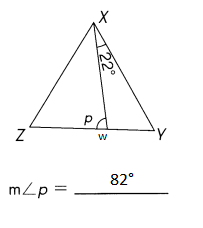
Explanation:
ZY = YX = XZ So Triangle XYZ is equilateral triangle – All three sides are equal. All three angles are congruent and are equal to 60 degrees.
So m∠ZXY= m∠XZY=  60°
So m∠WXZ = 60 – 22 = 38
m∠ p = 180 – 38 + 60 =82°

Measure the sides of the triangles in inches. Then fill in the blanks. (Lessons 13. 1 and 13.4)

Explanation:

Question 42.
AB is ___________ inches.
Answer:
AB is 3 inches.

Question 43.
BC is ___________ inches.
Answer:
BC is 5 inches.

Question 44.
AC is _________ inches.
Answer:
AC is 3 inches.

Question 45.
AB + BC > _______
Answer:
AB + BC
3 + 5 = 8
AB + BC > AC
AC = 3

Question 46.
AB + AC > ________
Answer:
AB + AC > BC
AB = 3
BC = 5
AC = 3
3 + 3 = 6
6 > 5

Question 47.
BC + AC > ________
Answer:
BC + AC >  AB
BC = 5
AC = 3
3 + 5 = 8
AB = 3
8 > 3

Question 48.
What kind of triangle is ABC? ____
Answer:
Isosceles. An isosceles triangle can be drawn in many different ways. It can be drawn to have two equal sides and two equal angles or with two acute angles and one obtuse angle.

Find the unknown angle measures in each parallelogram. (Lesson 13.5)

Question 49.

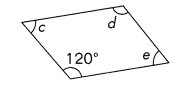
m∠c = ___
m∠d = ___
m∠e = ___
Answer:
m∠c = 60 °
m∠d = 120°
m∠e = 60 °
Explanation:

Question 50.

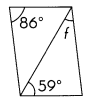
m∠f = ___
Answer:

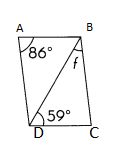
m∠f = 35°
Explanation:
Opposite angles are equal in Parallelogram  So m∠BCD = 86°
In Triangle BCD, m∠BCD = 86° and m∠BDC= 59°
m∠f= 180-86°+59 = 35°

Find the unknown angle measures in each rhombus. (Lesson 13.5)

Question 51.

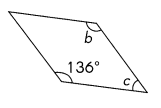
m∠b = ___
m∠c = ___
Answer:
m∠b = 136°
m∠c = 44°
Explanation:
Opposite angles are equal in rhombus So m∠b = 136°
Sum of any two adjacent angles is 180°. So m∠b + m∠c = 180°
then  m∠c = 180° – m∠b = 180 -136 =44°

Question 52.

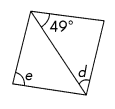
m∠d = ___
m∠e = ___
Answer:

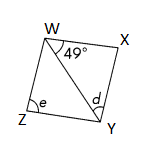
m∠d = 49°
m∠e = 82°
Explanation:
In Rhombus, All sides are equal and, opposite sides are parallel to each other.

\(\overline{W X}\) = \(\overline{X Y}\)  = \(\overline{Y Z}\) =\(\overline{Z W}\)
So WXY is isosceles  triangle. So m∠XWY = m∠XYW = m∠d= 49°
Then m∠WXY = 180 – 49 + 49 =82°

In Rhombus, Opposite angles are equal.
m∠e= 82°

Find the unknown angle measures in each trapezoid. (Lesson 13.5)

Question 53.
In EFGH, \(\overline{E F}\) || \(\overline{H G}\).

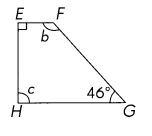
m∠b = ___
m∠c = ___
Answer:
m∠b =134°
m∠c = 90°
Explanation:
A right trapezoid also called the right-angled trapezoid, has a pair of right angles.
So m∠c = 90°
m∠b = 360 – 90 + 90 +49 =134°

Question 54.
In PQRS, \(\overline{P S}\) || \(\overline{Q R}\).

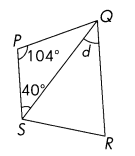
m∠d = ___
Answer:
m∠d = 104°
Explanation:
In Triangle PQS,
m∠PQS =  180 – 104 +40 =76

In trapezoid, Angles next to each other sum up to 180°
m∠PSR = 180 -104 = 76°
m∠QSR = 76 -40= 36°
m∠QRS= 104
m∠d= 180 – 36 +40= 104°

Problem Solving

Solve. Show your work.

The graph shows a measurement in yards (x-axis) and its corresponding measurement in feet (y-axis).

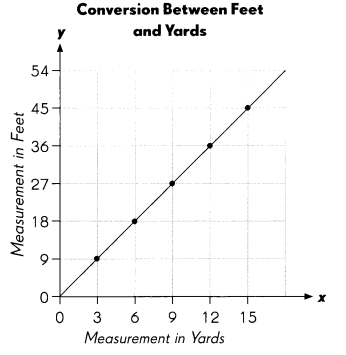
Question 55.
The cost of 3 yards of fabric is $24. What is the cost of 36 feet of fabric?
Answer: $96
Explanation:
As per graph
3 yards and 9 feets = $24
So 36 feets= 12 yards
So 12yards price is 4 x $24 = $96

Solve. Show your work.

Question 56.
Each letter of the word JOURNAL is written on separate cards and put into a bag. First, one card is drawn. Then, the card is colored blue or yellow.

a. Draw a tree diagram to show the possible combinations of cards and colors.
Answer:

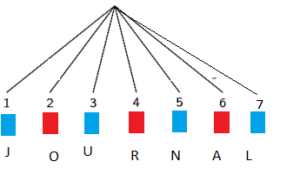
Explanation:
4 is colored blue
and 3 is colored red

b. What is the theoretical probability of picking a combination with a vowel?
Answer:
1 : 2 is the is the theoretical probability of picking a combination with a vowel

Solve. Show your work.

Question 57.
In the triangle ABC, AB = 4 centimeters, BC = 7 centimeters and AC is longer than 8 centimeters. If the length of \(\overline{A C}\) is in whole centimeters, what are the possible lengths of \(\overline{A C}\)?
Answer: AC = 9 or 10 centimeters
Explanation:
In a Triangle, sum of two sides should be greater than other side.
AC is longer than 8 centimeters. 4+ 7 is 11. so AC should not be longer than 11cm
4+7 > 9
4+9 > 7
7 + 9 > 4
or
4+7 > 10
4+10 > 7
7 + 10 > 4

Question 58.
ABCD is a trapezoid and ABED is a parallelogram. \(\overline{A B}\) || \(\overline{D C}\), \(\overline{A D}\) || \(\overline{B E}\), and BE = BC. Find the measure of ∠BCE.

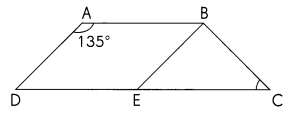
Answer:
m∠BCE = 45°
Explanation: