Math in Focus Grade 5 Chapter 6 Answer Key Area

Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 6 Area to score better marks in the exam.

Math in Focus Grade 5 Chapter 6 Answer Key Area

Math Journal

Question 1.
Four students found the area of the shaded triangle.

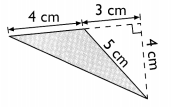
These are their findings.
Zach: 4 × 4 = 16 cm²
Preeti: \(\frac{1}{2}\) × 5 × 4 = 10 cm²
Brian: \(\frac{1}{2}\) × 7 × 4 = 14 cm²
James: \(\frac{1}{2}\) × 3 × 4 = 6 cm²

Explain the mistakes they have made. Then write the correct answer.
Zach: ________
Preeti: __________
Brian: ______
James: ________
The area of the shaded triangle is: ________
Answer:
Zach: He didn’t consider the fraction 1/2 to calculate the area of the triangle.
Preeti: Base of the triangle is not 5. Hence the answer provided is wrong.
Brain: Base of the triangle is not 7. Hence the answer provided is wrong.
James: Base of the triangle is not 3. Hence the answer provided is wrong.
Area of the shaded triangle = 1/2 × b × h
= 1/2 × 4 × 4
= 8 cm²

Question 2.

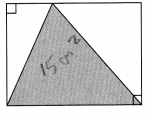
The area of the shaded triangle is 15 square centimeters. Explain why the area of the rectangle is 30 square centimeters.
Answer:
Area of the triangle = 1/2 × base × height
Area of the rectangle = base × height
= 2 × (1/2 × b × h)
= 2 × Area of triangle
= 2 × 15 cm²
= 30 cm²

Question 3.
ABCD is a rectangle and BE = EC.

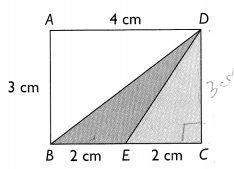
What can you say about the areas of triangles BED and ECD? Explain your answer.
Answer:
Base and height are same for both the triangles. So, area (1/2 × b × h) of the both triangles will be same.

Put on Your Thinking Cap!

Challenging Practice

Solve. Show your work.

Question 1.
ABCD is a square of side 10 centimeters and BE = EC. Find the area of the shaded triangle.

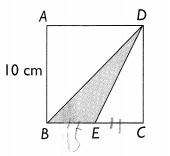
Answer:

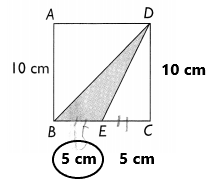
Explanation:
In the above image we can observe ABCD is a square of side 10 centimeters and BE = EC.
Area = 1/2 x b x h
1/2 x 5 x 10
25 square centimeters
Area of the shaded triangle is 25 square centimeters.

Question 2.
ABCD is a rectangle 18 centimeters by 8 centimeters. AE = ED and AF = FB. Find the area of the shaded triangle.

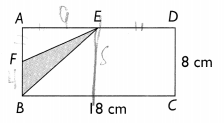
Answer:

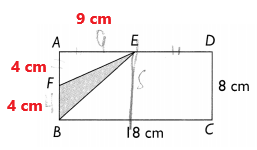
Explanation:
In the above image we can observe ABCD is a rectangle 18 centimeters by 8 centimeters.  Here AE = ED and
AF = FB.
Area = 1/2 x b x h
1/2 x 4 x 9
18 square centimeters
The area of the shaded triangle is 18 square centimeters.

Question 3.
ABCD is a rectangle of area 48 square inches. The length of CD is 3 times the length of DF. BC = 4 inches.

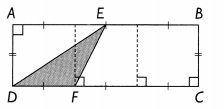
a. Find the length of DF.
Answer:

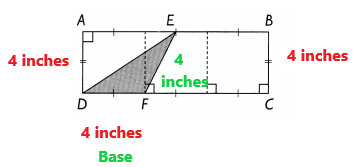
Explanation:
ABCD is a rectangle of area 48 square inches. The length of CD is 3 times the length of DF. Here BC = 4 inches.
The length of DF is 4 inches.

b. Find the area of the shaded triangle.
Answer:

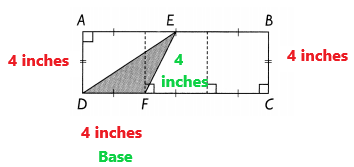
Explanation:
In the above image, we can observe ABCD is a rectangle of area 48 square inches. The length of CD is 3 times the length of DF. Here BC = 4 inches.
Area = 1/2 x b x h
1/2 x 4 x 4
8 square inches
Area of the shaded triangle is 8 square inches.

Question 4.
ABCD is a rectangle 12 centimeters by 5 centimeters. BE = 4 centimeters. Find the area of the shaded region, ABED.

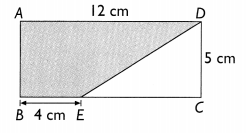
Answer:

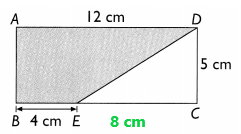
Explanation:
In the above image, we can observe  ABCD is a rectangle 12 centimeters by 5 centimeters. Here BE = 4 centimeters.
Area of unshaded region = 1/2 x b x h
1/2 x 8 x 5
20 square centimeters
Area of shaded region = 12 x 5 – 20
60 – 20
40 square centimeters
The area of the shaded region is 40 square centimeters.

Question 5.
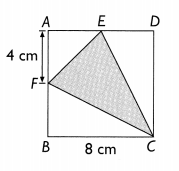
The side of square ABCD is 8 centimeters. AE = AF = 4 centimeters. Find the area of the shaded triangle, CEF.

Answer:

Explanation:
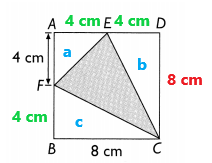
In the above image we can observe the side of square ABCD is 8 centimeters. Here AE = AF = 4 centimeters.
Area of a square = 8 x 8 = 64 square centimeters
Area of a triangle a = 1/2 x b x h
a = 1/2 x 4 x 4
a = 8 square centimeters
Area of triangle b = 1/2 x b x h
b = 1/2 x 8 x 4
b = 16 square centimeters
Area of triangle c = 1/2 x b x h
c = 1/2 x 8 x 4
c = 16 square centimeters
Area of shaded triangle = 64 – 8 – 16 – 16
Area of shaded triangle =24 square centimeters

Question 6.
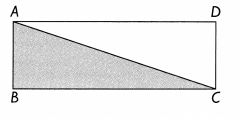
The perimeter of rectangle ABCD is 256 inches. Its length is 3 times as long as its width. Find the area of triangle ABC.

Answer:

Explanation:
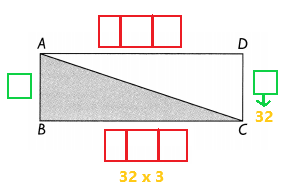
In the above image we can observe the perimeter of the rectangle ABCD is 256 inches. Its length is 3 times as long as its width.
We know that 8 units = 256 inches
4 units = 128 inches
2 units = 64 inches
1 unit = 32 inches
Here width = 32 inches
Length = 32 x 3 = 96 inches
Area of the triangle ABC = 32 x 96 = 3,072 inches

Question 7.
ABCD is a rectangle of area 72 square centimeters. The length of AD is 3 times the length of AE. BF = 8 centimeters.

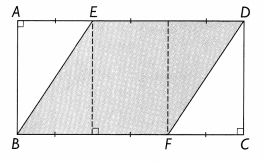
a. Find the width of the rectangle.
Answer:

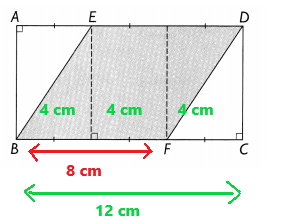
Explanation:
In the above image we can observe ABCD is a rectangle of area 72 square centimeters.
The length of AD is 3 times the length of AE. Here BF = 8 centimeters.
Width of the rectangle = 72/12 = 7 cm

b. Find the area of the shaded region, EBFD.
Answer:

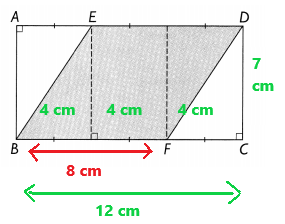
Explanation:
We know that width is equal to 7cm.
Area of the shaded region EBFD = 8 x 7 = 56 square centimeters

Put On Your Thinking Cap!

Problem Solving

Question 1.
Look at the pattern of these triangles.

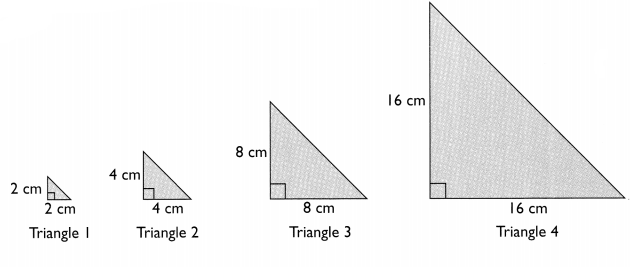
What is the area of Triangle 5 in the pattern? _____
Which triangle in the pattern will have an area of 32,768 square centimeters? _____
Answer:
The Triangle 5 has the base as 32 cm and height as 32 cm.
The area of the Triangle 5 = 1/2 x base x height
1/2 x 32 x 32
512 square centimeters
The area of the Triangle 5 is 512 square centimeters.

The Triangle 6 has the base as 64 cm and height as 64 cm.
The area of the Triangle 6 = 1/2 x base x height
1/2 x 64 x 64
2,048 square centimeters
The area of the Triangle 6 is 2,048 square centimeters.

The Triangle 7 has the base as 128 cm and height as 128 cm.
The area of the Triangle 7 = 1/2 x base x height
1/2 x 128 x 128
8,192 square centimeters
The area of the Triangle 7 is 8,192 square centimeters.
The Triangle 8 has a base as 256 cm and a height of 256 cm.
The area of the Triangle 8 = 1/2 x base x height
1/2 x 256 x 256
32,768 square centimeters
The area of the Triangle 8 is 32,768 square centimeters.
The triangle 8 in the pattern will have an area of 32,768 square centimeters.

Question 2.
ABCD is a square with sides of 20 centimeters. AX = XB, BY = YC, CZ = ZD, AW = WD. WY and XZ are straight lines. Find the total area of the shaded parts.

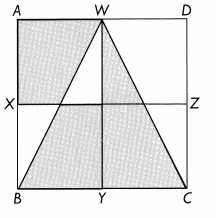
Answer:

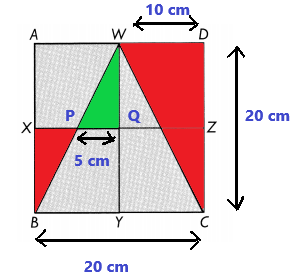
Explanation:
In the above image, we can observe ABCD is a square with sides of 20 centimeters.
Here AX = XB, BY = YC, CZ = ZD, AW = WD. WY and XZ are straight lines.
The area of triangle WDC = 1/2 x 10 x 20 = 100 square centimeters
The area of triangle WPQ = 1/2 x 5 x 10 = 25 square centimeters
The area of triangle XPB = 25 square centimeters
Area of the shaded region = Area of the whole square – Area of WDC – Area of WPQ – Area of XPB
20 x 20 – 100 – 25 – 25
400 – 100 – 25 – 25
250 square centimeters
Area of the shaded region = 250 square centimeters.

Must Read:

PEL Pivot Point Calculator