Math in Focus Grade 3 Chapter 19 Practice 2 Answer Key Square Units (cm² and in²)

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 19 Practice 2 Square Units (cm2 and in2) detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 19 Practice 2 Answer Key Square Units (cm² and in²)

Find the area of each shaded figure in square centimeters. Then complete the table.

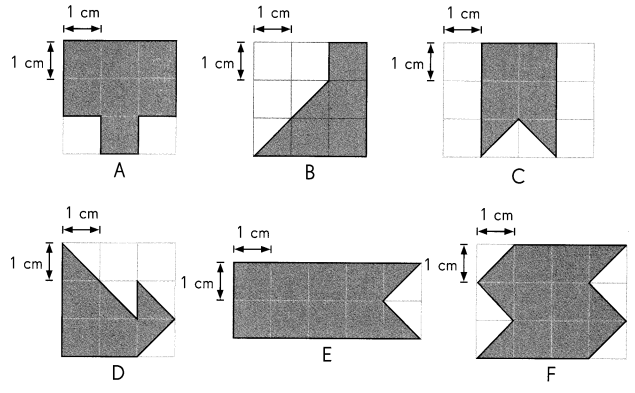
$Math in Focus Grade 3 Chapter 19 Practice 2 Answer Key Square Units (cm2 and in2) 1$

Question 1.
$Math in Focus Grade 3 Chapter 19 Practice 2 Answer Key Square Units (cm2 and in2) 2$
Answer:

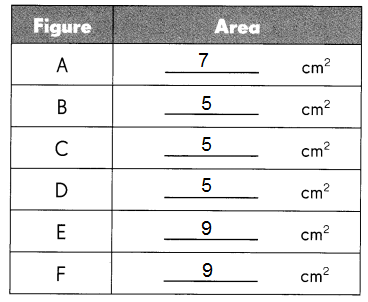
Explanation:
The simplest and most commonly used area calculations are for squares and rectangles.
To find the area of a rectangle, multiply its height by its width.
For a square you only need to find the length of one of the sides as each side is the same length and,
then multiply this by itself to find the area.

Draw two different figures with the same area on the grids.

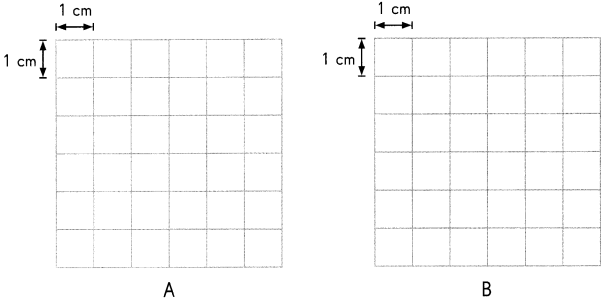
$Math in Focus Grade 3 Chapter 19 Practice 2 Answer Key Square Units (cm2 and in2) 3$
Answer:

Explanation:
In general, the area is defined as the region occupied inside the boundary of a flat object or 2d figure.
The measurement is done in square units with the standard unit being square meters (m 2).
As, it is mentioned each square 1 unit square and each half square is half square unit.
So, by calculating each 1 square unit and half square units in the figure, we find Area.
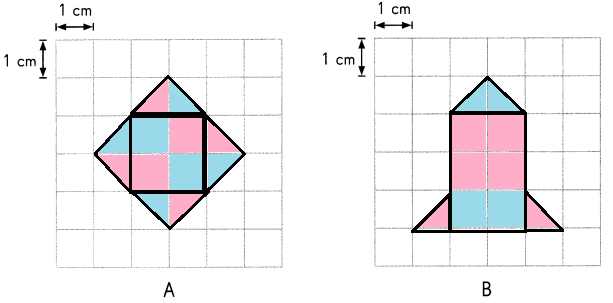
The area of each figure A is 8 cm².
The area of each figure B is 8 cm².

Question 2.
What is the area of the figures?
Answer: 8 cm²
Explanation:
Drawings may differ from one to one.
In the above grid each square is equal to 1 unit.
The area of drawn pictures in the grid is 8 square units.
In figure A it has 4 full squares and 8 half squares.
In figure B it has 6 full squares and 4 half squares.
So, the area of both figures = 8 cm².

Question 3.
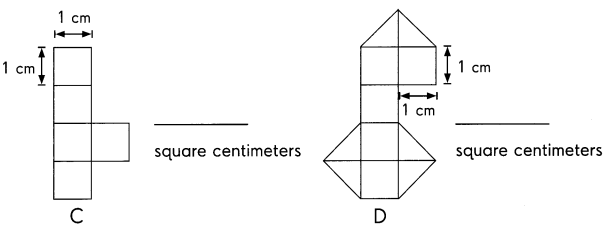
The figures are made of square and half-square tiles. Find the area of each figure.
$Math in Focus Grade 3 Chapter 19 Practice 2 Answer Key Square Units (cm2 and in2) 4$
Answer:

Explanation:
The simplest and most commonly used area calculations are for squares and rectangles.
To find the area of a figures is by adding all the areas covered by the squares and triangles,
two triangles is one square.

Question 4.
Which figure has a larger area? Figure _____________
Answer:
Figure D has largest area
Explanation:
The simplest area calculations are for squares and rectangles.
To find the area of a figures is by adding all the areas covered by the squares and triangles,
two triangles is one square.
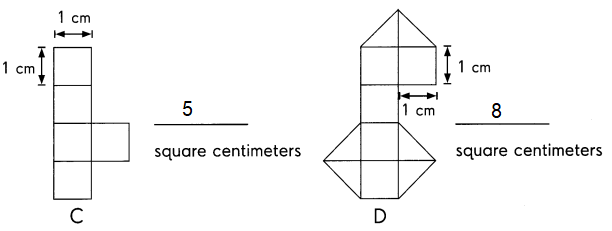
Figure D has largest area of 8 cm²

Question 5.
How can you make both figures have the same area?
Answer:
By adding 3 square centimeters to the figure C ,
we can make both the figures as same area.
Explanation:
Observe the given figure C and D ,
Figure C has 3 units less than figure D.

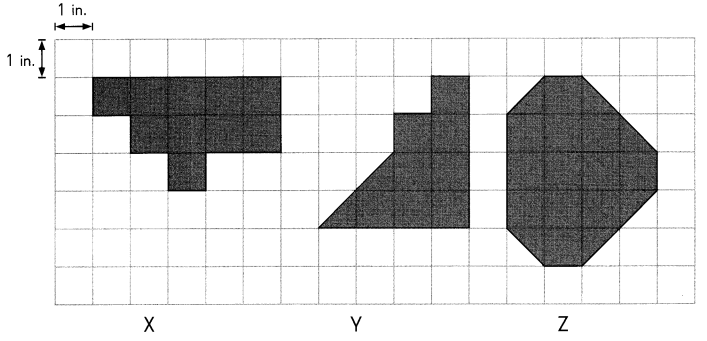
Find the area of each shaded figure in square inches. Then complete the table.

$Math in Focus Grade 3 Chapter 19 Practice 2 Answer Key Square Units (cm2 and in2) 5$

Question 6.
$Math in Focus Grade 3 Chapter 19 Practice 2 Answer Key Square Units (cm2 and in2) 6$
Answer:

Explanation:
The simplest and most commonly used area calculations are for squares and rectangles.
To find the area of a figures is by adding all the areas covered by the squares and triangles,
two triangles is one square.

Draw two different figures with the same area on the grid.

Question 7.
$Math in Focus Grade 3 Chapter 19 Practice 2 Answer Key Square Units (cm2 and in2) 7$
Answer:

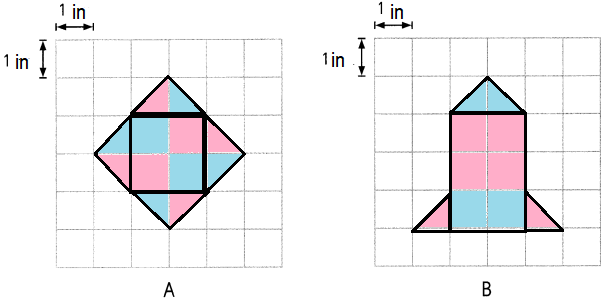
Explanation:
The simplest and most commonly used area calculations are for squares and rectangles.
To find the area of a figures is by adding all the areas covered by the squares and triangles,
two triangles is one square.
The area of each figure A is 8 in².
The area of each figure B is 8 in².

Question 8.
The area of each figure is ____________ in.².
Answer: 8 in.²Explanation:
The simplest and most commonly used area calculations are for squares and rectangles.
To find the area of a figures is by adding all the areas covered by the squares and triangles, two triangles is one square
The area of each figure A is 8 in.².
The area of each figure B is 8 in.².

Find the area of each shaded figure in square inches. Then complete the table.

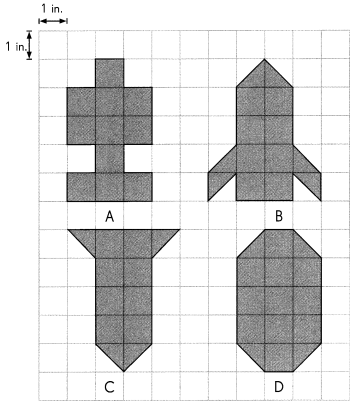
$Math in Focus Grade 3 Chapter 19 Practice 2 Answer Key Square Units (cm2 and in2) 8$

Question 9.
$Math in Focus Grade 3 Chapter 19 Practice 2 Answer Key Square Units (cm2 and in2) 9$
Answer:

Explanation:
The simplest and most commonly used area calculations are for squares and rectangles.
To find the area of a figures is by adding all the areas covered by the squares and triangles,
two triangles is one square.

Question 10.
Figure __________ and Figure __________ have the same area.
Answer:
Figure A and Figure B have the same area of 11in.²Explanation:
Compare the figures A and B,
the area of both the figures is same as 11in.²Question 11.
Figure ___________ has the largest area.
Answer:
Figure D has the largest area of 13 in.²Explanation:
Compare all the given figures,
Area of figure D is the greatest with 13 in.²Question 12.
Figure __________ has the smallest area.
Answer: C
Figure C has the smallest area of 10 in.²Explanation:
Compare all the given figures,
Area of figure C is the least with 10 in.²

$Math in Focus Grade 3 Chapter 19 Practice 2 Answer Key Square Units (cm2 and in2) 10$

IRCTC Pivot Point Calculator

Math in Focus Grade 3 Chapter 19 Practice 2 Answer Key Square Units (cm2 and in2)