This handy Math in Focus Grade 3 Workbook Answer Key Chapter 19 Area and Perimeter provides detailed solutions for the textbook questions.
Math in Focus Grade 3 Chapter 19 Answer Key Area and Perimeter
Math Journal
Look at John’s answers for the perimeter of the squares and rectangles.
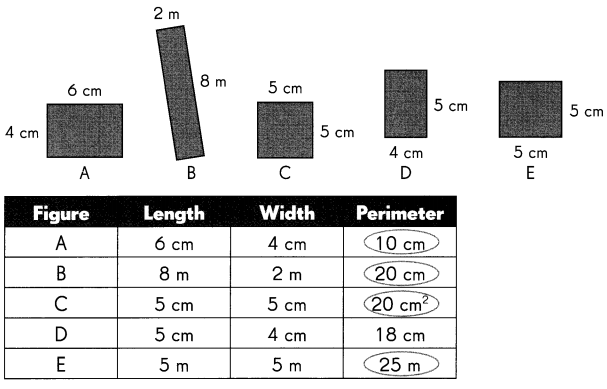
John’s mistakes are circled. Explain why his answers are not correct.
Answer:
John added only two sides to find perimeter,
the perimeter formulas for rectangles and square.
The perimeter of a rectangle is the total distance of its outer boundary.
It is twice the sum of its length and width and it is calculated with the help of the formula:
Perimeter = 2(length + width).
Explanation:
The perimeter of a square is defined as the total length that its boundary covers
The formula to calculate the perimeter of a square is as, mathematically expressed as;
Perimeter of square, (P) = 4 × Side
Write the correct answers.
Example The unit for the perimeter of Figure B should be meter (m).
Question 1.
Perimeter of Figure A: _____________________
Answer: 20 cm
Explanation:
The perimeter of a rectangle is the total distance of its outer boundary.
It is twice the sum of its length and width and it is calculated with the help of the formula.
Perimeter = 2(length + width).
P=2(6 + 4) = 2 x 10 = 20cm
Question 2.
Perimeter of Figure C: _____________________
Answer: 20 cm
Explanation:
The perimeter of a square is defined as the total length that its boundary covers
The formula to calculate the perimeter of a square is as, mathematically expressed as;
Perimeter of square, (P) = 4 × Side
P = 4 x s
= 4 x 5 = 20 cm
Question 3.
Perimeter of Figure E: _____________________
Answer: 20cm
Explanation:
The perimeter of a square is defined as the total length that its boundary covers.
The formula to calculate the perimeter of a square is as, mathematically expressed as;
Perimeter of square, (P) = 4 × Side
Put On Your Thinking Cap!
Challenging Practice
Complete.
Question 1.
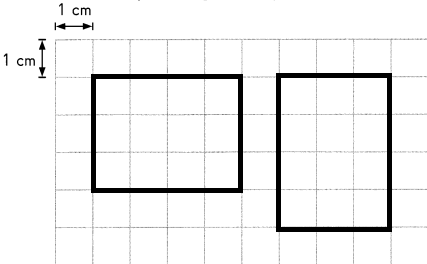
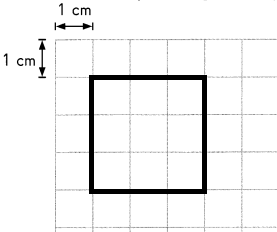
Draw different rectangles with an area of 12 square centimeters. Then draw different rectangles with an area of 9 square centimeters. How many rectangles can you draw for each area?
Answer:
2 rectangles can be drawn for area of area 12 square centimeters and,
1 rectangle can be drawn for area of 9 square centimeters.
Explanation:
The area of rectangle (A) is the product of its length ‘a’ and width or breadth ‘b’.
So, Area of Rectangle = (a × b) square units.
The square is a shape with four equal sides.
The area of a square is defined as the number of square units that make a complete square.
It is calculated by using the formula Area = s × s = s2 in square units.
So, area = 9 square centimeters.
Solve.
Question 2.
Karl bends a piece of wire into a square as shown.

Answer: 32cm
Explanation:
The perimeter of a square is defined as the total length that its boundary covers,
The formula to calculate the perimeter of a square is as, mathematically expressed as;
Perimeter of square, (P) = 4 × Side
P = 4 x 8 = 32 cm
Which of these rectangles can he make using the same piece of wire?
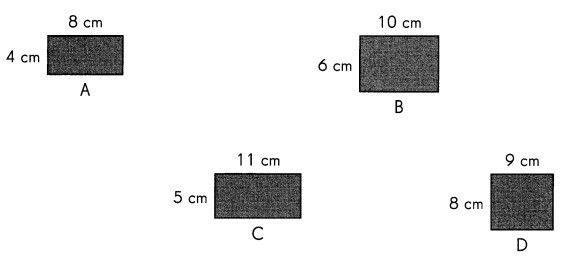
Answer:
Rectangle B and C perimeter is 32cm.
Explanation:
Perimeter of rectangle A
Perimeter = 2(length + width).
P=2(8 + 4) = 2 x 12 = 24cm
Perimeter of rectangle B
Perimeter = 2(length + width).
P=2(10 + 6) = 2 x 16 = 32cm
Perimeter of rectangle C
Perimeter = 2(length + width).
P=2(11 + 5) = 2 x 16 = 32cm
Perimeter of rectangle D
Perimeter = 2(length + width).
P=2(9 + 8) = 2 x 17 = 34cm
Question 3.
Ally wants to build an exercise pen for her pet rabbit. She has 36 feet of fencing to build a rectangular enclosure in her yard. She wants to carefully plan the length and width of the pen, measuring in units of whole feet.
Find all the possible ways that Ally could build her pen and have a perimeter of 36 feet. Fill in the table below.
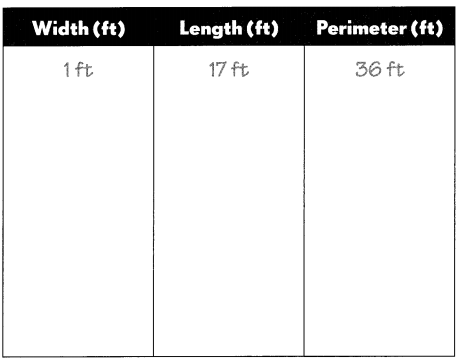
Answer:
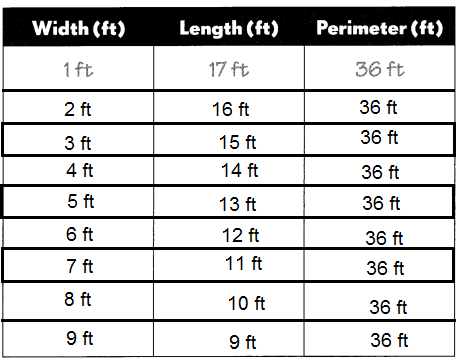
Explanation:
Ally wants to build an exercise pen for her pet rabbit.
So, Perimeter = 2(length + width)
Perimeter = 2(1 + 17) = 36 ft
Perimeter = 2(2 + 16) = 36 ft
Perimeter = 2(3 + 15) = 36 ft
Perimeter = 2(4 + 14) = 36 ft
Perimeter = 2(5 + 13) = 36 ft
Perimeter = 2(6 + 12) = 36 ft
Perimeter = 2(7 + 11) = 36 ft
Perimeter = 2(8 + 10) = 36 ft
Perimeter = 2(9 + 9) = 36 ft
Question 4.
What are some of the concerns that Ally needs to think of in planning for the exercise pen?
Answer:
Perimeter and area of exercise pen.
length and width of exercise pen.
Explanation:
The above are some of the concerns that Ally needs to think of in planning for the exercise pen.
Put On Your Thinking Cap!
Problem Solving
Solve. Look at this pattern.
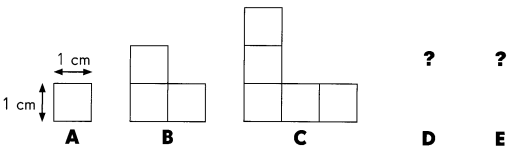
What is the area of each figure?
Answer:
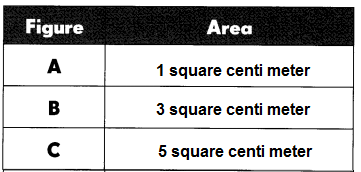
Explanation:
In the above picture each area of the square is measured as 1 square centimeter.
In figure A there is only 1 square box.
In figure B there are 3 square boxes.
In figure C there are 5 square boxes.
If the pattern continues, what will the area of Figure E be? Draw Figure E below.
Answer:
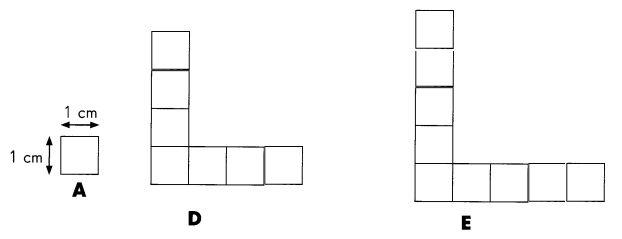
the area of Figure D & E

Explanation:
In the above picture each area of the square is measured as 1 square centimeter.
In figure D there are 7 square units.
In figure E there are 9 square units.
Must Read: