This handy Math in Focus Grade 6 Workbook Answer Key Chapter 11 Lesson 11.2 Area of a Circle detailed solutions for the textbook questions.
Math in Focus Grade 6 Course 1 B Chapter 11 Lesson 11.2 Answer Key Area of a Circle
Math in Focus Grade 6 Chapter 11 Lesson 11.2 Guided Practice Answer Key
Complete. Use 3.14 as an approximation for π.
Question 1.
Find the area of a circle that has a radius of 18 centimeters.
Area = πr2
≈ ![]() •
• ![]()
= ![]() •
• ![]()
= ![]() cm2
cm2
The area of the circle is approximately ![]() square centimeters
square centimeters
Answer:
The area of the circle is approximately 1,017 square centimeters,
Explanation:
Given radius as 18 centimeters as the area of the circle is πr2, So area = 3.14 X 18 cms X 18 cms = 1,017.36 cm2 approximately 1,017 square centimeters.
Question 2.
Find the area of a circle that has a radius of 15 inches.
Area = πr2
≈ ![]() •
• ![]()
= ![]() •
• ![]()
= ![]() in.2
in.2
The area of the circle is approximately ![]() square inches.
square inches.
Answer:
The area of the circle is approximately 707 square inches,
Explanation:
Given radius as 15 inches as the area of the circle is πr2, So area = 3.14 X 15 in X 15 in = 706.5 in2 approximately 707 square inches.
Question 3.
Find the area of a circle that has a diameter of 26 centimeters.
Radius = diameter ÷ 2
= ![]() ÷
÷ ![]()
= ![]() cm
cm
Area = πr2
≈ ![]() •
• ![]() •
• ![]()
= ![]() •
• ![]()
= ![]() cm2
cm2
The area of the circle is approximately ![]() square centimeters.
square centimeters.
Answer:
The area of the circle is approximately 531 square centimeters,
Explanation:
Given diameter as 26 cms so radius = diameter ÷ 2 = 26 cms ÷ 2 = 13 cms as the area of the circle is πr2, So area = 3.14 X 13 cms X 13 cms = 530.66 cm2 approximately 531 square centimeters.
Complete. Use \(\frac{22}{7}\) as an approximation for π.
Question 4.
Find the area of a quadrant.
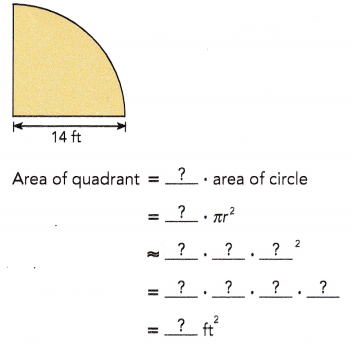
The area of a quadrant is approximately ![]() square feet.
square feet.
Answer:
The area of the quadrant is approximately 154 square feet,
Explanation:
Given radius is 14 ft as area of quardant is \(\frac{1}{4}\) X area of circle = \(\frac{1}{4}\) X πr2 = \(\frac{1}{4}\) X 3.14 X 14 feet X 14 feet = 153.86 square feet approximately 154 square feet.
Question 5.
The diameter of a circle is 42 inches. Find the area of a quadrant.
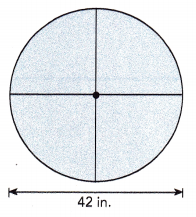
Radius = diameter ÷ 2
= ![]() ÷ 2
÷ 2
= ![]() in.
in.
Area of quadrant = ![]() • area of circle
• area of circle
= ![]() • πr2
• πr2
≈ ![]() •
• ![]() •
• ![]()
= ![]() •
• ![]() •
• ![]() •
• ![]()
= ![]() in.2
in.2
The area of a quadrant is approximately ![]() square inches.
square inches.
Answer:
The area of the quadrant is approximately 346 square inches,
Explanation:
Given diameter as 42 inches so radius = 42 inches/2 = 21 inches as area of quardant is \(\frac{1}{4}\) X area of circle = \(\frac{1}{4}\) X πr2 = \(\frac{1}{4}\) X 3.14 X 21 inches X 21 inches = 346.185 square inches approximately 346 square inches.
Math in Focus Course 1B Practice 11.2 Answer Key
Find the area of each circle. Use 3.14 as an approximation for π.
Question 1.
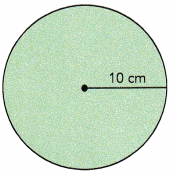
Answer:
The area of the circle is 314 square centimeters,
Explanation:
Explanation:
Given radius as 10 cm as the area of the circle is πr2, So area = 3.14 X 10 cm X 10 cm = 314 cm2 .
Question 2.
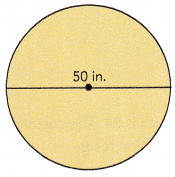
Answer:
The area of the circle is approximately 1,963 square inches,
Explanation:
Given diameter as 50 inches so radius = diameter ÷ 2 = 50 in ÷ 2 = 25 in as the area of the circle is πr2, So area = 3.14 X 25 in X 25 in =1962.5 inches2 approximately 1,963 square inches.
Find the area of each semicircle. Use \(\frac{22}{7}\) as an approximation for π.
Question 3.
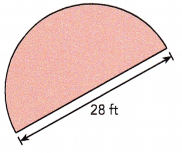
Answer:
The area of semicircle is 307.72 square feet,
Explanation:
Given diameter as 28 ft so radius = diameter ÷ 2 = 28 ft ÷ 2 = 14 ft as the area of the circle is πr2, So area = 3.14 X 14 ft X 14 ft = 615.44 square feet, The area of semicircle is half the area of the circle so it is \(\frac{1}{2}\) X
615.44 square feet = 307.72 square feet.
Question 4.
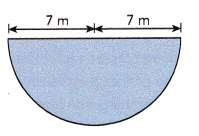
Answer:
The area of semicircle is 76.93 square meter,
Explanation:
Given radius as 7 m the area of the circle is πr2, So area = 3.14 X 7 m X 7 m = 153.86 square meter, The area of semicircle is half the area of the circle so it is \(\frac{1}{2}\) X
153.86 square meter = 76.93 square meter.
Find the area of each quadrant to the nearest tenth. Use 3.14 as an approximation for π.
Question 5.
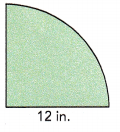
Answer:
The area of quardant is 113.04 square inches,
Explanation:
Given radius as 12 inches the area of the circle is πr2, So area = 3.14 X 12 in. X 12 in. = 452.16 square inches, The area of quardant is 1/4 of the area of the circle so it is \(\frac{1}{4}\) X 452.16 square inches = 113.04 square inches.
Question 6.
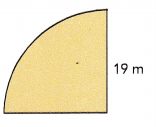
Answer:
The area of quardant is 283.385 square meters,
Explanation:
Given radius as 19 meters the area of the circle is πr2, So area = 3.14 X 19 m X 19 m = 1,133.54 square meters, The area of quardant is 1/4 of the area of the circle so it is \(\frac{1}{4}\) X 1,133.54 square meters = 283.385 square meters.
Solve. Show your work.
Question 7.
A circular pendant has a diameter of 7 centimeters. Find its area. Use \(\frac{22}{7}\) as an approximation for π.
Answer:
Area = 38.465 square centimeters,
Explanation:
Given a circular pendant has a diameter of 7 centimeters. So radius = diameter ÷ 2 = 7 cms ÷ 2 = 3.5 cms, As area of circle = πr2, So area = 3.14 X 3.5 cms X 3.5 cms = 38.465 square centimeters.
Question 8.
The shape of the stage of a lecture theater is a semicircle. Find the area of the stage. Use 3.14 as an approximation for π.
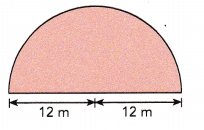
Answer:
The area of the stage is 226.08 square meter,
Explanation:
Given shape of the stage of a lecture theater is a semicircle with radius 12 m, First area of circle is πr2, So area = 3.14 X 12 m X 12 m = 452.16 square meter, Now area of semicircle is \(\frac{1}{2}\) X 452.16 sq mt = 226.08 square meter.
Question 9.
The shape of a balcony floor is a quadrant. Find the area of the balcony floor. Use 3.14 as an approximation for π.
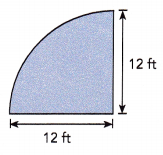
Answer:
The area of the balcony floor is 113.04 square feet,
Explanation:
Given shape of a balcony floor is a quadrant with radius 12 ft, First area of circle is πr2, So area = 3.14 X 12 ft X 12 ft = 452.16 square feet, Now area of quadrant is \(\frac{1}{4}\) X 452.16 square feet = 113.04 square feet.
Question 10.
The cost of an 8-inch pizza is $4. The cost of a 16-inch pizza is $13. Use 3.14 as an approximation for π.
a) How much greater is the area of the 16-inch pizza than the area of the 8-inch pizza?
Answer:
Greater is the area of the 16-inch pizza than the area of the 8-inch pizza is 150.72 square inches,
Explanation:
Area of 8 inch pizza radius is 8 inch ÷ 2 = 4 inch, Area of 8 inch pizza = 3.14 X 4 inch X 4 inch = 50.24 square inch,
Area of 16 inch pizza is 16 inch ÷ 2 = 8 inch, Area of 16 inch pizza = 3.14 X 8 inch X 8 inch = 200.96 square inch,
Now the area of the 16-inch pizza than the area of the 8-inch pizza is 200.96 square inch – 50.24 square inch = 150.72 square inches.
b) Which is a better deal? Explain your reasoning.
Answer:
8 inch pizza,
Explanation:
Cost of 16 inch pizza is $13, So cost of 1 inch pizza is $13/16 = $0.8125,
Cost of 8 inch pizza is $4, So cost of 1 inch pizza is $4/8 = $0.5 therefore it is better to buy 8 inch pizza as in 1 inch it cost $0.5 than 16 inch pizza in which 1 inch is $0.8125.
Question 11.
Four identical drinking glasses each have a radius of 5 centimeters. The glasses are arranged so that they touch each other as shown in the figure below. Find the area of the green portion. Use 3.14 as an approximation for π.
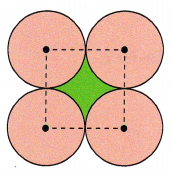
Answer:
The area of the green portion is 21.5 square centimeters,
Explanation:
Given to find the area of green portion so it is the area of square minus area of 4 quadrants so ((the area of square – 4(\(\frac{1}{4}\) X πr2)) = 10 cms x 10 cms – 4(\(\frac{1}{4}\) X 3.14 X 5 cms X 5 cms) = 100 square cms – 3.14 X 25 square cms = 100 square cms – 78.5 square cms = 21.5 square centimeters.
Question 12.
The figure is made up of trapezoid ABCD and a semicircle. The height of trapezoid ABCD is \(\frac{5}{6}\) the length of \(\overline{B C}\). Find the area of the figure. Use \(\frac{22}{7}\) as an approximation for π.
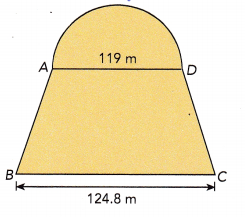
Answer:
Total area of trapezoid ABCD and a semicircle is 18,235.7925 square meters,
Explanation:
The area of trapezoid is 1/2 X (base1 + base2) X height, where base1 and base2 are lengths of parallel sides, we have height as \(\frac{5}{6}\) X 124.8 m = 104 m, Now area of trapezoid is 1/2 X (124.8 m + 119 m) X 104 m = 1/2 X 243.8 m X 104 m =12,677.6 square meters. First we calculate area of circle as diameter is 119 m so radius = 119 m/2 = 59.5 m, Area = 3.14 X 59.5 m x 59.5 m = 11,116.385 square meter, Now area of semicircle is half the area of circle = 11,116.385 square mt/2 = 5,558.1925 square meter, So total area of trapezoid ABCD and a semicircle is
area trapezoid + area of semicircle = 12,677.6 square meters + 5,558.1925 square meters = 18,235.7925 square meters.