Math in Focus Grade 6 Chapter 11 Lesson 11.1 Answer Key Radius, Diameter, and Circumference of a Circle

Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 11 Lesson 11.1 Radius, Diameter, and Circumference of a Circle to score better marks in the exam.

Math in Focus Grade 6 Course 1 B Chapter 11 Lesson 11.1 Answer Key Radius, Diameter, and Circumference of a Circle

Math in Focus Grade 6 Chapter 11 Lesson 11.1 Guided Practice Answer Key

Question 1.
In the figure, 0 ¡s the center of the circle with \(\overline{A B}\), \(\overline{C D}\), and \(\overline{E D}\) as shown.

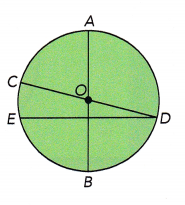
a) Name all the diameters that are drawn in the circle.
Answer:
AB, CD,

Explanation:
A diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle, all the diameters that are drawn in the circle are AB, CD.

b) Which line segment that joins two points on the circle ¡s not a diameter? Explain why it ¡s not a diameter.
Answer:
DE,

Explanation:
A line segment that crosses the circle by passing through its center is called a diameter. As DE doesnot cross through the circle.

Question 2.
The radius of a circle is 6 centimeters. What is the length of its diameter?
Diameter = 2 • radius
=
= cm
The diameter of the circle is centimeters.
Answer:
12 centimeters,

Explanation:
Given the radius of a circle is 6 centimeters, So the length of its diameter as diameter = 2 X radius,
Diameter = 2 X 6 centimeters = 12 centimeters.

Question 3.
The diameter of a circle is 15 inches. What is the length of its radius?
Radius = diameter ÷ 2
= ²
= in.
The radius of the circle is inches.
Answer:
7.5 inches,

Explanation:
Given the diameter of a circle is 15 inches, So the length of it radius is as radius = diameter ÷ 2 = 15 inches ÷ 2 = 7.5 inches.

Hands-On Activity

Materials

• compass

DRAWING CIRCLES USING A COMPASS

Step 1: Measure 5 centimeters on a ruler with a compass.
Example

Step 2: Then draw a circle. Draw and label the center O and four radii: \(\overline{O P}\), \(\overline{O Q}\), \(\overline{O R}\) and \(\overline{O S}\).
Example

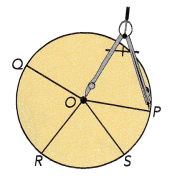
Step 3: Measure the radii \(\overline{O P}\), \(\overline{O Q}\), \(\overline{O R}\), and \(\overline{O S}\). What can you say about the lengths of \(\overline{O P}\), \(\overline{O Q}\), \(\overline{O R}\), and \(\overline{O S}\)?
Answer:
\(\overline{O P}\) = 5 centimeters, \(\overline{O Q}\) = 5 centimeters, \(\overline{O R}\), = 5 centimeters and \(\overline{O S}\) = 5 centimeters,

Explanation:
The lengths of \(\overline{O P}\), \(\overline{O Q}\), \(\overline{O R}\), and \(\overline{O S}\) are 5 centimeters as we measured 5 centimeters on a ruler with a compass and then drawa a circle and labelled the center O and four radii \(\overline{O P}\), \(\overline{O Q}\), \(\overline{O R}\) and \(\overline{O S}\) so the lengtha are 5 cm each.

Hands-On Activity

INVESTIGATING THE RELATIONSHIP BETWEEN THE CIRCUMFERENCE AND DIAMETER OF A CIRCLE

Step 1: Lisa uses a string to measure the circumference of each circle to the nearest tenth of a centimeter and records it in a table.

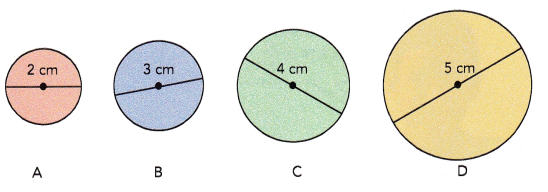
Copy the table. Divide the circumference of each circle by its diameter. Round your answers to the nearest tenth. Record your results.

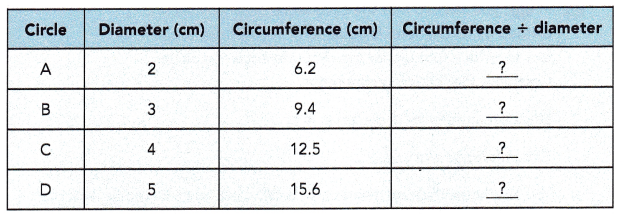
What do you notice about the quotients in the last column?
The circumference of any circle divided by its diameter always gives the same value.

The Greek letter π is used to represent this value.

Step 2: To see the value of π up to 9 decimal places, press π Enter on your calculator. Round the value of π to
a) the nearest tenth.
b) the nearest hundredth.
c) the nearest thousandth.

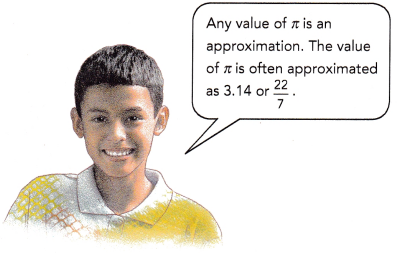
Step 3: In Step 1, you learned that the circumference of any circle divided by its diameter is equal to n. You can use this fact to write a formula for the circumference of a circle.
Complete the following statement.
Since circumference ÷ diameter = π,
Circumference = π •
You also know that the diameter of a circle is 2 times its radius. You can use this fact to write a related formula for the circumference of a circle. Complete the following statement.
Circumference = π • diameter
= π • 2 •
= 2 • π •
Using C for circumference, d for diameter, and r for radius, you can write these formulas as
C = πd
C = 2πr
Math Note
πd means π • d and 2πr means 2 • π • r.
Answer:

Explanation:
The quotients in the last column is the circumference of any circle divided by its diameter always gives the same value 3.14.

Copy and complete the table. Use \(\frac{22}{7}\) as an approximation for π.

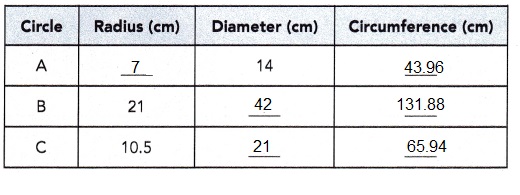
Question 4.

Answer:

Explanation:
Given A has diameterr 14 cm so as circumfrence = πd so diameter is circumfrence/ π, 14 = circumfrence/ π,
so circumfrence = 14 X π = 14 X 3.14 = 43.96 cms, Now radius = circumfrence/ 2π = 43.96/ 2 X 3.14 = 43.96/6.28 = 7 cm. Circle B has radius 21 cm so diameter =  2r = 2 X 21 cm = 42 cms, circumfrence = 2πr = 2 X 3.14 X 21 cm = 131.88 cm and Circle C has radius 10.5 cm so diameter =  2r = 2 X 10.5 cm =  21 cms, circumfrence = 2πr = 2 X 3.14 X 10.5 cm = 65.94 cm. Completed the table as shown above.

Copy and complete the table. Use 3.14 as an approximation for π.

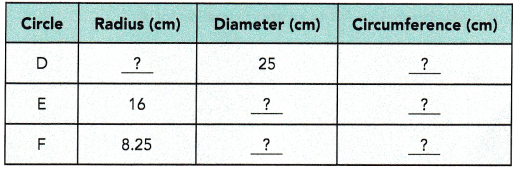
Question 5.

Answer:

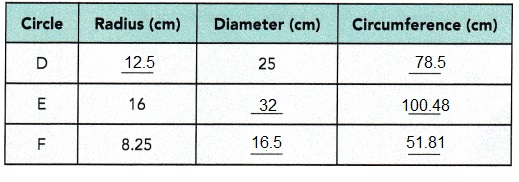
Explanation:
Given D has diameterr 25 cm so as circumfrence = πd so diameter is circumfrence/ π, 25 = circumfrence/ π,
so circumfrence = 25 X π = 25 X 3.14 = 78.5 cms, Now radius = circumfrence/ 2π = 78.5/ 2 X 3.14 =78.5/6.28 = 12.5 cm. Circle E has radius 16 cm so diameter =  2r = 2 X 16 cm = 32 cms, circumfrence = 2πr = 2 X 3.14 X 16 cm = 100.48 cm and Circle F has radius 8.25 cm so diameter =  2r = 2 X 8.25 cm = 16.5 cms, circumfrence = 2πr = 2 X 3.14 X 8.25 cm = 51.81 cm. Completed the table as shown above.

Complete.

Question 6.
A circular hoop is cut into two equal parts. Its diameter is 35 inches. Find the length of each semicircular arc. Use \(\frac{22}{7}\) as an approximation for π.
Circumference of hoop = πd
≈
= in.
Length of each semicircular arc = \(\frac{1}{2}\) • circumference of hoop
=
= in.
The length of each semicircular arc is approximately inches.
Answer:
The length of each semicircular arc is approximately 55 inches,

Explanation:
Given a circular hoop is cut into two equal parts. Its diameter is 35 inches. So the length of each semicircular arc. Using \(\frac{22}{7}\) as an approximation for π. Circumference of hoop = πd = 3.14 X 35 inches = 109.9 inches, Now Length of each semicircular arc = \(\frac{1}{2}\) • circumference of hoop = \(\frac{1}{2}\) X 109.9 inches = 54.95 approximately 55 inches.

Question 7.
A quadrant is cut from a square. The side of the square is 10 centimeters. Find the length of the arc of the quadrant. Use 3.14 as an approximation for π.

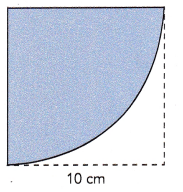
Circumference of circle = 2πr
≈ 2 • •
= cm
Length of the arc of the quadrant = circumference ÷ 4
= ÷
= cm
The length of the arc of the quadrant is approximately centimeters.
Answer:
The length of the arc of the quadrant is approximately 15.7 centimeters.,

Explanation:
Given quadrant is cut from a square. The side of the square is 10 centimeters. So the length of the arc of the quadrant by using 3.14 as an approximation for π, Circumference of circle = 2πr,  2 X 3.14 X 10 cm =62.8 cms,
Length of the arc of the quadrant = circumference ÷ 4 = 62.8 ÷ 4 = 15.7 cm, therefore the length of the arc of the quadrant is approximately 15.7 centimeters.

Hands-On Activity

DRAWING SEMICIRCLES AND QUADRANTS

Materials

• compass
• drawing triangles
• ruler
• protractor

Step 1: Use a compass to draw a circle of radius 2 inches. Label the center O.

Step 2: Draw and label a diameter of the circle \(\overline{P Q}\). What do you notice?
A diameter of a circle divides it into semicircles.
This figure is one of the semicircles.

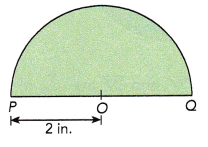
Find the distance around the semicircle. Use 3.14 as an approximation for π.

Step 3: In your circle, draw a second diameter perpendicular to \(\overline{P Q}\) using a ruler and protractor, or a drawing triangle. Label it \(\overline{R S}\). What do you notice?
a) Two perpendicular diameters of a circle divide it into quadrants.
This figure is one of the quadrants.

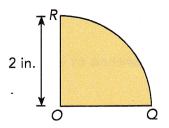
Find the distance around the quadrant. Use 3.14 as an approximation for π.
Answer:
A diameter of a circle divides it into 2 semicircles,
The distance around the quadrant is 3.14 inches,

b) This figure is made up of the semicircular arc, the arc of a quadrant, and the radii \(\overline{O R}\) and \(\overline{O Q}\). Find the distance around the figure. Use 3.14 as an approximation for π.

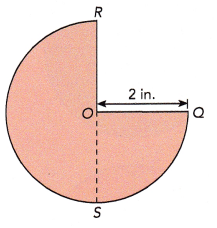
Answer:
The distance around the fiqure is 9.42 inches,

Explanation:
Step 1: Using a compass to draw a circle of radius 2 inches. Label the center O.
Step 2: Drawn and labelled a diameter of the circle \(\overline{P Q}\).
A diameter of a circle divides it into 2 semicircles.
Step 3: In my circle, drawn a second diameter perpendicular to \(\overline{P Q}\) using a ruler and protractor, or a drawing triangle. Labeledit \(\overline{R S}\).
Length of the arc of the quadrant = circumference ÷ 4, As circumfrence = 2πr,  2 X 3.14 X 2 in =12.56 inches,
= 12.56 inches/4 = 3.14 inches, The distance around the fiqure is 3 X 3.14 inches =  9.42 inches.

Math in Focus Course 1B Practice 11.1 Answer Key

Use the figure to complete. In the figure, O is the center of the circle and \(\overline{X Y}\) is a straight line.

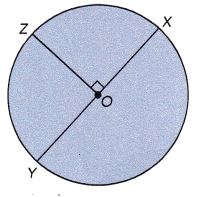
Question 1.
\(\overline{O X}\), \(\overline{O Y}\), and \(\overline{O Z}\) are of the circle.
Answer:
\(\overline{O X}\), \(\overline{O Y}\), and \(\overline{O Z}\) are radius of the circle,

Explanation:
Radius of a circle is the distance from the center of the circle to any point on it’s circumference. So \(\overline{O X}\), \(\overline{O Y}\), and \(\overline{O Z}\) are radius of the circle.

Question 2.
XY is a of the circle.
Answer:
Diameter,

Explanation:
The diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circumference of the circle. So XY ia a diameter of the circle.

Question 3.
OX = =
Answer:
OX = OY = OZ,

Explanation:
As OX is radius of the circle and the distance of OY and OZ is same so OX = OY = OZ.

Question 4.
XY = • OZ
Answer:
2 X OZ,

Explanation:
As XY id diameter so XY = 2 X OZ.

Question 5.
Circumference of the circle = π •
Answer:
Circumference of the circle = 2 X π X OX or 2 X π X OY or 2 X π X OZ,

Explanation:
As radius of circle is OX, OY, OZ so Circumference of the circle = 2 X π X OX or 2 X π X OY or 2 X π X OZ.

Find the circumference of each circle. Use \(\frac{22}{7}\) as an approximation for π.

Question 6.

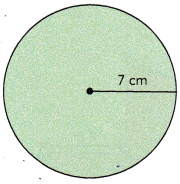
Answer:
The circumfrence is 43.96 cms,

Explanation:
As we know circumference of circle is C = 2πr given radius r = 7 cm so circumfrence = 2 X 3.14 X 7 cm = 43.96 cms.

Question 7.

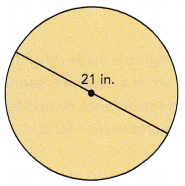
Answer:
The circumfrence is 65.94 inches,

Explanation:
As we know circumference of circle is C = πd given diameter d = 21 inches so  circumfrence = 3.14 X 21 inches = 65.94 inches.

Question 8.

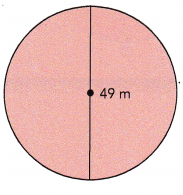
Answer:
The circumfrence is 153.86 m,

Explanation:
As we know circumference of circle is C = πd given diameter d = 49 m so circumfrence = 3.14 X 49 m = 153.86 m.

Question 9.

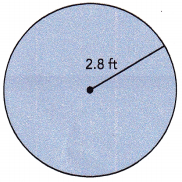
Answer:
The circumfrence is 17.584 cms,

Explanation:
As we know circumference of circle is C = 2πr given radius r = 2.8 ft so circumfrence = 2 X 3.14 X 2.8 ft = 17.584 cms.

Find the length of each arc. Use \(\frac{22}{7}\) as an approximation for π.

Question 10.

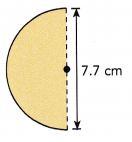
Answer:
Length of the arc = 12.089 cm,

Explanation:
Length of arc = \(\frac{1}{2}\) X circumference, Given diameter d = 7.7 cm as we know C = πd so length of
arc is \(\frac{1}{2}\) X 3.14 X 7.7 cm = 12.089 cm.

Question 11.

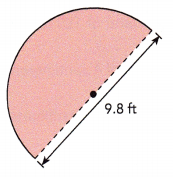
Answer:
Length of the arc = 15.386 ft,

Explanation:
Length of arc = \(\frac{1}{2}\) X circumference, Given diameter d = 9.8 ft as we know C = πd so length of
arc is \(\frac{1}{2}\) X 3.14 X 9.8 ft = 15.386 ft.

Question 12.

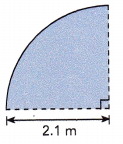
Answer:
Length of the arc = 3.297 m,

Explanation:
Length of the arc of the quadrant = circumference ÷ 4 and C = πd or 2πr as given radius = 2.1 m so circumfrence = 2 X 3.14 X 2.1 m = 13.188 m, So length of the arc =  13.188 m ÷ 4 = 3.297 m.

Question 13.

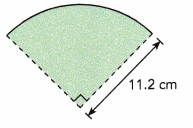
Answer:
Length of the arc = 17.584 cm,

Explanation:
Length of the arc of the quadrant = circumference ÷ 4 and C = πd or 2πr as given radius = 11.2 cm so circumfrence = 2 X 3.14 X 11.2 cm = 70.366 cm, So length of the arc =  70.366 cm ÷ 4 = 17.584 cm.

Find the distance around each semicircle. Use 3.14 as an approximation for π.

Question 14.

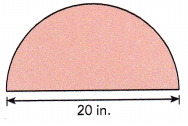
Answer:
Length of the semicircle = 31.4 in,

Explanation:
Length of semicircle = \(\frac{1}{2}\) X circumference, Given diameter d = 20 in as we know C = πd so length of semicircle is \(\frac{1}{2}\) X 3.14 X 20 in = 31.4 in.

Question 15.

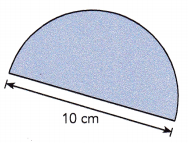
Answer:
Length of the semicircle = 31.4 in,

Explanation:
Length of semicircle = \(\frac{1}{2}\) X circumference, Given diameter d = 10 cm as we know C = πd so length of semicircle is \(\frac{1}{2}\) X 3.14 X 10 cm = 31.4 in.

Question 16.

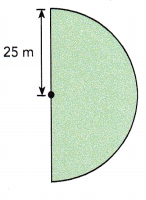
Answer:
Length of semicircle = 78.5 m,

Explanation:
Length of the semicircle = \(\frac{1}{2}\) X circumference and C = 2πr as given radius = 25 m so length of the semicircle = \(\frac{1}{2}\) X 2 X 3.14 X 25 m = 78.5 m.

Question 17.

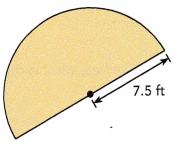
Answer:
Length of semicircle = 23.55 ft,

Explanation:
Length of the semicircle = \(\frac{1}{2}\) X circumference and C = 2πr as given radius = 7.5 ft so length of the semicircle = \(\frac{1}{2}\) X 2 X 3.14 X 7.5 ft = 23.55 ft.

Find the distance around each quadrant. Use \(\frac{22}{7}\) as an approximation for π.

Question 18.

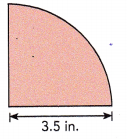
Answer:
Distance around quadrant = 5.495 in,

Explanation:
Distance of the quadrant = circumference ÷ 4 and C = πd or 2πr as given radius = 3.5 in. So circumfrence = 2 X 3.14 X 3.5 in = 21.98 in , So length of the quadrant =  21.98 in ÷ 4 = 5.495 in.

Question 19.

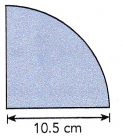
Answer:
Distance around quadrant = 16.485 cm,

Explanation:
Distance of the quadrant = circumference ÷ 4 and C = πd or 2πr as given radius = 10.5 cm so circumfrence = 2 X 3.14 X 10.5 cm = 65.94 cm, So length of the quadrant =  65.94 cm ÷ 4 = 16.485 cm.

Question 20.

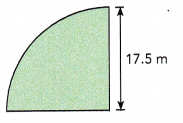
Answer:
Distance around quadrant = 27.475 m,

Explanation:
Distance of the quadrant = circumference ÷ 4 and C = πd or 2πr as given radius = 17.5 m so circumfrence = 2 X 3.14 X 17.5 m = 109.9 m , So length of the quadrant =  109.9 m ÷ 4 = 27.475 m.

Question 21.

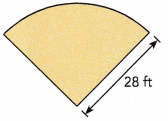
Answer:
Distance around quadrant = 43.96 ft,

Explanation:
Distance of the quadrant = circumference ÷ 4 and C = πd or 2πr as given radius = 28 ft so circumfrence = 2 X 3.14 X 28 ft = 175.84 ft, So length of the quadrant =  175.84 ft ÷ 4 = 43.96 ft.

Solve. Show your work. Use 3.14 as an approximation for π.

Question 22.
A circular garden has a diameter of 120 feet. Find its circumference.
Answer:
The circumfrence is 376.8 feet,

Explanation:
Given a circular garden has a diameter of 120 feet as we know circumference of circle is C = πd  given diameter = 120 feet so circumfrence = 3.14 X 120 ft = 376.8 feet.

Question 23.
A circular coaster has a radius of 4 centimeters. Find its circumference.
Answer:
The circumfrence is 25.12 cms,

Explanation:
Given a circular coaster has a radius of 4 centimeters as we know circumference of circle is C = 2πr given radius r = 4 cm so circumfrence = 2 X 3.14 X 4 cms =  25.12 cms.

Question 24.
The diameter of a roll of tape is 5\(\frac{1}{2}\) centimeters. Find its circumference.
Answer:
The circumfrence is 17.27 centimeters,

Explanation:
Given a diameter of a roll of tape 5\(\frac{1}{2}\) centimeters as we know circumference of circle is C = πd  given diameter = 5\(\frac{1}{2}\) centimeters so circumfrence = 3.14 X  5\(\frac{1}{2}\) centimeters = 3.14 X \(\frac{11}{2}\) centimeters = 17.27 centimeters.

Question 25.
The shape of a floor mat is a semicircle. Find the distance around the mat.

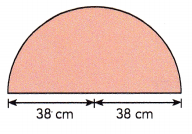
Answer:
Diatance around the mat = 119.32 cm,

Explanation:
Distance of semicircle = \(\frac{1}{2}\) X circumference, Given diameter d = 38 cm + 38 cm = 76 cm as we know C = πd so length of semicircle is \(\frac{1}{2}\) X 3.14 X 76 cm = 119.32 cm.

Question 26.
A small playground is shaped like a quadrant, as shown. Find the distance around the playground.

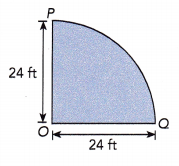
Answer:
The distance around the playground is 37.68 ft,

Explanation:
Given a small playground is shaped like a quadrant so distance of the quadrant = circumference ÷ 4 and C = πd or 2πr as given radius = 24 ft so circumfrence = 2 X 3.14 X 24 ft =150.72 ft, So length of the arc = 150.72 ft ÷ 4 = 37.68 ft.

Question 27.
If the radius of a wheel is 14 inches, what is the distance traveled when the wheel turns around 100 times?

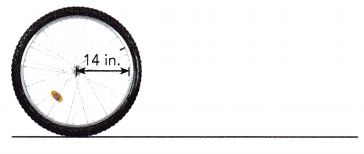
Answer:
The distance traveled when the wheel turns around 100 times is 8,792 inches,

Explanation:
Given the radius of a wheel is 14 inches, the distance traveled is circumference so it is C = πd or 2πr as given radius = 14 in so circumfrence = 2 X 3.14 X 14 inchs = 87.92 inches so the distance traveled when the wheel turns around 100 times is 100 X 87.92 inches = 8,792 inches.

Find the distance around each figure. Use \(\frac{22}{7}\) as an approximation for π.

Question 28.
The figure is made up of a rectangle and a semicircle.

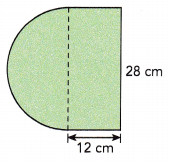
Answer:
Length of a rectangle is 80 cm,
Length of the semicircle = 43.96 cm,

Explanation:
Length or Perimeter of rectangle = 2(length + width) = 2(28 cm + 12 cm) = 2(40 cm) = 80 cm,
Length of semicircle = \(\frac{1}{2}\) X circumference, Given diameter d = 28 cm as we know C = πd so length of semicircle is \(\frac{1}{2}\) X 3.14 X 28 cm = 43.96 cm.

Question 29.
The figure is made up of an equilateral triangle and a semicircle.

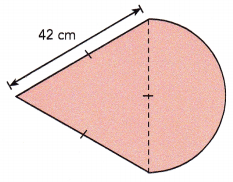
Answer:
Length of equilateral triangle =
Length of the semicircle = 65.94 cm,

Explanation:
Length of equilateral triangle = 42 cm + 42 cm + 42 cm = 126 cm,
Length of semicircle = \(\frac{1}{2}\) X circumference, Given diameter d = 42 cm as we know C = πd so length of semicircle is \(\frac{1}{2}\) X 3.14 X 42 cm = 65.94 cm.

Find the distance around each figure. Use 3.14 as an approximation for π.

Question 30.
The figure is made up of a rectangle and two identical semicircles.

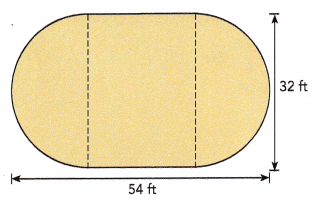
Answer:
Length of a rectangle is 172 ft,
The length of each identical semicircles is 50.24 ft,

Explanation:
Length or Perimeter of rectangle = 2(length + width) = 2(54 ft + 32 ft) = 2 X 86 ft = 172 ft,
Length of semicircle = \(\frac{1}{2}\) X circumference, Given diameter d = 32 ft as we know C = πd so length of semicircle is \(\frac{1}{2}\) X 3.14 X 32 ft = 50.24 ft.

Question 31.
The figure is made up of two identical quadrants, a semicircle, and an equilateral triangle.

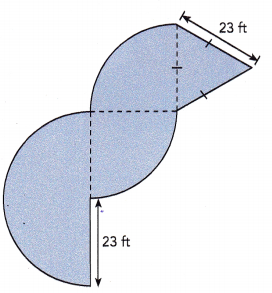
Answer:
The length of each quardrants is 36.11 ft,
The length of a semicircle is 72.22 ft,
Length of equilateral triangle is 69 ft,

Explanation:
Distance of the quadrant = circumference ÷ 4 and C = πd or 2πr as given radius = 23 ft so circumfrence = 2 X 3.14 X 23 ft = 144.44 ft, So length of the each quadrant = 144.44 ft ÷ 4 = 36.11 ft.
Length of semicircle = \(\frac{1}{2}\) X circumference, Given radius = 23 ft as we know C = 2πr so length of semicircle is \(\frac{1}{2}\) X 3.14 X 2 X 23 ft = 72.22 ft. Length of equilateral triangle is 23 ft + 23 ft + 23 ft = 69 ft.