Math in Focus Grade 6 Chapter 12 Lesson 12.3 Answer Key Volume of Prisms

This handy Math in Focus Grade 6 Workbook Answer Key Chapter 12 Lesson 12.3 Volume of Prisms detailed solutions for the textbook questions.

Math in Focus Grade 6 Course 1 B Chapter 12 Lesson 12.3 Answer Key Volume of Prisms

Math in Focus Grade 6 Chapter 12 Lesson 12.3 Guided Practice Answer Key

Find the volume of each rectangular prism.

Question 1.

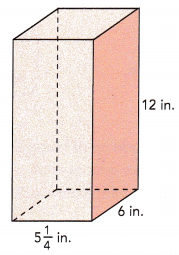
Length = 5\(\frac{1}{4}\) in.
Width = 6 in.
Height = 12 in.
V = lwh
= • •
= in.³
Answer:
V = lwh
Length = 5\(\frac{1}{4}\) in.
(5×\(\frac{4}{4}\)+\(\frac{1}{4}\)) = \(\frac{21}{4}\)
V = \(\frac{21}{4}\) × 6 × 12 = 378 cu.in

Question 2.

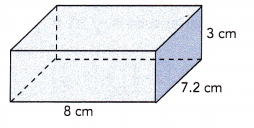
Length = 8 cm
Width = 7.2 cm
Height = 3 cm
V = lwh
= • •
= cm³
Answer:
V = 8 × 7.2 × 3
172.8 cu.cm

Question 3.

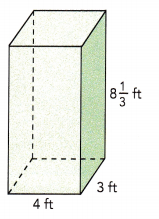
Length = 4 ft
Width = 3 ft
Height = 8 \(\frac{1}{3}\) ft
Volume =
= • •
= ft³
Answer:
V = lwh
Height = 8 \(\frac{1}{3}\) ft
(8 × \(\frac{3}{3}\))+\(\frac{1}{3}\) = \(\frac{25}{3}\)
Volume = 4×3×\(\frac{25}{3}\) = 100 cu.ft

Tell whether slices parallel to each given slice will form uniform cross sections. If not, explain why not.

Question 4.

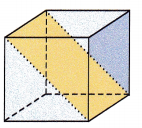
Answer:
No, in the above given figure, the slice parallel to each given slice will not form uniform cross-sections.
Because, the area of the cross-section is larger than the area’s of the cube’s face.

Question 5.

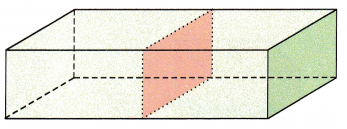
Answer:
In the above given figure, the slice parallel to each given slice will form uniform cross-sections.

Question 6.

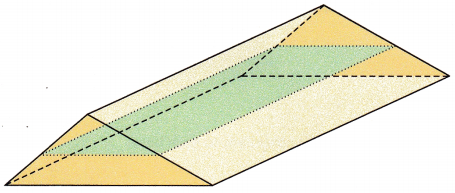
Answer:
No, in the above given figure, the slice parallel to each given slice will not form uniform cross-sections.
Because, the area of the cross-section is smaller than the area’s of the rectangular’s face.

Find the volume of each prism.

Question 7.

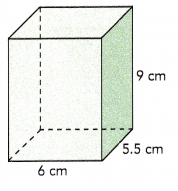
Length = 6 cm
Width = 5.5 cm
Height = 9 cm
Area of base = •
= cm²
Volume of prism = •
= cm²
The volume of the prism is cubic centimeters.
Answer:
Length = 6 cm
Width = 5.5 cm
Height = 9 cm
Area of base = 6×5.5 = 33 sq.cm
Volume of prism = Base area of prism × height
Volume of prism = 33×9 = 297 cu.cm
The volume of the prism is 297 cubic centimeters.

Question 8.

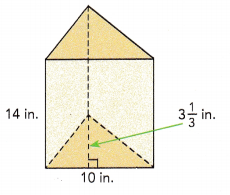
Base of triangle = 10 in.
Height of triangle = 3\(\frac{1}{2}\) in.
Height of prism = 14 in.
Area of base = \(\frac{1}{2}\) • •
= in.²
Volume of prism = •
= in.³
The volume of the prism is cubic inches.
Answer:
Base of triangle = 10 in.
Height of triangle = 3\(\frac{1}{2}\) in.
(3×\(\frac{2}{2}\))+\(\frac{1}{2}\) = \(\frac{7}{2}\)
Height of prism = 14 in.
Area of triangular base = \(\frac{1}{2}\) × base × height
Area of base = \(\frac{1}{2}\) × 10 × \(\frac{7}{2}\) = \(\frac{35}{2}\) sq.in
Volume of prism = Base area of prism × height
Volume of prism = \(\frac{35}{2}\) × 14 = 245 cu.in

Question 9.

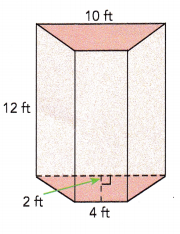
Length of shorter base of trapezoid = 4 ft
Length of longer base of trapezoid = 10 ft
Height of trapezoid = 2 ft
Height of prism = 12 ft
Area of base = \(\frac{1}{2}\) • ( + )
= \(\frac{1}{2}\) • •
= ft²
Volume of prism = •
= ft³
The volume of the prism is cubic feet.
Answer:
The formula to find the base area = \(\frac{1}{2}\) × height × (sum of parallel sides)
Area of base = \(\frac{1}{2}\) × 2 × (4+10)
= \(\frac{1}{2}\) × 2 × 14
= 14 sq.ft
Volume of prism = Base area of prism × height
Volume of prism = 14×12
= 168 cu.ft

Hands-On Activity

DETERMINING THE RELATIONSHIP BETWEEN VOLUME AND SURFACE AREA OF PRISMS

Materials:

• 27 unit cubes.

Work in pairs.
Step 1: Build the cube and the rectangular prism using unit cubes.

Step 2: Find the volume of the cube. Find the volume of the rectangular prism. What can you say about the volumes of the cube and the rectangular prism?
Answer:
Volume of cube = lwh
Volume of the cube = 2×2×2 = 8 cu.cm
Volume of the rectangular prism = 2×4×1 = 8 cu.cm
The volumes of the cube and the rectangular prism are same.

Step 3: Find the surface area of the cube. Draw its net if it helps you. Find the surface area of the rectangular prism. Draw its net if it helps you. What can you say about the surface areas of the cube and the rectangular prism?
Answer:
Area of one square will be 2×2 = 4 sq.cm
Volume of cuboid = 6 × Area of base
There are 6 faces for a cube, therefore the surface area will be 6×4 = 24 sq.cm
The surface areas of the rectangular prism will be 2(2×4 + 2×1 + 1×4) = 28 sq.cm
The surface areas of the cube and the rectangular prism are different.

Step 4: Now build these rectangular prisms using unit cubes.

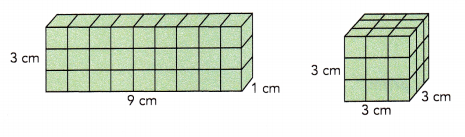
Step 5: Find the volume of the cube. Find the volume of the rectangular prism. What can you say about their volumes?
Answer:
Volume of the cube = 3×3×3 = 27 cu.cm
Volume of the rectangular prism = 3×9×1 = 27 cu.cm
The volumes of the cube and the rectangular prism are same.

Step 6: Find the surface area of the cube. Find the surface area of the . rectangular prism. Draw their nets if it helps you. What can you say about their surface areas?
Area of one square will be 3×3 = 9 sq.cm
There are 6 faces for a cube, therefore the surface area will be 6×9 = 54 sq.cm
The surface areas of the rectangular prism will be 2(3×9 + 9×1 + 1×3) = 78 sq.cm
The surface areas of the cube and the rectangular prism are different.

Math Journal Based on the activity, what can you conclude about prisms with the same volume? Discuss with your partner and explain your thinking.
Answer:
Two prisms of different measurements might have the same volume, they might not have the same surface area.
For example: A rectangular prism with side lengths of 1 cm, 2 cm, and 2 cm has a volume of 4 cu cm and a surface area of 16 sq cm. A rectangular prism with side lengths of 1 cm, 1 cm, and 4 cm has the same volume but a surface area of 18 sq cm

Math in Focus Course 1B Practice 12.3 Answer Key

Solve.

Question 1.
A cube has edges measuring 9 inches each. Find the volume of the cube.
Answer:
Given that: A cube has edges measuring 9 inches each.
The base area will be equal to 9×9=81 sq.in
Volume of cube = Area of base × height
Volume of the cube will be 81×9=729 cu.in

Question 2.
A cube has edges measuring 6.5 centimeters each. Find the volume of the cube.
Answer:
Given that: A cube has edges measuring 6.5 cm each.
The base area will be equal to 6.5×6.5=42.25 sq.cm
Volume of cube = Area of base × height
Volume of the cube will be 81×9=274.625 cu.cm

Question 3.
A storage container is shaped like a rectangular prism. The container is 20 feet long, 10 feet wide, and 5\(\frac{1}{2}\) feet high. Find the volume of the storage container.
Answer:
Given that: A rectangular prism is 20 feet long, 10 feet wide, and 5\(\frac{1}{2}\) feet high.
Area of base will be 20×10=200 sq.ft
Volume of prism = Area of base × height
Volume of the storage container will be 200×5\(\frac{1}{2}\)
= 200×(5×\(\frac{2}{2}\) + \(\frac{1}{2}\))
= 200×(\(\frac{10}{2}\) + \(\frac{1}{2}\))
= 200×\(\frac{11}{2}\)
= 100×11
= 1100 cu.ft

Question 4.
Find the volume of the peppermint tea box on the right.

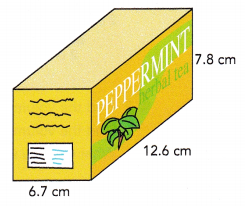
Answer:
Given that: The peppermint tea box is 12.6 cm long, 6.7 cm wide, and 7.8 cm high.
Area of  base will be 12.6×6.7 = 84.42 sq.cm
Volume of prism = Area of base × height
Volume of the box will be 7.8×84.42 = 658.476 cu.cm

Question 5.
The solid below is made of idential cubes. Each cube has an edge length of 2 inches. Find the volume of the solid.

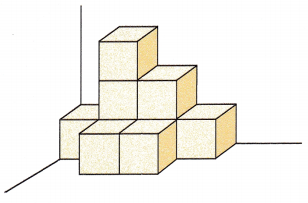
Answer:
Given that: Each cube has an edge length of 2 inches.
Let us first find the volume of a single cube
Area of the base of a single cube will be 2×2=4 sq.in
Volume of cube = Area of base × height
Volume of a single cube will be  4×2=8 cu.in
The given solid is made of idential cubes. There are 9 such cubes.
Therefore, the volume of all the 9 identical cubes or the given solid figure will be 9×8=72 cu.in

Find the volume of the triangular prism.

Question 6.

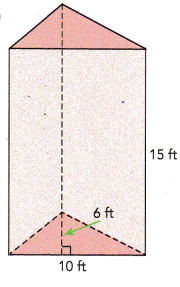
Answer:
Given that: A triangular prism is 15ft long, 10ft wide and 6ft high.
Area of the triangular prism = \(\frac{1}{2}\) × base × height
Area of the triangular prism will be \(\frac{1}{2}\) × 10 × 6
= 10 × 3
= 30 sq.ft
Volume of prism = Area of base × height
Volume of the given triangular prism will be 30×15=450 cu.ft

Question 7.

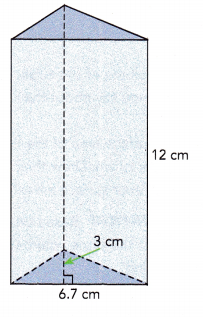
Answer:
Given that: A triangular prism is 12cm long, 6.7cm wide and 3cm high.
Area of the triangular prism = \(\frac{1}{2}\) × base × height
Area of the triangular prism will be \(\frac{1}{2}\) × 6.7 × 3
= \(\frac{1}{2}\) × 20.1
= 10.05 sq.cm
Volume of prism = Area of base × height
Volume of the given triangular prism will be 10.05×12=120.6 cu.cm

Tell whether slices parallel to each given slice will form uniform cross-sections. If not, explain why not.

Question 8.

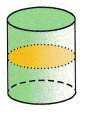
Answer:
In the above given figure, the slice parallel to each given slice will form uniform cross-sections.

Question 9.

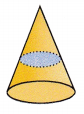
Answer:
No, in the above given figure, the slice parallel to each given slice will not form uniform cross-sections.
Because, the area of the cross-section is smaller than the area’s of the circular face.

Question 10.

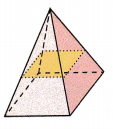
Answer:
No, in the above given figure, the slice parallel to each given slice will not form uniform cross-sections.
Because, the area of the cross-section is smaller than the area’s of the rectangular’s face.

Copy the solid. Draw a slice that has the same cross section as the bases In each prism.

Question 11.

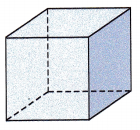
Answer:

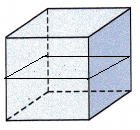
The bases for the above given figure is square.
Therefore, a slice that has the same cross section is drawn for the given prism.

Question 12.

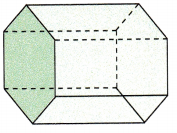
Answer:

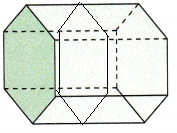
The bases for the above given figure is hexagon.
Therefore, a slice that has the same cross section is drawn for the given prism.

Question 13.

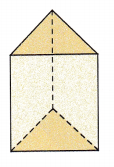
Answer:

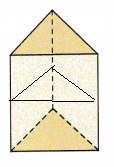
The bases for the above given figure is triangle.
Therefore, a slice that has the same cross section is drawn for the given prism.

Solve.

Question 14.
The bases of the prism shown are trapezoids. Find the volume of the prism.

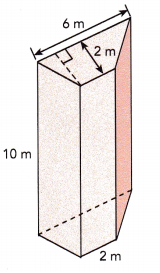
Answer:
Length of shorter base of trapezoid = 2 m
Length of longer base of trapezoid = 6 m
Height of trapezoid = 2 m
Height of prism = 10 m
The area of the given figure = \(\frac{1}{2}\) × height × (sum of parallel sides)
Area of base = \(\frac{1}{2}\) × 2 × (2+6)
= \(\frac{1}{2}\) × 2 × 8
= 8 sq.m
Volume of prism = base area × height
The volume of prism = 10×8
= 80 cu.m

Question 15.
A cube has a volume of 125 cubic inches. Find the length of its edge.
Answer:
Given that: A cube has a volume of 125 cu.in
Let us assume the length of a cube be ‘a’ unit.
As cube has all equal sides, the base area will be a×a = a² sq.units
Now, the volume will be a²×a = a³ cubic units.
Therefore we can say that the volume of a cube is the length of an edge taken to the third power.
a³ = 125 and 125 in cube can be written as 5³
a³ = 5³
a = 5
Therefore, the length of its edge will be 5 inches.

Question 16.
The volume of a triangular prism is 400 cubic centimeters. Two of its dimensions are given in the diagram. Find the height of a triangular base.

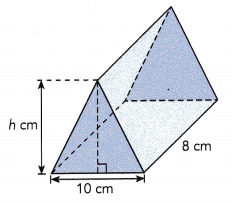
Answer:
Given that: The volume of a triangular prism is 400 cubic centimeters.
The three rectangular faces measures 10cm long and 8cm wide.

The area of three rectangular faces will be 3×10×8 = 240 sq.cm.
Inorder to get the areas of the triangular bases, we need to subtract the area of the rectangular faces from the total volume.
Area of two triangular bases will be 400-240 = 160 sq.cm
Area of one triangular base will be 160÷2 = 80 sq.cm
From the given figure, the base length of the triangle is 10 cm and the height is ‘h’ cm.
Area of triangular base = \(\frac{1}{2}\) × base × height
Area of the triangle is \(\frac{1}{2}\)×10×h = 80
5×h = 80
h = 80÷5
h = 16 cm.

Question 17.
A cross-section of the triangular prism shown below is parallel to a base. The area of the cross-section is 24 square feet. The ratio of DM to MA is 3 : 5 and the length of \(\overline{F O}\) is 6 feet. Find the volume of the triangular prism.

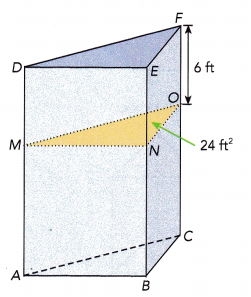
Answer:
Given that the area of cross-section is 24 sq.ft and ratio of DM to MA is 3 : 5.
The length of FO is 6 ft.
By observing the FO length and the ratio, we can say that the FO length is twice of the ratio of DM.
Therefore, the length of OC will be twice of the ratio of MA.
Length of OC = 10 ft.
Total length = FO + OC = 6+10 = 16 ft.
Volume of the triangular prism = Area of triangular base × length
Volume of the triangular prism = 24×16
Volume of the triangular prism = 384 cu.ft

Question 18.
The volume of the rectangular prism shown below is 2,880 cubic inches. The cross-section shown is parallel to a base. The area of the cross-section is 180 square inches. The length of \(\overline{A B}\) is x inches, and the length of \(\overline{B C}\) is 4x inches.
a) Find the length of \(\overline{A C}\).
Answer:
Given that: The volume of the rectangular prism is 2,880 cubic inches and the area of the cross-section is 180 square inches.
The length of AB is x inches and BC is 4x inches.
Length of AC will be AB+BC = x+4x = 5x

b) Find the value of x.

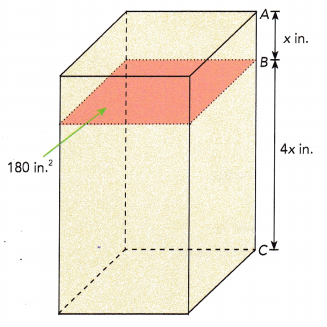
Answer:
Volume of the rectangular prism = 2,880 cubic inches
Volume of the rectangular prism = Area of rectangular base × length
2,880 = 180 × 5x
5x = 2880 ÷ 180
5x = 16
x = \(\frac{16}{5}\)
Length of AB will be \(\frac{16}{5}\) in.
Length of BC will be 4×\(\frac{16}{5}\) = \(\frac{64}{5}\) in.
Length of AC will be \(\frac{80}{5}\) = 16 in.

Question 19.
In the diagram of a cube shown below, points A, B, C, and D are vertices. Each of the other points on the cube is a midpoint of one of its sides. Describe a cross-section of the cube that will form each of the following figures.
a) a rectangle
b) an isosceles triangle
c) an equilateral triangle
d) a parallelogram

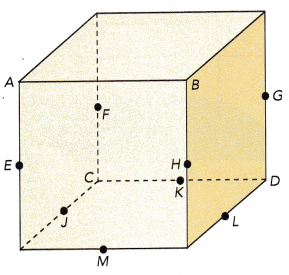
Answer:
a) a rectangle
By joining the CDLJ points, a rectangular cross section can be formed.
b) an isosceles triangle
By joining the MHL points, an isosceles triangle cross section can be formed.
c) an equilateral triangle
By joining the CDM points,an equilateral triangle cross section can be formed.
d) a parallelogram
By joining the MHGL points, a parallelogram cross section can be formed.

Solve. Use graph paper.

Question 20.
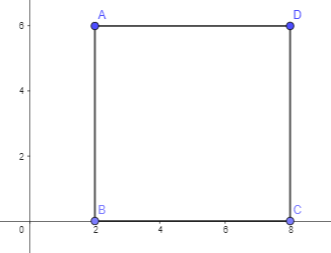
Points A, B, C, and D form a square. The area of the square is 9 square units.
a) Find the side length of square ABCD.
Answer:
Given that the area of the square is 9 square units.
Area of square = length × length
9 = length × length
3 × 3 = length × length
Length of the square will be 3 units.

b) The coordinates of point A are (2, 6). Points B and C are below \(\overline{A D}\). Point B is below point A, and point D is to the right of point A. Plot the points in a coordinate plane. Connect the points in order to draw square ABCD.
Answer:
The coordinates of point A are (2, 6).
Point B and C are below point A, so they will be (0,2) and C will be (0,8).
D will be (8,6)

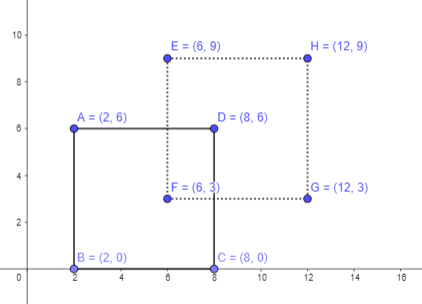
c) The points E, F, G, and H also form a square that is the same size as square ABCD. Point E is 4 units to the right of point A, and 3 units up. Points F and G are below \(\overline{E H}\). Point F is below point E, and point H is to the right of point E. Plot the points in the coordinate plane. Draw \(\overline{E H}\) and \(\overline{G H}\) with solid lines, and \(\overline{E F}\) and \(\overline{F G}\) with dashed lines.
Answer:
Point E is 4 units to the right of point A, and 3 units up. So, it will be (6,9).
Points F and G are below, so they will be (6,3) and (12,3).
Point H will be (12,9).

d) Draw \(\overline{A E}\), \(\overline{D H}\), and \(\overline{C G}\) with solid lines, and \(\overline{B F}\) with a dashed line, Use the solid and dashed lines to see the figure as a solid. Name the type of prism formed.
Answer:
After joining AE, DH, CG and BF.Below prism will be formed.
Since all the sides are of same length, it will form a cube.

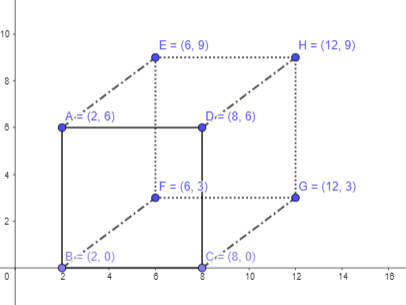
e) If the height of the prism is 7 units, find the volume of the prism.
Answer:
Area of the base 7×7 = 49 sq.units
Volume of the prism = 49×7 = 343 cu.units