Math in Focus Grade 6 Chapter 12 Lesson 12.2 Answer Key Surface Area of Solids

This handy Math in Focus Grade 6 Workbook Answer Key Chapter 12 Lesson 12.2 Surface Area of Solids detailed solutions for the textbook questions.

Math in Focus Grade 6 Course 1 B Chapter 12 Lesson 12.2 Answer Key Surface Area of Solids

Math in Focus Grade 6 Chapter 12 Lesson 12.2 Guided Practice Answer Key

Complete.

Question 1.
A cube has edges measuring 6 centimeters each. Find the surface area of the cube.

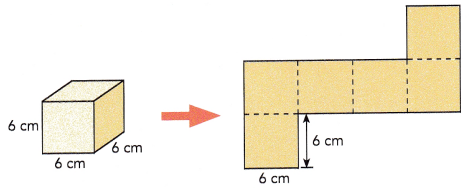
Area of one square face = •
= cm²
Surface area of cube = •
= cm²

Answer:
Each side of a square measures 6cm.
Area of a square base = length×length
Area of one square face = 6×6 = 36 sq.cm
Surface area of cube = Area of base × height
Surface area of cube = 36×6 = 216 sq.cm

Question 2.
A rectangular prism measures 7 inches by 5 inches by 10 inches. Find the surface area of the prism.

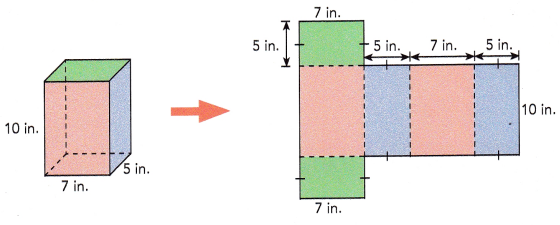
Total area of two orange and two purple faces = ( + + + ) •
= •
= in²
Area of two green rectangular bases = 2 • •
= in²
Surface area of rectangular prism = +
= in²

Answer:
Total area of two orange and two purple faces = (length + width + length + width)× height
Total area of two orange and two purple faces = (5+7+5+7)×10 = 24×10 = 240 sq.in
Area of rectangular base = length×width
Area of two green rectangular bases = 2×(5×7) = 70 sq.in
Surface area of rectangular prism = 240+70= 310 sq.in

Question 3.
The triangular prism shown has three rectangular faces. Its bases are congruent right triangles. Find the surface area of the triangular prism.

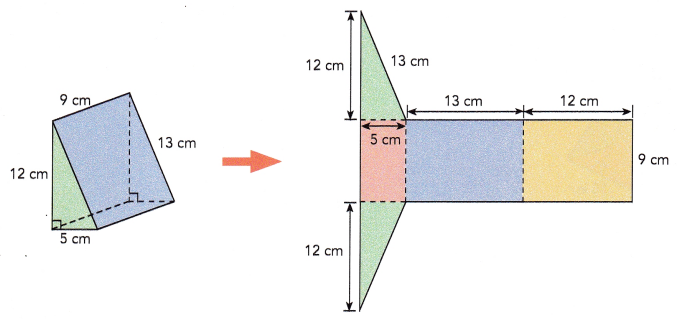
Total area of orange, purple, and yellow rectangles = ( + + ) •
= •
= cm²
Area of two green triangular bases = 2 • (\(\frac{1}{2}\) • • ) = cm²
Surface area of triangular prism = + = cm²
Answer:
Total area of orange, purple, and yellow rectangles = (length of three rectangles) × width
Total area of orange, purple, and yellow rectangles = (5+13+12)×9 = 30×9 = 270 sq.cm
Area of a triangle = \(\frac{1}{2}\) × base × height
Area of two green triangular bases = 2×(\(\frac{1}{2}\)×12×13) = 156 sq.cm
Surface area of triangular prism = 270+156 = 426 sq.cm

Question 4.
Alicia makes a pyramid that has an equilateral triangle as its base. The other three faces are congruent isosceles triangles. She measures the lengths shown on the net of her pyramid. Find the surface area of the pyramid.

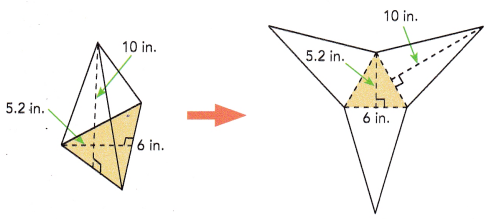
Area of yellow triangle = \(\frac{1}{2}\) • • = in.²
Area of three blue triangles = 3 • \(\frac{1}{2}\) • • = in.²
Surface area of triangular pyramid = + = in.²
Answer:
Area of a triangle = \(\frac{1}{2}\) × base × height
Area of yellow triangle = \(\frac{1}{2}\) × 5.2 × 6 = 15.6 sq.in
Area of three blue triangles = 3 × \(\frac{1}{2}\) × 10 × 6 = 90 sq.in
Surface area of triangular pyramid = 15.6 + 90 = 105.6 sq.in

Math in Focus Course 1B Practice 12.2 Answer Key

Solve.

Question 1.
A cube has edges measuring 6 centimeters each. Find the surface area of the cube.
Answer:
Measurement of each side of a cube is 6 cm.
Area of a square base= length×length
Surface area of one sqaure side will be 6×6 = 36 sq.cm
Surface area of a cube = 6×Area of base
A cube has 6 sides. Therefore, the total surface area will be 6×36 = 216 sq.cm
The surface area of cube will be 216 sq.cm.

Question 2.
The edge length of a cube is 3.5 inches. Find the surface area of the cube.
Answer:
Measurement of each side of a cube is 3.5 in.
Area of a square base= length×length
Surface area of one sqaure side will be 3.5×3.5 = 12.25 sq.in
Surface area of a cube = 6×Area of base
A cube has 6 sides. Therefore, the total surface area will be 6×12.25 = 75 sq.in
The surface area of cube will be 75 sq.in.

Question 3.
A closed rectangular tank measures 12 meters by 6 meters by 10 meters. Find the surface area of the tank.
Answer:
Total area of four rectangular faces = (length + width + length + width)× height
Total area of four rectangular faces = (12+6+12+6)×10 = 36×10 = 360 sq.m
Area of rectangle = length × width
Area of two rectangular bases = 2×(6×12) = 144 sq.m
Surface area of rectangular prism = 360+144= 504 sq.m

Question 4.
A closed rectangular tank has a length of 8.5 feet, a width of 3.2 feet, and a height of 4.8 feet. Find the surface area of the tank.
Answer:
Total area of four rectangular faces = (length + width + length + width)× height
Total area of four rectangular faces = (8.5+3.2+8.5+3.2)×4.8 = 23.4×4.8 = 112.32 sq.feet
Area of rectangle = length × width
Area of two rectangular bases = 2×(8.5×3.2) = 54.4 sq.feet
Surface area of rectangular prism = 112.32+54.4= 166.72 sq.feet

Question 5.
A triangular prism with its measurements is shown. Find the surface area of the prism.

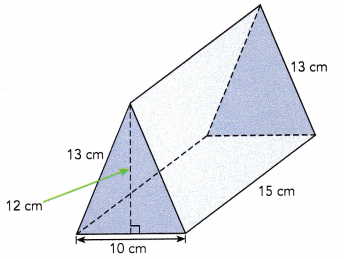
Answer:
Area of rectangle = length × width
Two rectangle measures 13 cm wide and 15 cm long. So, there area will be 2×13×15 = 390 sq.cm
Area of the third rectangle will be 15×10 = 150 sq.cm
Total area of three rectangular faces = 390+150 = 540 sq.cm
Area of triangle = \(\frac{1}{2}\)×base×height
Area of two triangular bases = 2×\(\frac{1}{2}\)×10×12 = 120 sq.cm
Surface area of triangular prism = 540+120 = 660 sq.cm

Question 6.
A triangular prism with its measurements is shown. Find the surface area of the prism.

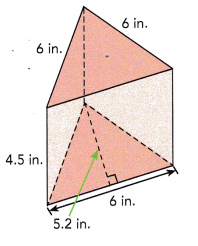
Answer:
Area of rectangle = length × width
Area of three rectangular faces = 3×6×4.5 = 81 sq.in
Area of triangle = \(\frac{1}{2}\)×base×height
Area of two triangular bases = 2×\(\frac{1}{2}\)×6×5.2 = 31.2 sq.in
Surface area of triangular prism = 81+31.2 = 112.2 sq.in

Solve.

Question 7.
A square pyramid has four faces that are congruent isosceles triangles. Find the surface area of the square pyramid if the base area is 169 square centimeters.

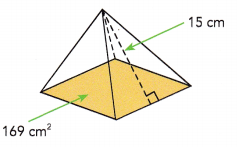
Answer:
The base area of the given figure is 169 sq.cm.
Since it is a square pyramid, the area will be side×side = 169 sq.cm
169 can also be written as 13 × 13
Therefore,  side × side = 13 × 13
Each side will be 13 cm.
Area of triangle = \(\frac{1}{2}\)×base×height
Area of four isosceles triangles faces = 4×\(\frac{1}{2}\)×13×15 = 390 sq.cm
Total surface area will be 169+390 = 559 sq.cm

Question 8.
The faces of this solid consist of four identical trapezoids and two squares. The side lengths of the two squares are 4 centimeters and 8 centimeters. The height of each trapezoid is 12 centimeters. Find the surface area of the solid.

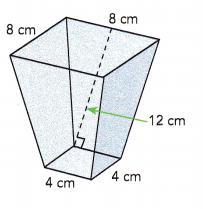
Answer:
Area of square = length×length
Area of first square = 4×4 = 16 sq.cm
Area of second square will be = 8×8 = 64 sq.cm
Total area of two squares base = 16+64 = 80 sq.cm
The formula to find the area of trapezium = \(\frac{1}{2}\) × height × (sum of parallel sides)
Area of four identical trapezoids = 4×\(\frac{1}{2}\) × (4+8) × 12
= 2 × 12 × 12
= 288 sq.cm
The surface area of the solid will be 80+288 = 368 sq.cm

Surface Area of a Trapezoidal Prism = h (b + d) + l (a + b + c + d) square units

Question 9.
Ms. Jones wants to paint the walls of a rectangular room. The height of the room is 8 feet. The floor is 10.5 feet wide and 12 feet long. The doors and windows total 24 square feet and are not going to be painted. Find the total area of the walls that need to be painted.
Answer:
The height of the room is 8 feet and the floor is 10.5 feet wide and 12 feet long.
Surface area of rectangular prism = 2×(length×width + width×height + height×length)
Area of the room will be = 2×(8×10.5 + 8×12 + 12×10.5)
168+192+252 = 612 sq.feet
The doors and windows total 24 square feet and are not going to be painted.As the doors and windows need not be painted, we can remove this area from the total area.
Therefore, the total area of the walls that need to be painted will be 612-24 = 588 sq.feet

Question 10.
The base of a prism has n sides. Write an expression for each of the following.
a) the number of vertices
Answer:
The number of vertices will be 2n.

b) the number of edges
Answer:
The number of edges will be 3n.

c) the number of faces
Answer:
The number of faces will be n+2

Question 11.
The base of a pyramid has m sides. Write an expression for each of the following.
a) the number of vertices
Answer:
The number of vertices will be m+1

b) the number of edges
Answer:
The number of edges will be 2m

c) the number of faces
Answer:
The number of faces will be m+1