Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 7 Lesson 7.4 Identifying Volumes of Composite Solids to score better marks in the exam.
Math in Focus Grade 7 Course 3 B Chapter 7 Lesson 7.4 Answer Key Identifying Volumes of Composite Solids
Math in Focus Grade 8 Chapter 7 Lesson 7.4 Guided Practice Answer Key
Solve.
Question 1.
A solid metal trophy is made up of a cylinder and a cone. The radius of the cylinder is equal to the radius of the cone. Find the volume of metal used to make the trophy. Round your answer to the nearest tenth. Use 3.14 as an approximation for π.
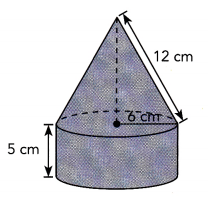
First find the height of the cone.
Let h represent the height of the cone in centimeters.

Then find the volume of the cone.
Volume = \(\frac{1}{3}\) • Area of base • Height
= ![]() Use the exact value of the height of the cone.
Use the exact value of the height of the cone.
≈ ![]() cm3
cm3
Next find the volume of the cylinder.
Volume = Area of base• Height
= ![]()
≈ ![]() cm3
cm3
Finally, find the volume of metal used.
Volume of metal used = Volume of cone + Volume of cylinder
≈ ![]() +
+ ![]()
= ![]() cm3
cm3
So, the volume of metal used is approximately ![]() cubic centimeters.
cubic centimeters.
Answer:
The volume of metal used is approximately 957 cubic centimeters,
Explanation:

Now the volume of cone
Volume = \(\frac{1}{3}\) • Area of base • Height,
Area of base is πr2 = 3.14 × 6 cm × 6 cm = 113.04 cm2,
V = Volume of cone = \(\frac{1}{3}\) • 113.04 • 10.39 = 391.495 cm2,
Given the radius of the cylinder is equal to the radius of the cone.
The volume of the cylinder =
Volume of cylinder = Area of base X height = 113.04 cm2 × 5 cm = 565.2 cm3,
Volume of metal used = Volume of cone + Volume of cylinder,
Volume of metal used = 391.495 cm3 + 565.2 cm3 = 956.695 cm3,
therefore the volume of metal used is approximately 957 cubic centimeters.
Math in Focus Course 3B Practice 7.4 Answer Key
For this practice, you may use a calculator. Use 3.14 as an approximation for n. Round your answer to the nearest tenth if necessary.
Question 1.
Find the volume of each of the following composite solids.
a) A triangular prism with a cylindrical hole cut out of it.
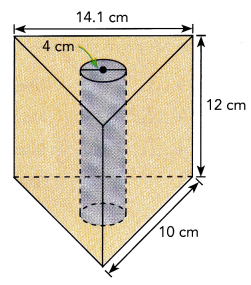
Answer:
Volume of triangular prism with a cylindrical hole cut out of it is 1089.12 cm3,
Explanation:
Volume of rectangular prism is width X height X length,
we have width 14.1 cm, height = 12 cm and length = 10 cm,
Volume of rectangular prism = 14.1 × 12 × 10 = 1,692 cm3,
Volume of cylinder =πr2h= 3.14 × 4 × 4 × 12 = 602.88 cm3,
therefore volume of triangular prism with a cylindrical hole cut out of it is
Volume of rectangular prism – Volume of cylinder =
1,692 cm3 – 602.88 cm3 = 1089.12 cm3.
b) A sphere connected to a cone that sits on top of a hemisphere.
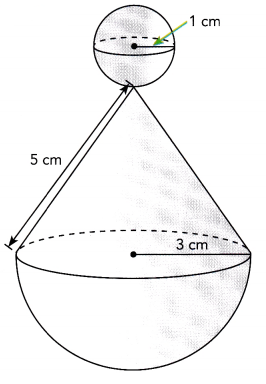
Answer:
Volume of sphere connected to a cone that sits on top of a hemisphere is 41.866 cm3,
Explanation:
First we calculate the volume of cone,
we calculate height of cone h2 + 32 = 52,
h2 = 25 – 9 = 16, so height of cone is square root of 16 which is 4,
Now volume of cone = \(\frac{1}{3}\) • 3.14 × 3 × 3 • 4,
Volume of cone = 37.68 cm3,
Volume of sphere = \(\frac{4}{3}\) • 3.14 × r3,
= \(\frac{4}{3}\) • 3.14 × 1 cm × 1 cm × 1 cm = 4.186 cm3,
therefore volume of sphere connected to a cone that sits on top of a hemisphere
= Volume of cone + Volume of sphere
= 37.68 cm3 + 4.186 cm3 = 41.866 cm3.
Question 2.
A ceramic candle holder in the shape of a cylinder has a radius of 2.40 inches. A hemisphere of radius 1.75 inches is removed from the center of the cylinder. Find the volume of ceramic in the candle holder.
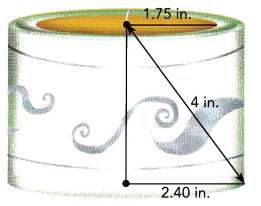
Answer:
The volume of ceramic in the candle holder is 27.104 in3,
Explanation:
Given a ceramic candle holder in the shape of a cylinder has a radius of 2.40 inches.
Now we caluculate height of cylinder using pythagorean theroem
2.402 + h2 = 42,
h2 = 16 – 5.76 = 10.24, the height is square root of 10.24 is 3.2 in
h = 3.2 in now volume of cylinder is 3.14 × r2 × h = 3.14 × 2.4 × 2.4 × 3.2 = Volume of cylinder is 57.876 in3,
As a hemisphere of radius 1.75 inches is removed from the center of the cylinder, the volume removed is 3.14 × 1.75 × 1.75 × 3.2 = 30.772 in3,
therefore the volume of ceramic in the candle holder is
volume of cylinder – volume of removed
= 57.876 in3 – 30.772 in3 = 27.104 in3.
Question 3.
A tent has a conical roof and a cylindrical wall as shown. The cylindrical wall and the conical roof are of the same height. The radius of the tent is 9 meters. Ropes are used to tie the tent to the ground.
a) Find the height of the wall.
Answer:
The height of the wall is 1.5 m,
Explanation:
Using pythogorean theorem the height h of the wall =
h2 + 0.82 = 1.72,
h2 = 2.89 – 0.64 = 2.25
so height is square root of 2.25 is 1.5 m.
b) Find the volume of space inside the tent.
Answer:
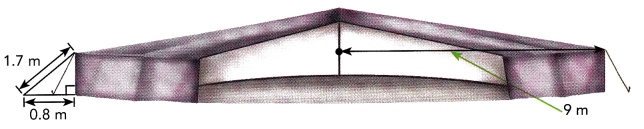
The volume of space inside the tent is 508.68 m3,
Explanation:
First we calculate the volume cylindrical walls as
3.14 × r2 × h = 3.14 × 9 × 9 × 1.5 = 381.51 m3,
Now volume conical roof is \(\frac{1}{3}\) • 3.14 × r × r • h,
\(\frac{1}{3}\) • 3.14 × 9 × 9 • 1.5 = 127.17 m3,
therefore the volume of space inside the tent is
381.51 m3 + 127.17 m3 = 508.68 m3.
Question 4.
A traffic cone is made up of a cone fixed on top of a square prism base with a height of 1 inch. Find the volume of the traffic cone.
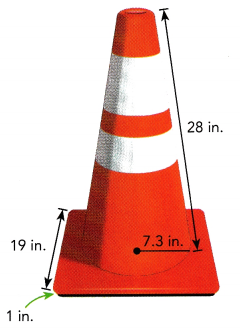
Answer:
The volume of the traffic cone is 1561.75 in3,
Explanation:
Given a traffic cone is made up of a cone fixed on top of a square prism base with a height of 1 inch with radius 7.3 in and height 28 in,
So volume of the traffic cone is \(\frac{1}{3}\) • 3.14 × r × r • h =
\(\frac{1}{3}\) • 3.14 × 7.3 × 7.3 × 28 = 1561.75 in3.
Question 5.
A sculpture is made out of a cone resting on top of a hemisphere. The hemisphere has a radius of 1 meter. Use the information in the diagram below to find the volume of the sculpture.
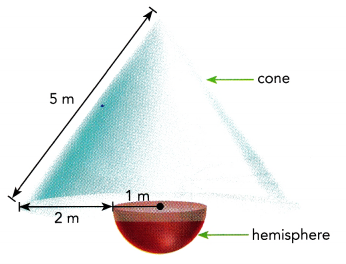
Answer:
Volume of sculpture is 37.68 m3,
Explanation:
Given a sculpture is made out of a cone resting on top of a hemisphere.
The hemisphere has a radius of 1 meter. Radius of cone is 2 m+ 1 m = 3 m,
applying phthagorean theorem to find height of cone
h2 + 32 = 52,
h2 = 25 – 9 = 16, h is square root of 16 is 4 m now volume of sculputure is
\(\frac{1}{3}\) • 3.14 × r × r • h
= \(\frac{1}{3}\) • 3.14 × 3 m × 3 m × 4 m
= 37.68 m3.
Question 6.
A trophy is made of a glass triangular prism attached to a 0.5 inch high wooden block shaped like a square prism. The height of the trophy is 6 inches. The volume of the wooden base is 4.5 cubic inches. Find the volume of the entire trophy, including the base.
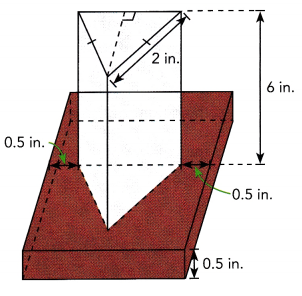
Answer:
Explanation:
Given a trophy is made of a glass triangular prism attached to a 0.5 inch high wooden block shaped like a square prism.
The height of the trophy is 6 inches.
The volume of the wooden base is 4.5 cubic inches.
Let x be the equal length of each side of the square ,
then the volume of the block will be 0.5 × x2 = 4.5,
x2 = 9 , so x is square root of 9 is 3,
The area of each triangular face of the prism will be 1/2 × 3 × 6 = 9.
The volume of the triangular prism will be 9 × 3 = 27 cubic inches.
The total volume will be 4.5 + 27 = 31.5 cubic inches.
Question 7.
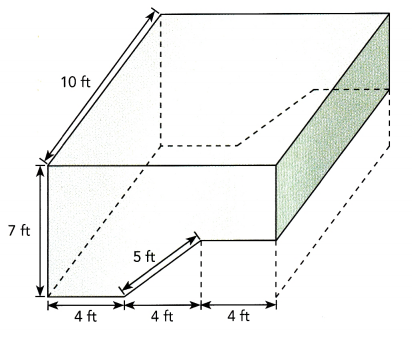
A swimming pool is 12 feet long and 10 feet wide. At its deepest, it is 7 feet deep. A slope 5 feet long links the deep end to the shallow end. Jonathan wants to fill the pool with 800 cubic feet of water. Is this possible? Explain.
Answer:
Yes, it is possible that the volume of the pool is exactly 800 cubic feet which will allow the 800 cubic feet of water to completely fill it,
Explanation:
The minimum volume of the pool is 12 × 10 × 2 = 240 cubic feet and
the maximum volume of the pool is 12 × 10 × 7 = 840 cubic feet.
since 800 cubic feet is somewhere between 240 and 840 cubic feet than 800 cubic feet of water could fill the pool.
To fill the pool with exactly 800 cubic feet of water, the sloped section would have to have a cross section of a
right triangle where the vertical leg would have to be .4206601574 feet and the horizontal leg would have to be 4.982273079 feet and the hypotenuse would have to be 5 feet.
The slope of 5 feet in length that links the deep end of the pool to the shallow end of the pool if the hypotenuse of this right triangle.
The formula for the volume of the pool would be
10 × 12 × (7 – .4206601574) + 10 × 1/2 × .420601574 × 4.982273079 = 800 cubic feet.
So, if the minimum depth of the pool is 6.579339843 feet and the sloped section of the pool is 5 feet and the horizontal distance of the sloped section of the pool is 4.982273079 feet, and the maximum depth of the pool is 7 feet, then the volume of the pool will be exactly 800 cubic feet.
The area of this vertical cross section will be 80 square feet.
The volume of the pool will be 10 × the area of the vertical cross section, making the volume equal to 800 cubic feet.
Yes it is possible that the volume of the pool is exactly 800 cubic feet which will allow the 800 cubic feet of water to completely fill it.
Question 8.
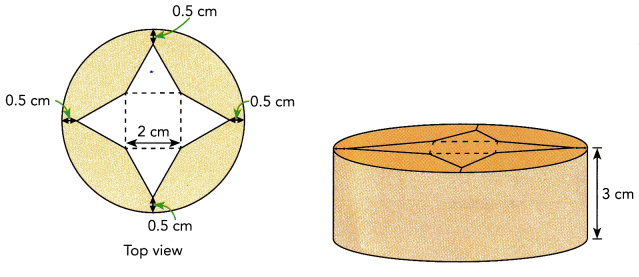
A crystal paperweight is shaped like a cylinder with a star-shaped hole. The top of the star-shaped hole is shaped like a square with four points that are identical equilateral triangles. The height of the cylinder is 3 centimeters. Find the volume of the paperweight.
Answer:
There is far too little information given. In addition to the height of the cylinder, we need to know its radius, along with the lengths of the sides of the square and equilateral triangles.
Question 9.
Math Journal The solid shown below is made of a cylinder with two identical cones at the ends of the cylinder. Linda says that if the radius of the cylinder is doubled, the volume of the solid will also be doubled. Is she correct? Why?

Answer:
Linda is not correct,
Explanation:
Let radius of cylinder = r ,
Then, volume of cylinder is given by V = πr2h,
According to the question, now Radius of the cylinder = 2r
Then, volume of cylinder is given by V’ = π(2r)2h = 4πr2h =4 (πr2h) = 4V ⇒ V’ = 4V ,
Thus, volume will be four times more if the radius of a cylinder is doubled.
Linda is not correct because it becomes four times more.
Brain @ Work
Question 1.
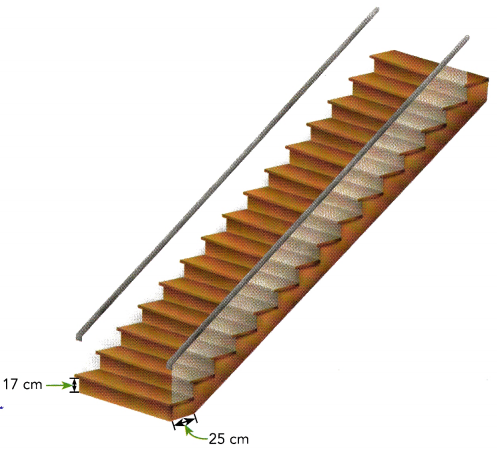
An architect designs a staircase for a new house. There will be 14 steps, and each step will be 17 centimeters high and 25 centimeters wide. The architect will build a railing on both sides of the steps. Find the total length needed for the two railings, not including any vertical support posts.
Answer:
The goal is to find the measure of the railings for the both sides of the staircase if the stairs have 14 steps and the steps are 17 centimeters in height and 25 centimeters in width.
Observe that the width, height and the railings of the staircase forms a right triangle. To determine the height and the width of the stairs, multiply the 14 steps to the measure of the riser and the measure of the width of the steps. For the height, 14 multiplied by 17 is 238 whiLe the product of 14 and 25 is 350 will be the width. Then appLying the Pythagorean Theorem which equates the square of the hypotenuse to the sum of the squares of the legs, the length of the railings can be computed represented by y which serves as the hypotenuse.
2382 + 3502 = y2 Use Pythagorean Theorem.
56, 644 + 122, 500 = y2 Multiply.
179, 144 = y2 Add.
y = \(\sqrt{179,144}\) Find positive square root.
y ≈ 423.3 Simplify.
Therefore, the measure of the two railings are 423.3 centimeters.
Question 2.
The Colorado river is about 210 meters wide. Brad and John start swimming from the same bank. Brad swims 215 meters against the current to reach a point on the opposite bank. Brad’s swimming speed is greater than the speed of the current. John swims 220 meters with the current to reach another point on the opposite bank. Find the distance between the two points.
Answer:
First, for better understanding, illustrate the situation of John and Brad Let A be the starting point of Brad and John, B be the corresponding point of A in the opposite side of the river, C be the position of Brad on the other side of the river after he swims, and D be John’s position after swimming Since Brad swims opposite the current while John swims along with the current, then they went on the opposite side of one another to reach the other side of the river.
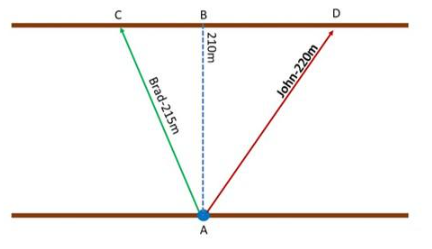
Notice that, the distance of the John and Brad can be computed by adding the distance of \(\overline{C B}\) and \(\overline{D B}\). Also, the measure of \(\overline{C B}\) and \(\overline{D B}\) can be solved by applying Pythagorean Theorem since \(\overline{A B}\), \(\overline{A C}\), and \(\overline{C B}\) creates a right triangle and \(\overline{A B}\), \(\overline{A D}\), and \(\overline{D B}\) form another right triangle.
For \(\overline{A B}\), \(\overline{A C}\), and \(\overline{C B}\) Let \(\overline{A C}\) be the hypotenuse and the other lines be the Legs. Note that Pythagorean Theorem states that the square of the hypotenuse is equal to the sum of the squares of the legs of a right triangle then
\(\overline{A B}^{2}+\overline{C B}^{2}=\overline{A C}^{2}\) Use the Pythagorean Theorem.
2102 + \(\overline{C B}^{2}\) = 2152 Substitution.
44. 100 + \(\overline{C B}^{2}\) = 46,225 Multiply.
\(\overline{C B}^{2}\) = 2, 125 Subtract 44.100 to both sides.
\(\overline{C B}\) = \(\sqrt{2,125}\) Find the positive square root.
\(\overline{C B}\) ≈ 46.1 Simplify.
Therefore, \(\overline{C B}\) measures about 46.1 meters.
Next, for \(\overline{A B}\), \(\overline{A D}\), and \(\overline{D B}\), let \(\overline{A D}\) be the hypotenuse and the remaining sides are the [egs then apply the Pythagorean Theorem again.
\(\overline{A B}^{2}+\overline{D B}^{2}=\overline{A D}^{2}\) Use the Pythagorean Theorem.
2102 + \(\overline{D B}^{2}\) = 2202 Substitution
44, 100 + \(\overline{D B}^{2}\) = 48, 400 Multiply.
\(\overline{D B}^{2}\) = 4,300 Subtract 44,100 to both sides.
\(\overline{D B}\) = \(\sqrt{4,300}\) Find the positive square root.
\(\overline{D B}\) ≈ 65.6 Simplify.
Therefore, \(\overline{D B}\) measures around 65.6 meters.
Lastly, add the two distances to determine the distance of John and Brad to one another.
46.1 + 65.6 = 111.7
Therefore, Brad and John are 111.7 meters away from one another.