Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 6 Review Test to score better marks in the exam.
Math in Focus Grade 7 Course 2 B Chapter 6 Review Test Answer Key
Concepts and Skills
Tell whether each pair of angles are supplementary, complementary or neither.
Question 1.
m∠1 = 23° and m∠2 = 157°
Answer:
Explanation:
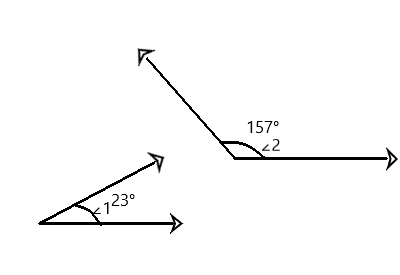
Question 2.
m∠3 = 65° and m∠4 = 25°
Answer:
Explanation:
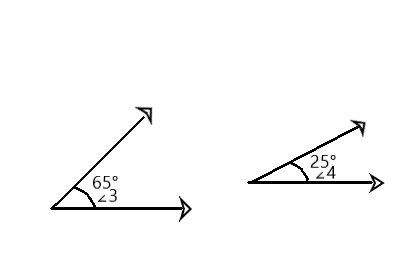
Question 3.
m∠5 = 43° and m∠6 = 57°
Answer:
Explanation:
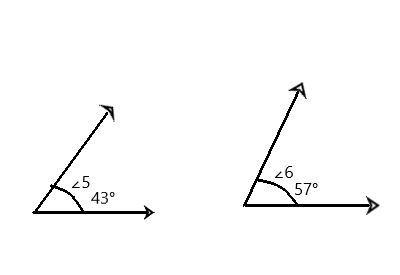
Question 4.
m∠7 = 82° and m∠8 = 8°
Answer:
Explanation:
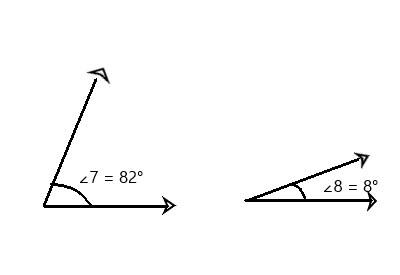
Question 5.
m∠9 = 110° and m∠10 = 80°
Answer:
Explanation:
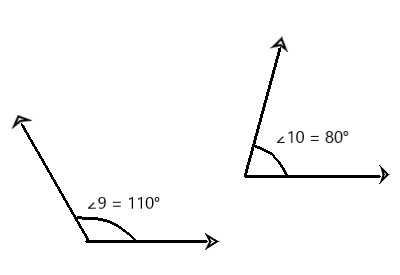
Question 6.
m∠11 = 18° and m∠12 = 62°
Answer:
Explanation:
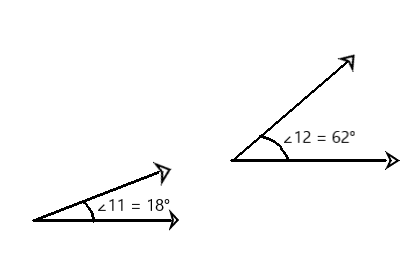
Tell whether the following list of angle measures are complementary or supplementary.
m∠A = 67°, m∠B = 80°, m∠C = 131°, m∠D = 21°,
m∠E = 51°, m∠F = 46°, m∠G = 10°, m∠H = 120°,
m∠J = 69°, m∠K = 60°, m∠P = 49°, m∠Q = 113°,
m∠R = 44°, m∠S = 41°
Question 7.
Name two pairs of complementary angles.
Answer:
m∠B = 80°, m∠G = 10°
m∠F = 46°, m∠R = 44°
Explanation:
Two angles are called complementary when the measures of their angles add to 90 degrees. The two pairs of complementary angles are m∠B = 80°, m∠G = 10°. If we add both angles the sum adds up to 90°.
Question 8.
Name two pairs of supplementary angles.
Answer:
m∠A = 67°, m∠Q = 113°
m∠H = 120°, m∠K = 60°
Explanation:
Two angles are called supplementary when the measures of their angles add to 180 degrees. The two pairs of supplementary angles are m∠A = 67°, m∠Q = 113°. If we add both angles the sum adds up to 180°.
Copy and complete.
Question 9.
Name two pairs of angles for each type of angle pair.

Answer:
∠TBC = 60°, ∠ABR = 30° are complementary angles.
∠RBT = 120°, ∠TBC = 60°are supplementary angles.
Explanation:

The two pairs of angles for complementary angles are ∠TBC = 60°, ∠ABR = 30°.
The two pairs of angles for supplementary angles are ∠RBT = 120°, ∠TBC = 60°
Find the measure of each numbered angle.
Question 10.
\(\overleftrightarrow{\mathrm{AB}}\) is a straight line.
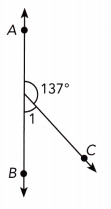
Answer:
The measurement of numbered angle 1 is 43°.
Explanation:
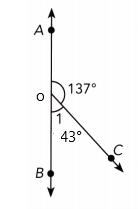
∠AOC + ∠BOC = 180°
1 + 137° = 180°
1 = 180° – 137°
1 = 43°
Question 11.
\(\overleftrightarrow{\mathrm{AB}}\) is a straight line.
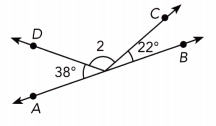
Answer:
The measurement of numbered angle 2 is 120°.
Explanation:
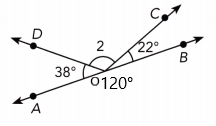
∠AOD + ∠DOC + ∠COB = 180°
38° + 2 + 22° = 180°
2 + 60° = 180°
2 = 180° – 60°
2 = 120°
Find the measure of each numbered angle.
Question 12.
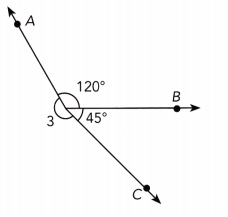
Answer:
The measurement of numbered angle 3 is 195°
Explanation:
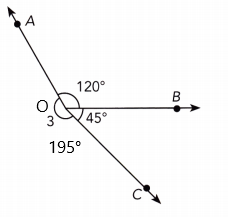
∠AOB + ∠COB + ∠AOC = 360°
3 + 120°+ 45° = 360°
3 + 165° = 360°
3 = 360° – 165°
3 = 195°
Question 13.
\(\overleftrightarrow{\mathrm{AB}}\) is a straight line.
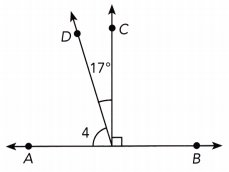
Answer:
The measurement of numbered angle 4 is 73°
Explanation:
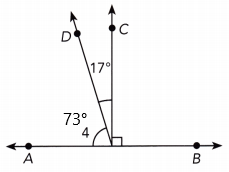
∠AOD + ∠DOC + ∠COB = 180°
4 + 17° + 90° = 180°
4 + 107° = 180°
4 = 180° – 107°
4 = 73°
Use an equation to find the value of each variable.
Question 14.
\(\overleftrightarrow{\mathrm{AB}}\) is a straight line.
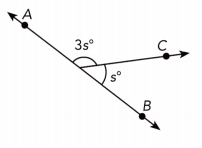
Answer:
s°= 45°, 3s°= 135°
Explanation:
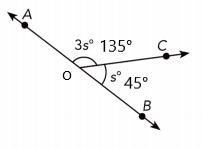
∠AOC + ∠COB = 180°
3s° + s° = 180°
4s° = 180°
s° = 180 ÷ 4
s° = 45°
3s°= 135°
Question 15.
\(\overleftrightarrow{\mathrm{AB}}\) is a straight line.
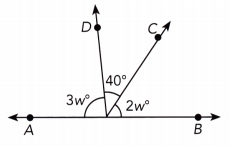
Answer:
w° = 28°, 2w° =56°, 3w°=140°
Explanation:
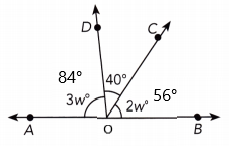
∠AOD + ∠DOC + ∠COB = 180°
3w° + 40° + 2w° = 180°
5w° + 40° = 180°
5w° = 180° – 40°
5w° = 140°
w° = 28°
3w°= 3 × 28 = 84°
2w°= 2° × 28 = 56°
Question 16.
\(\overleftrightarrow{\mathrm{AB}}\) is a straight line.
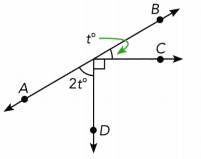
Answer:
t° = 30°, 2t° = 30°
Explanation:
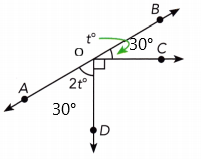
∠BOC + ∠AOD + ∠DOC = 180°
t° + 2t° + 90° = 180°
3t° + 90° = 180°
3t° = 180° – 90°
3t° = 90°
t° = 90° ÷ 3
t° = 30°
Question 17.
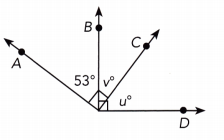
Answer:
v°=17°, u°=73°
Explanation:
∠AOB + ∠BOC = 90°
53° + v° = 90°
v° = 90° – 53°
v° = 17°
∠BOC + ∠COD = 90°
v° + u° = 90°
17° + u° = 90°
u° = 90° – 17°
u° = 73°
Question 18.
\(\overleftrightarrow{\mathrm{AB}}\), \(\overleftrightarrow{\mathrm{CD}}\), and \(\overleftrightarrow{\mathrm{EF}}\) are a straight line.
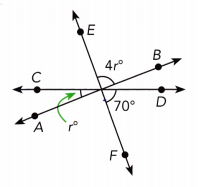
Answer:
r°= 22°, 4r°= 88°
Explanation:
∠COA = ∠BOD = r° (vertically opposite angles)
∠EOB + ∠BOD + ∠FOD = 180°
4r° + r° + 70° = 180°
5r° + 70° = 180°
5r° = 180° – 70°
5r° = 110°
r° = 110 ÷ 5
r° = 22°
4r° = 4 × 22 = 88°
Question 19.
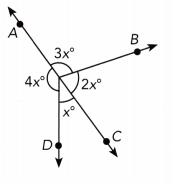
Answer:
x° = 36°, 2x° = 72°, 3x° = 108°, 4x° = 144°
Explanation:
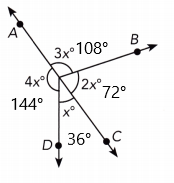
3x° + 2x° = 180°
5x° = 180°
x° = 180÷5
x° = 36°
2x° = 36 × 2 = 72°
3x° = 3 × 36 = 108°
4x° = 4 × 36 = 144°
\(\overline{M N}\) is parallel to \(\overline{P Q}\). Find the measure of each numbered angle.
Question 20.
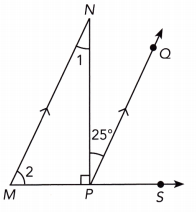
Answer:
∠1 = 25°, ∠2 = 65°, x° = 65°
Explanation:
Let ∠QPS = x°
∠NPM + ∠NPQ + ∠QPS = 180°
90° + 25° + x° = 180°
115° + x° = 180°
x° = 180 -115°
x° = 65°
∠2 = ∠x = 65° Corresponding angles are equal
∠NMP + ∠PNM = 90°
∠2 + ∠1 = 90°
65° + ∠1 = 90°
∠1 = 90° – 65°
∠1 = 25°
Question 21.
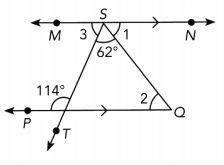
Answer:
∠1 = 52°, ∠2 = 52°, ∠3 = 66°
Explanation:
Let ∠SOQ = x°
114°+ x° = 180°
x° = 180° – 114°
x° = 66°
x° = ∠3 = 66° (vertically opposite angles)
∠3 + ∠TSQ + ∠QSN = 180°
∠3 + 62° + ∠2 = 180°
66° + 62° + ∠2 = 180°
∠2 = 180° – 128°
∠2 = 52°
∠1 = ∠2 (vertically opposite angles)
∠1 = 52°
Problem Solving
Solve. Show your work.
Find the value of x.
Question 22.
Find the value of x.
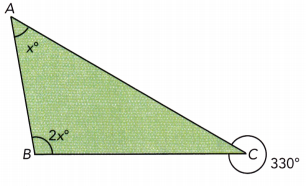
Answer:
x° + 2x° = 330°
3x°= 330°
x° = 330 ÷ 3
x° = 110°
Question 23.
ABCD is a rhombus. Find the measures of ∠1 and ∠2.
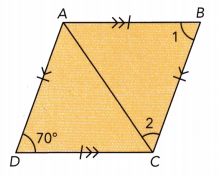
Answer:
∠1 = 70°, ∠2 = 120°
Explanation:
Opposite angles in a rhombus are equal.
∠1 = 70°
∠1 + ∠2 + 70° = 360°
70° + ∠2 + 70° = 360°
∠2 + 140° = 360°
∠2 = 360° – 140°
∠2 = 120°
Question 24.
ABCD is a rectangle. \(\overline{\mathrm{AE}}\) and \(\overline{\mathrm{DC}}\) are straight lines. ∠FBG is a right angle, m
ABF = 74°, and m∠BEG = 42°. Find the measures of ∠EBG and ∠BGC.
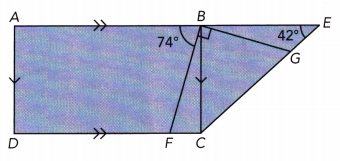
Answer:
x=∠EBG =16°, ∠BGC = 122°
Explanation:
74° + 90° + x° = 180°
x° = 180° – 164°
x° = 16°
16° + 42° + ∠BGC = 180°
∠BGC = 180° – 58°
∠BGC = 122°
Question 25.
The diagram shows the flag of the United Kingdom. m∠MNR = 90°. Name two pairs of complementary and supplementary angles.
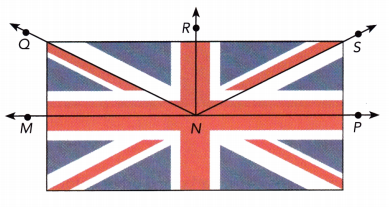
Answer:
∠MNQ, ∠SNP, ∠QNS are complementary angles.
∠MNR, ∠MNQ, ∠SNP are supplementary angles.
Explanation:
The two pairs of angles for complementary angles are ∠MNQ, ∠SNP, ∠QNS.
The two pairs of angles for supplementary angles are ∠MNR, ∠MNQ, ∠SNP.
Question 26.
m∠1 = 15° and m∠2 = 131°. \(\overleftrightarrow{\mathrm{AB}}\) is a straight line. Find the measure of ∠3.

Answer:
∠3 = 34°
Explanation:
m∠1 + m∠2 + m∠3 = 180°
15° + 131° + m∠3 = 180°
m∠3 + 146° = 180°
m∠3 = 180° – 146°
m∠3 = 34°
Question 27.
The diagram shows ∠1 and ∠2, which are formed by \(\overleftrightarrow{M N}\) intersecting \(\overleftrightarrow{P Q}\) and \(\overleftrightarrow{R S}\). In the diagram, m∠1 = (12x + 7)°, m∠2 = (10x + 15)°, and x = 4. Explain how you know that \(\overleftrightarrow{P Q}\) is parallel to \(\overleftrightarrow{R S}\).
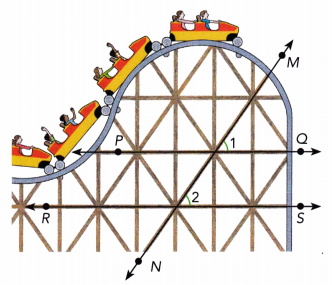
Answer:
Parllel lines are lines that are always the same distance apart and will never intersect. Hence in the given figure the lines \(\overleftrightarrow{P Q}\) is parallel to \(\overleftrightarrow{R S}\).
And iif two lines are parllel the corresponding angles are equal. Therefore ∠1 = ∠2
Explanation:
m∠1 = m∠2 are corresponding angles
(12x + 7)° = (10x + 15)°
12x – 10x = 15 – 7
2x = 8
x° = 8 ÷ 2
x° = 4°
(12x + 7)° = 12 × 4 + 7 = 48 + 7 = 55°
(10x +15)° = 10 × 4 + 15 = 40 + 15 = 55°
Question 28.
In the diagram, m∠1 = (5x – 20)°, m∠2 = (2x + 14)°, and m∠3 = 18°. Use an equation to find the measures of ∠1 and ∠2.
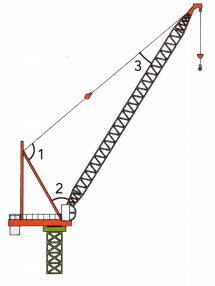
Answer:
∠1 = 100°, ∠2 = 62°, ∠3 = 24°
Explanation:
m∠1 + m∠2 + m∠3 = 180°
(5x – 20)° + (2x + 14)° + 18° =180°
7x – 6 + 18° = 180°
7x +12 = 180°
7x = 180° – 12°
7x = 168°
x°= 24°
5x – 20 = 5 × 24 – 20 = 120 – 20 =100°
2x + 14 = 2 × 24 + 14 = 62°
∠1 = 100°, ∠2 = 62°, ∠3 = 24°