Math in Focus Grade 8 Chapter 7 Lesson 7.3 Answer Key Understanding the Pythagorean Theorem and Solids

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 7 Lesson 7.3 Understanding the Pythagorean Theorem and Solids to score better marks in the exam.

Math in Focus Grade 7 Course 3 B Chapter 7 Lesson 7.3 Answer Key Understanding the Pythagorean Theorem and Solids

Math in Focus Grade 8 Chapter 7 Lesson 7.3 Guided Practice Answer Key

Solve.

Question 1.
The radius of a cone-shaped hat is 5 centimeters. The slant length of the hat is 8 centimeters. What is the height of the hat? Round your answer to the nearest tenth.

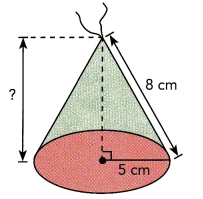
Let the height be x centimeters.

So, the height of the hat is approximately centimeters.
Answer:
The height of the hat is approximately 6 centimeters,

Explanation:

Solve.

Question 2.
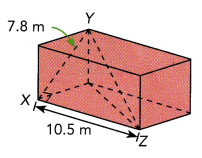
Given the diagonal length, XY, of the end wall of the King’s Chamber of the Great Pyramid and the length, XZ, of the chamber, find the length, YZ, of the central diagonal. Find both the exact value and the approximate value to the nearest tenth.

+ = YZ² Use the Pythagorean Theorem.
+ = YZ² Substitute values for \(\overline{X Y}\) and \(\overline{X Z}\).
+ = YZ² Multiply.
= Add.
= YZ Find the positive square root.
YZ ≈ m Round to the nearest tenth.
So, the length of the central diagonal is exactly meters and approximately meters.
Answer:

Explanation:
Given the diagonal length, XY, of the end wall of the King’s Chamber of the
Great Pyramid and the length, XZ, of the chamber, find the length, YZ, of the central diagonal is
xy² + xz²  = yz² (using pythagorean theorem)
(7.8)² + (10.5)² = yz²,
yz² = 60.84 +110.25,
yz² = 171.09, square root of 171.09 is 13.08,
yz = 13.08,
So, the length of the cenetral diagonal is exactly 13.08 meters
and approximately 13 meters.

Math in Focus Course 3B Practice 7.3 Answer Key

For this practice, you may use a calculator. Use 3.14 as an approximation for π.
Round your answer to the nearest tenth where necessary.

For each solid, find the value of the variable.

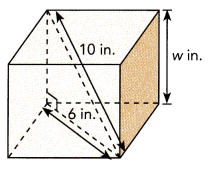
Question 1.

Answer:
The value of variable w is 8 in,

Explanation:
We solid cube have w² + 6 ² = 10² (using pythagorean theorem)
w² = 100 -36,
w² = 64, the value of w is square root of 64 which is 8,
therefore w is 8 in.

Question 2.

Answer:
The value of variable x is 5,

Explanation:
We have x² = 3² + 4² (using pythagorean theorem)
x² = 9 + 16 = 25, the value of x is square root of  25 is 5.

Question 3.

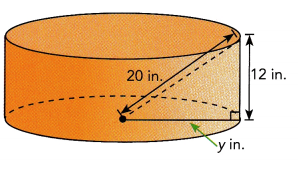
Answer:
The value of variable y is 16 in,

Explanation:
We have 20² = y² + 12² (using pythagorean theorem)
400 = y² + 144,
y² = 400-144 = 256,
so the value of y is sqaure root of 256 is 16,  y = 16 in.

Question 4.

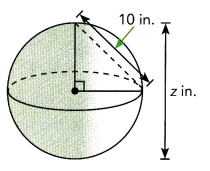
Answer:
The value of variable z is 20 in,

Explanation:
The value of variable z = 2 X 10in = 20 in.

Solve. Show your work. Round your answer to the nearest tenth.

Question 5.
Find the lateral surface area.

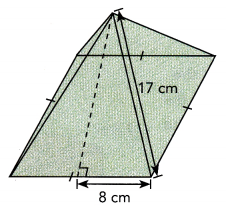
Answer:
The lateral surface area is 272 cm²,

Explanation:
Given square pyramid, the lateral surface area(L.A) is 2bh,
where b is base and h is slant height so L.A = 2 × 8cm × 17 cm = 272 cm².

Question 6.
The area of the lateral surface is πrl, where l is the slant height of the cone.
Find the lateral surface area of the cone.

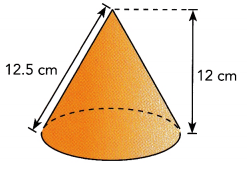
Answer:
The lateral surface of cone is 137.375 cm²,

Explanation:
Given height as 12 cm and slant height l of cone as 12.5 cm so radius of cone is
r ² + 12² = 12.5² (using pythagorean theorem)
r² = 156.25 -144 = 12.25, radius r is square root of 12.25 is 3.5 cm,
now the lateral surface area (L.A) of the cone is  πrl,
L.A = 3.14 × 3.5 × 12.5 = 137.375 cm².

Question 7.
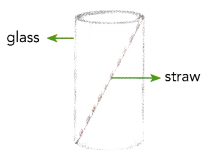
A straw that is 16 centimeters long fits inside the glass shown.
The height of the glass is 14 centimeters. Find the radius of the glass.

Answer:
The radius of the glass is 7.745 approximately 8,

Explanation:
Given a straw that is 16 centimeters long fits inside the glass shown.
The height of the glass is 14 centimeters.
The radius of the glass is 16² = 14² + r² (using pythagorean theorem)
r² = 256- 196 = 60, so r is square root of 60 is 7.745 approximately 8.

Question 8.
A spider sits in a corner of a tank shaped like a rectangular prism. The tank is 13 inches long, 6 inches wide, and 8 inches high. The spider starts to make a web by spinning a length of silk that stretches tightly from one corner along a central diagonal to the opposite corner.

a) Find the length of the diagonal of the rectangular floor of the tank.
Answer:
14.318 is the length of the diagonal of the rectangular floor of the tank,

Explanation:
Given a spider sits in a corner of a tank shaped like a rectangular prism.
The tank is 13 inches long, 6 inches wide, and 8 inches high.
The length of the diagonal of the rectangular floor of the tank is
d² = 13² + 6² = 169 + 36 = 205 so d is square root of 205 is 14.318 in.

b) Find the length of the silk the spider spins from one corner of the tank to the other corner.
Answer:
16.401 in is the length of the silk the spider spins from one corner of the tank to the other corner,

Explanation:
Now the length l of the silk the spider spins from one corner of the tank to the other corner is
l² = 14.318² + 8 ² =  205 + 64 = 269,
so l is square root of 269 is 16.401 in.

Question 9.
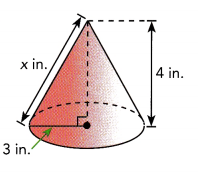
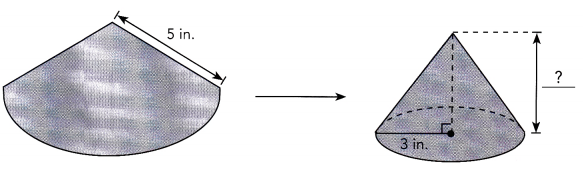
A conical party hat ¡s made from a piece of paper as shown. Given that its radius is 3 inches, find the height of the party hat.

Answer:
The height of the party hat is 4 in,

Explanation:
Given a conical party hat ¡s made from a piece of paper is shown with hypotenues 5 in and  its radius is 3 inches,  let the height of the party hat be h so
5² = 3² + h² (using pythagorean theorem)
h² = 25 – 9 = 16, so h is square root of 16 is 4 in.

Question 10.
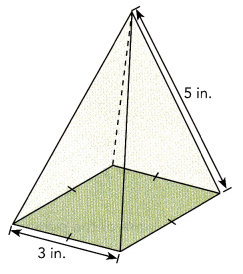
Mindy wants to make a metal paperweight in the shape of a square pyramid. The paperweight will have the dimensions shown.
a) Find the length of a diagonal of the square base.
Answer:

The length of a diagonal of the square base is 4.24 in,

Explanation:
The length of a diagonal of the square base is
l² = 3² + 3² = 9 + 9 = 18,
so the length is square root of 18 is 4.24 in.

b) Find the height of the paperweight.
Answer:
4 in is the height of the paperweight,

Explanation:
Let h be the height of the paperweight so applying
h² + 3² = 5² (using pythagorean theorem),
h² = 25 – 9 = 16, so h is square root of 16 is 4 in.

Question 11.
Math Journal A box shaped like a rectangular prism is 14.5 centimeters long, 4 centimeters wide, and 3.5 centimeters high. You have a ruler that is 15 centimeters long and 3 centimeters wide. Can it fit inside this box? Explain.
Answer:
No, the ruler cannot fit inside the box,

Explanation:
Given a box shaped like a rectangular prism is 14.5 centimeters long,
4 centimeters wide, and 3.5 centimeters high and I have a ruler that is
15 centimeters long and 3 centimeters wide so by seeing the
length of the ruler is 15 cm which is 15-14.5 = 0.5 more than the rectangular prism,
therefore the ruler cannot fit inside the box.