Math in Focus Grade 8 Chapter 1 Lesson 1.4 Answer Key The Power of a Product and the Power of a Quotient

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 1 Lesson 1.4 The Power of a Product and the Power of a Quotient to finish your assignments.

Math in Focus Grade 7 Course 3 A Chapter 1 Lesson 1.4 Answer Key The Power of a Product and the Power of a Quotient

Math in Focus Grade 8 Chapter 1 Lesson 1.4 Guided Practice Answer Key

Simplify each expression. Write your answer in exponential notation.

Question 1.
6³ • 7³
6³ • 7³ = Use the power of a property.
= Simplify.
Answer:
(6 X 7)³ = (42)³,

Explanation:
Given 6³ • 7³  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(6 X 7)³ = (42)³.

Question 2.

Answer:
(5/24)⁴,

Explanation:
Given (-5/6)⁴. (- 1/4)⁴ when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product and quotients of a property,
(-5/6 X -1/4)⁴ = (5/24)⁴.

Question 3.
(1.8)² • (0.75)²
(1.8)² • (0.75)² = Use the power of a property.
= Simplify.
Answer:
((1.8) • (0.75))²,

Explanation:
Given (1.8)² • (0.75)² when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product of a property,
((1.8) • (0.75))².

Simplify each expression. Write your answer in exponential notation.

Question 4.
p⁶ • q⁶
p⁶ • q⁶ = Use the power of a property.
= Simplify.
Answer:
(p X q)⁶ ,

Explanation:
Given p⁶ • q⁶  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(p X q)⁶ .

Question 5.
(3a)⁴ • (4b)⁴
(3a)⁴ • (4b)⁴ = Use the power of a property.
= Simplify.
Answer:
(3a X 4b)⁴ ,

Explanation:
Given (3a)⁴ • (4b)⁴  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property we get (3aX 4b)⁴.

Question 6.
(-3y²)³ • \(\left(\frac{1}{12 y}\right)^{3}\)
Answer:
\(\left(-\frac{y}{4}\right)^{3}\),

Explanation:
Given (-3y²)³ • \(\left(\frac{1}{12 y}\right)^{3}\) on simplification
(-y)^{2 X 3} • \(\left(\frac{1}{4 y}\right)^{3}\) = (-y)^6-3 • \(\left(\frac{1}{4}\right)^{3}\) =
(-y)³ • \(\left(\frac{1}{4}\right)^{3}\) = \(\left(-\frac{y}{4}\right)^{3}\).

Simplify each expression. Write your answer in exponential notation.

Question 7.
2⁵ ÷ 4⁵

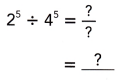
Answer:
\(\left(\frac{1}{2}\right)^{5}\),

Explanation:
Given 2⁵ ÷ 4⁵  as 4 can be written as (2 X 2) so 2⁵ ÷ (2 X 2)⁵ upon simplification
we get 1/2⁵ or \(\left(\frac{1}{2}\right)^{5}\).

Question 8.
(-9)³ ÷ (-3)³

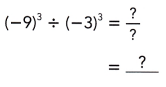
Answer:
(3)³,

Explanation:
Given(-9)³ ÷ (-3)³  as (-9) can be written as (-3 X 3) so (-3 X 3)³ ÷ (-3)³
on simplification we get (3)³.

Simplify each expression. Write your answer in exponential notation.

Question 9.
x⁴ ÷ y⁴

Answer:
\(\left(\frac{x}{y}\right)^{4}\),

Explanation:
Given x⁴ ÷ y⁴ when the variable bases are different and the
powers are the same, the bases are simplified first as (x ÷ y)⁴ and solved.

Question 10.
(8p)⁵ ÷ (3q)⁵
Answer:
(8p ÷ 3q)⁵,

Explanation:
Given (8p)⁵ ÷ (3q)⁵ when the variable bases are different and the
powers are the same, the bases are simplified first as (8p ÷ 3q)⁵ and solved.

Simplify each expression. Write your answer in exponential notation.

Question 11.

Answer:
(2)⁷,

Explanation:

Question 12.

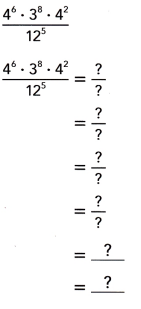
Answer:
(4)³ X (3)³,

Explanation:

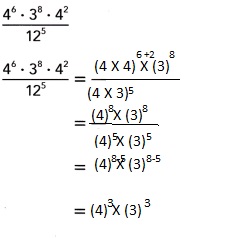
Question 13.

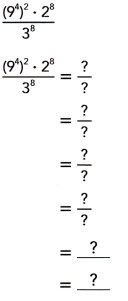
Answer:
(6)⁸,

Explanation:

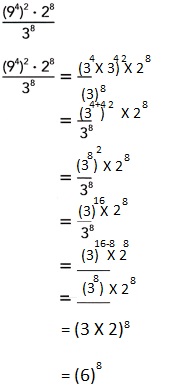
Question 14.
\(\frac{2^{5} \cdot 3^{12} \cdot 2^{7}}{6^{7}}\)
Answer:
(6)⁵,

Explanation:
Given \(\frac{2^{5} \cdot 3^{12} \cdot 2^{7}}{6^{7}}\),
6 can be written as 2 X 3 so \(\frac{2^{5} \cdot 3^{12} \cdot 2^{7}}{({2 X 3})^{7}}\),

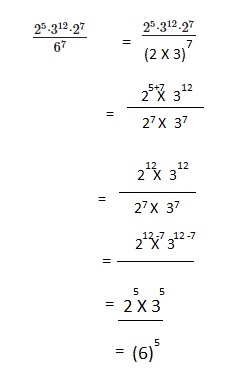
Question 15.
\(\frac{\left(25^{3}\right)^{2} \cdot 7^{6}}{5^{6}}\)
Answer:
(35)⁶,

Explanation:
Given \(\frac{\left(25^{3}\right)^{2} \cdot 7^{6}}{5^{6}}\)

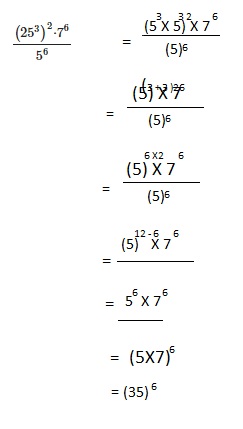
Math in Focus Course 3A Practice 1.4 Answer Key

Simplify each expression. Write your answer in exponential notation.

Question 1.
5⁴ • 6⁴
Answer:
(5 X 6)⁴ = (30)⁴,

Explanation:
Given 5⁴ • 6⁴  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(5 X 6)⁴ = (30)⁴.

Question 2.
5.4³ • 4.5³
Answer:
(5.4 X 4.5)³ = (24.3)³,

Explanation:
Given 5.4³ • 4.5³  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(5.4 X 4.5)³ = (24.3)³.

Question 3.
2⁵ • 10⁵
Answer:
(2 X 10)⁵ = (20)⁵,

Explanation:
Given 2⁵ • 10⁵  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(2 X 10)⁵ = (20)⁵.

Question 4.
a³ • b³
Answer:
(a X b)³ = (ab)³,

Explanation:
Given a³ • b³  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(a X b)³ = (ab)³.

Question 5.
(2x)⁵ • (3y)⁵
Answer:
(2x X 3y)⁵ = (6xy)⁵,

Explanation:
Given (2x)⁵ • (3y)⁵  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(2x X3y)⁵ = (6xy)⁵.

Question 6.
(2.5a)⁶ • (1.6b)⁶
Answer:
(2.5a X 1.6b)⁶ = (4ab)⁶,

Explanation:
Given (2.5a)⁶ • (1.6b)⁶  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(2.5a X 1.6b)⁶ = (4ab)⁶.

Question 7.
\(\left(-\frac{1}{3}\right)^{4} \cdot\left(-\frac{2}{5}\right)^{4}\)
Answer:
\(\left(\frac{2}{15}\right)^{4}\),

Explanation:
Given \(\left(-\frac{1}{3}\right)^{4} \cdot\left(-\frac{2}{5}\right)^{4}\)
when the variable bases are different and the powers are the same,
the bases are multiplied first,Used the powers of product property,
\(\left(\frac{-1 X -2}{3X 5}\right)^{4}\) = \(\left(\frac{2}{15}\right)^{4}\).

Question 8.
9² ÷ 3²
Answer:
(3)²,

Explanation:
Given (9)² ÷ (3)²  as 9 = 3 X 3 can be written as (3²)² so (3)⁴ ÷ (3)²
on simplification we get (3)^4-2 = (3)².

Question 9.
10⁶ ÷ 5⁶
Answer:
(2)⁶,

Explanation:
Given (10)⁶ ÷ (5)⁶  as 10 can be written as (5 x 2)⁶ so (5)⁶ .(2)⁶ ÷ (5)⁶
on simplification we get (2)⁶.

Question 10.
2.8⁷ ÷ 0.7⁷
Answer:
(4)⁷,

Explanation:
Given (2.8)⁷ ÷ (0.7)⁷  as 2.8 ÷ 0.7 = 4 so can be written as (4)⁷ .

Question 11.
15² ÷ 25²
Answer:
\(\left(\frac{3}{5}\right)^{2}\),

Explanation:
Given 15² ÷ 25², 15² can be written as (5 X 3)² and 25²  as (5 X 5)²  ,
upon simplification we get \(\left(\frac{3}{5}\right)^{2}\).

Question 12.
7.2⁹ ÷ 2.4⁹
Answer:
(3)⁹,

Explanation:
Given (7.2)⁹ ÷ (2.4)⁹  as 7.2 ÷ 2.4 = 3, so can be written as (3)⁹.

Question 13.
(3.2x)⁹ ÷ (1.1y)⁹
Answer:
(3.2x ÷ 1.1y)⁹,

Explanation:
Given (3.2x)⁹ ÷ (1.1y)⁹ when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property (3.2x ÷ 1.1y)⁹.

Question 14.
(-6)⁸ ÷ (-2)⁸
Answer:
(3)⁸,

Explanation:
Given (-6)⁸ ÷ (-2)⁸  as -6 can be written as (-2 x 3)⁸ so (-2)⁸ .(3)⁸ ÷ (-2)⁸
on simplification we get (3)⁸.

Question 15.
s⁵ ÷ r⁵
Answer:
\(\left(\frac{s}{r}\right)^{5}\),

Explanation:
Given s⁵ ÷ r⁵ the variable bases are different and the
powers are the same, the bases are divided first,upon simplification we get
\(\left(\frac{s}{r}\right)^{5}\).

Question 16.
(3a)⁶ ÷ (2b)⁶
Answer:
\(\left(\frac{3a}{2b}\right)^{6}\),

Explanation:
Given (3a)⁶ ÷ (2b)⁶ the variable bases are different and the
powers are the same, the bases are divided first, upon simplification we get
\(\left(\frac{3a}{2b}\right)^{6}\).

Question 17.
(h²k⁵)⁴
Answer:
h⁸k²⁰,

Explanation:
Given (h²k⁵)⁴ when the variable bases are different and the
powers are the same,Used the powers of product and
quotients of a property we get h^{2X 4} X k^5X4 = h⁸k²⁰.

Question 18.
\(\left(\frac{32 m^{6}}{4 n^{4}}\right)^{2}\)
Answer:
\(\left(\frac{8 m^{6}}{4n^{4}}\right)^{2}\),

Explanation:
Given \(\left(\frac{32 m^{6}}{4 n^{4}}\right)^{2}\) upon simplification
we get \(\left(\frac{8 m^{6}}{4n^{4}}\right)^{2}\).

Question 19.
\(\frac{9^{2} \cdot 9^{7}}{3^{5} \cdot 3^{4}}\)
Answer:
(3)⁹,

Explanation:
Given \(\frac{9^{2} \cdot 9^{7}}{3^{5} \cdot 3^{4}}\)
9 can be written as \(\frac{3 X 3 ^{2} \cdot 3 X 3^{7}}{3^{5} \cdot 3^{4}}\)
when bases are same powers are added \(\frac{3^{2+2+7+7}}{3^{5+4}}\) =
\(\frac{3^{18}}{3^{9}}\) on further simplification we get (3)^18-9 = (3)^9.

Question 20.
\(\frac{6^{5} \cdot 2^{3} \cdot 6^{4}}{12^{3}}\)
Answer:
(6)⁶,

Explanation:
Given\(\frac{6^{5} \cdot 2^{3} \cdot 6^{4}}{12^{3}}\) upon simplification
\(\frac{6^{5+4} \cdot 2^{3} }{6 X 2^{3}}\) = \(\frac{6^{9} \cdot 2^{3} }{(6 X 2)^{3}}\)=
(6)^9-3 = (6)⁶.

Question 21.
\(\frac{\left(5^{4}\right)^{2} \cdot 6^{8}}{10^{8}}\)
Answer:
(3)⁸,

Explanation:
Given \(\frac{\left(5^{4}\right)^{2} \cdot 6^{8}}{10^{8}}\) as denominator
10 can be written as 5 X 2 so \(\frac{\left(5\right)^{8} \cdot 6^{8}}{(5 X 2)^{8}}\) we get
\(\frac{6^{8}}{2^{8}}\) = \(\frac{(2 X 3)^{8}}{2^{8}}\) = (3)⁸.

Question 22.
\(\frac{\left(6^{3}\right)^{3} \cdot 4^{9}}{8^{9}}\)
Answer:
(3)⁹,

Explanation:
Given \(\frac{\left(6^{3}\right)^{3} \cdot 4^{9}}{8^{9}}\) as denominator
8 can be written as 4 X 2 so  we get
\(\frac{\left((2 X 3)^{3}\right)^{3} \cdot 4^{9}}{(4 X 2)^{9}}\) = (3)⁹.

Question 23.
\(\frac{24^{9}}{4^{3} \cdot 6^{2} \cdot 4^{6}}\)
Answer:
(6)⁷,

Explanation:
Given \(\frac{24^{9}}{4^{3} \cdot 6^{2} \cdot 4^{6}}\) as
24 in numerator can be written as 4 X 6 so

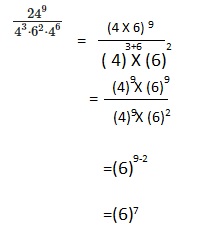
Question 24.
\(\frac{9^{12}}{\left(3^{3}\right)^{3} \cdot 3^{3}}\)
Answer:
(3)¹²,

Explanation:

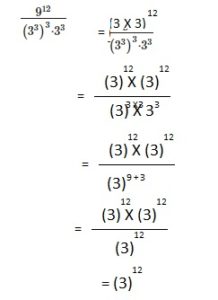
Question 25.
Math Joural Charles thinks that a³ • b³ = ab⁶. Is he correct? Why?
Answer:
No, Charles is incorrect,

Explanation:
a³ • b³ ≠ ab⁶ it should be (ab)³ as when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property we get (aX b)³ ≠ ab⁶.

Solve. Show your work.

Question 26.
At the beginning of January, Mr. Howard gives his niece $1 to start a savings account.
For each month that she can triple the amount in the account,
Mr. Howard will double the amount in the account at the end of each month.
How much does Mr. Howard’s niece have in her account at the beginning of May?
Answer:
$7,776 Mr. Howard’s niece have in her account at the beginning of May,

Explanation:
Given at the beginning of January, Mr. Howard gives his niece $1 to start a savings account.
For each month that she can triple the amount in the account,
Mr. Howard will double the amount in the account at the end of each month.
So at the beginning of January it is

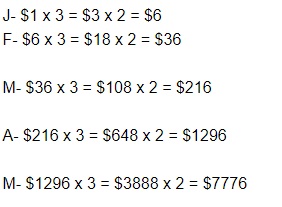
therefore,$7,776 Mr. Howard’s niece have in her account at the beginning of May.