Math in Focus Grade 8 Chapter 1 Lesson 1.6 Answer Key Real-World Problems: Squares and Cubes

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 1 Lesson 1.6 Real-World Problems: Squares and Cubes to finish your assignments.

Math in Focus Grade 7 Course 3 A Chapter 1 Lesson 1.6 Answer Key Real-World Problems: Squares and Cubes

Math in Focus Grade 8 Chapter 1 Lesson 1.6 Guided Practice Answer Key

Solve. Show your work.

Question 1.
Find the two square roots of 169.

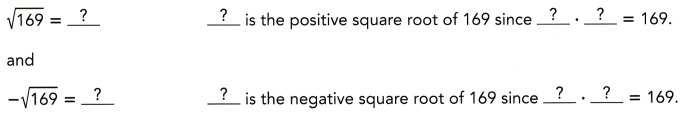
Answer:
Explanation:
Given to find two square roots of 169 and -169,So using prime factorization
we get for 169 it is 13 and for – 169 it is -13

Solve. Show your work.

Question 2.
Find the cube root of \(\frac{1}{729}\).

Answer:
1/9,

Explanation:

Solve. Show your work.

Question 3.
x² = 2.25
x² = 2.25

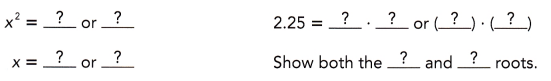
Answer:
1.5,

Explanation:

Solve. Show your work.

Question 4.

Answer:
x = (1/2),

Explanation:

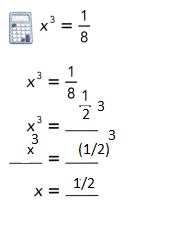
Question 5.
A square field has an area of 98.01 square meters. Find the length of each side of the field.
Let the length of each side be x meters.
x² = Translate into an equation.
= Solve for x by taking the positive root of both sides.
x = m Use a calculator to find the square root.
The length of each side is meters.
Answer:
x² = 98.01 We translate into an equation:
\(\sqrt{x^{2}}\) = \(\sqrt{98.01}\) We solve for x by taking the positive square root of both sides:
x = 9.9m We use a calculator to find the square root:
The length of each side is 9.9 meters.
9.9 meters

Solve. Show your work.

Question 6.
Robin bought a crystal globe that has a volume of 1,774\(\frac{2}{3} \pi\)ir cubic centimeters. Find the radius of the crystal globe.
Let the radius of the crystal globe be r centimeters.

Answer:
The radius of the crystal globe is 29.7 cms,

Explanation:

Question 7.
A spherical waterme’on has a volume of 562.5π cubic centimeters. What is the diameter of the watermelon?

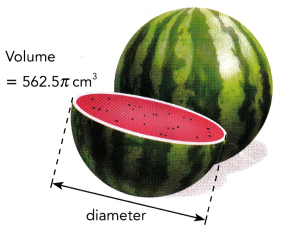
Let the radius of the watermelon be r centimeters.

Answer:
The diameter of the watermelon is 15 centimeters,

Explanation:

Math in Focus Course 3A Practice 1.6 Answer Key

Find the two square roots of each number. Round your answer to the nearest tenth when you can.

Question 1.
25
Answer:
5, or -5,

Explanation:
Given to find sqaure roots of 25
1. 5 X 5 = 25,
2. -5 X -5 = 25,
so 5, or -5.

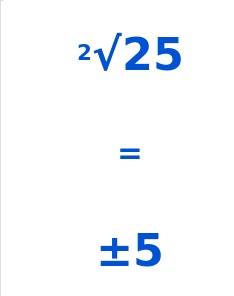
Question 2.
64
Answer:
8 or -8,

Explanation:
Given to find sqaure roots of 64
1. 8 X 8 = 64,
2. -8 X -8 = 64,
so 8, or -8.

Question 3.
80
Answer:
8.944 or -8.944,

Explanation:
Given to find sqaure roots of 64
1. 8.944 X 8.944 = 80,
2. -8.944 X -8.944 = 80,
so 8.944, or -8.944.

Question 4.
120
Answer:
10.9544 or -10.9544,

Explanation:
Given to find sqaure roots of 64
1. 10.9554 X 10.9554 = 120,
2. -10.9554X -10.9554 = 120,
so 10.9554, or -10.5994.

Find the cube root of each number. Round your answer to the nearest tenth when you can.

Question 5.
512
Answer:
8

Explanation:

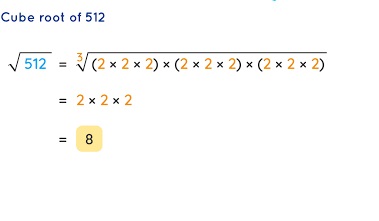
Question 6.
1,000
Answer:
10

Explanation:

Question 7.
999
Answer:
9.997,

Explanation:

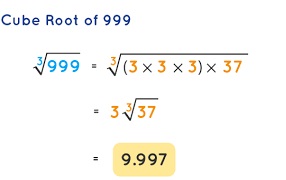
Question 8.
\(\frac{64}{343}\)
Answer:
\(\frac{4}{7}\),

Explanation:
As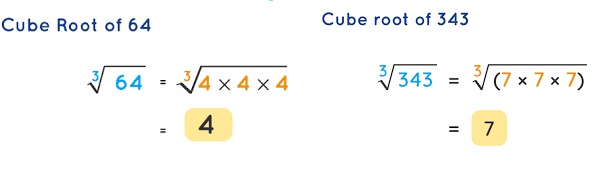

 

 

So Cube root of \(\frac{64}{343}\) is \(\frac{4}{7}\).

Solve each equation involving a variable that ¡s squared.
Round your answer to the nearest tenth when you can.

Question 9.
a² = 46.24
Answer:
a= 6.8,

Explanation:

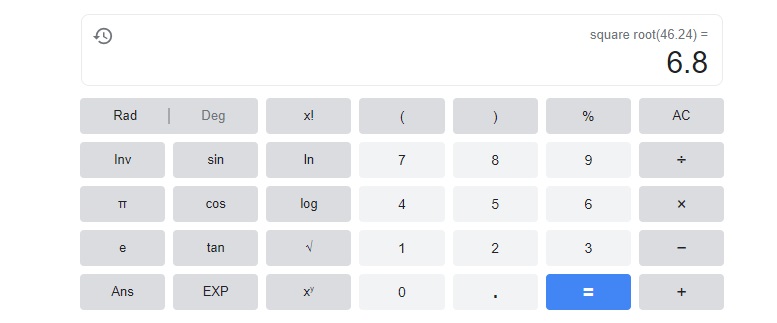
Question 10.
b² = \(\frac{25}{49}\)
Answer:
b= \(\frac{5}{7}\),

Explanation:
Given b² = \(\frac{25}{49}\) as b² = \(\frac{5X5}{7X7}\),
therefore b = square root of \(\frac{5X 5}{7 X 7}\) = \(\frac{5}{7}\),

Question 11.
m² = 196
Answer:
m = 14,

Explanation:

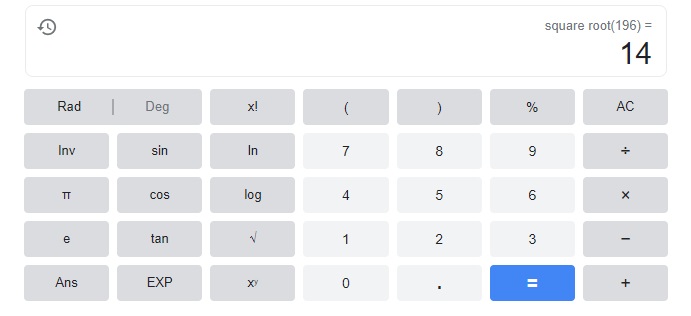
Therefore m = 14.

Question 12.
n² = 35o
Answer:
n= 18.708,

Explanation:

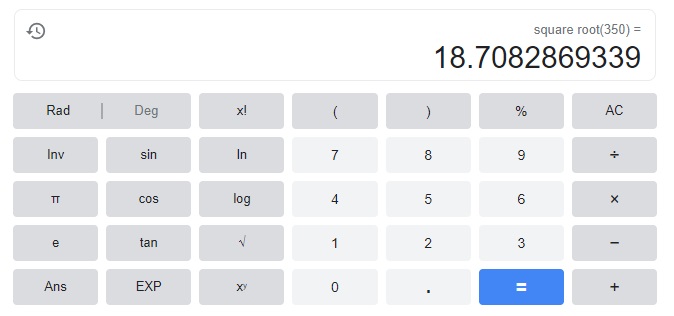
therefore n = 18.708.

Solve each equation involving a variable that is cubed.
Write fractions in simplest form, and round decimal answers
to the nearest tenth.

Question 13.
x³ = 74.088
Answer:
x =4.2,

Explanation:

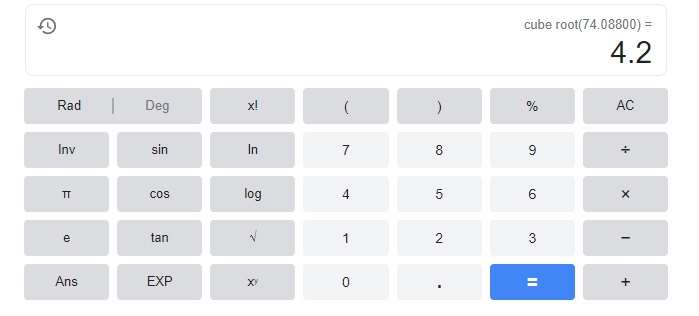
the cube root of 74.088 is 4.2.

Question 14.
x³ = \(\frac{216}{729}\)
Answer:
x = \(\frac{6}{9}\),

Explanation:

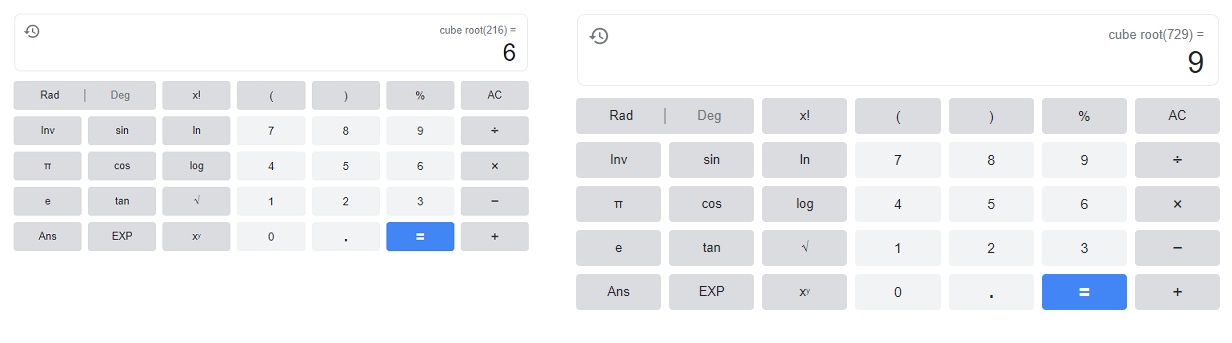
the cube root of x³ = \(\frac{216}{729}\) so x = \(\frac{6}{9}\).

Question 15.
x³ = 1,728
Answer:
x= 12,

Explanation:

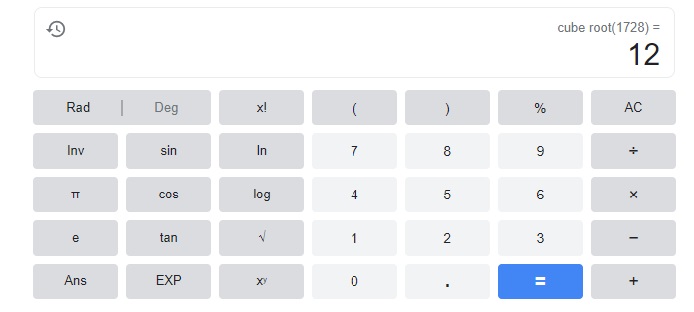
Question 16.
x³ = 2,500
Answer:
x= 13.572,

Explanation:

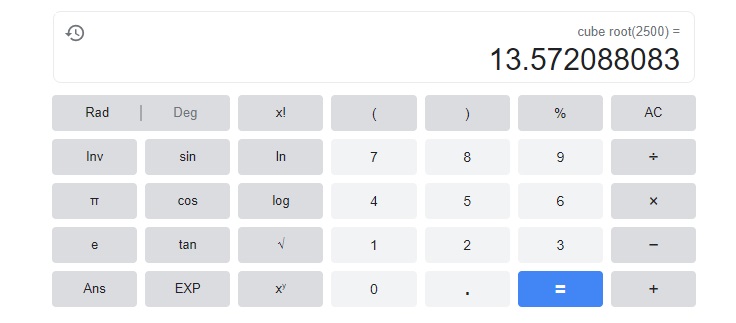
the cube root x = 13.572088083.

Solve. Show your work. Round to the nearest tenth.

Question 17.
The volume of a spherical tank is 790.272π cubic feet.
What is the diameter of the container?

Answer:
The diameter of the container is 16.8 ft,

Explanation:
Given the volume of a spherical tank is 790.272π cubic feet.
so radius is 4/3 pi r³ = 790.272π,
r³ = (790.272 X 3)/4 = 592.704,
r= 8.4,

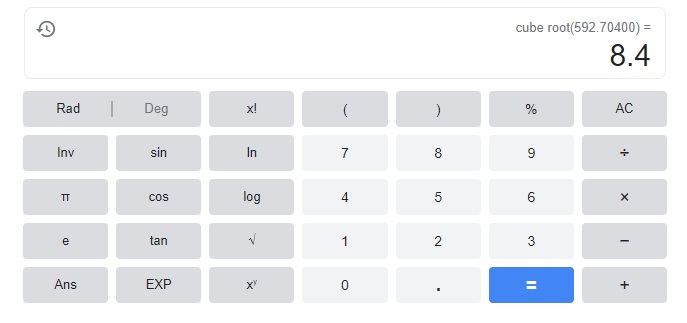
diameter of the container is 2r = 2 X 8.4 = 16.8 ft.

Question 18.
An orchard planted on a square plot of land has 3,136 apple trees.
If each tree requires an area of 4 square meters to grow,
find the length of each side of the plot of land.

Answer:
The length of each side of plot is 112 meters,

Explanation:
Given an orchard planted on a square plot of land has 3,136 apple trees.
If each tree requires an area of 4 square meters to grow,
the length of each side of the plot of land of square root of 3136 X 4
sqaure root of 12544 = 112 meters.

Question 19.
Mr. Berman deposited $2,500 in a savings account. Three years later there
was $2,812.16 in the savings account. Use the formula A = P(1 + r)ⁿ to find
the rate of interest, r percent, that he was paid. A represents the final amount of the
investment, P is the original principal, and n is the number of years it was invested.
Answer:
Rate of intreset is 5.78%,

Explanation:
Given Mr. Berman deposited $2,500 in a savings account. Three years later there
was $2,812.16 in the savings account. Using the formula A = P(1 + r)ⁿ to find
the rate of interest, r percent, that he was paid. A represents the final amount of the
investment, P is the original principal, and n is the number of years it was invested,
$2812.16 = $2,500(1 + r)³
$2812.16 – $2,500 = (1 + r)³
(1 + r)³ = $312.16
1 + r = cube root of $312.16,

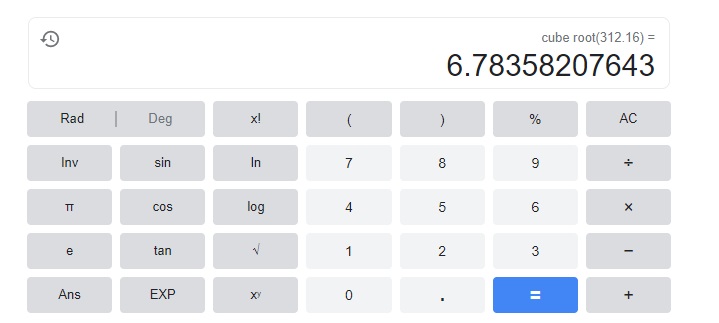
1 + r = 6.7835,
therefore r = 6.7835 – 1 = 5.7835.

Brain @ Work

Question 1.
Evaluate \(\frac{4^{3} \cdot 10^{4}}{5^{2}}\) without using a calculator.
Answer:
2¹⁰ X 5²,

Explanation:

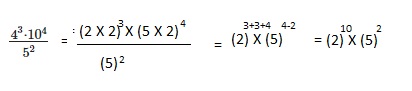
Question 2.
Find the values of x and y that make the equation \(\frac{81 x^{4} \cdot 16 y^{4}}{\left[(2 y)^{2}\right]^{2}}\) = 1,296 true,
Answer:
X = 1.414 and y = 1,

Explanation:

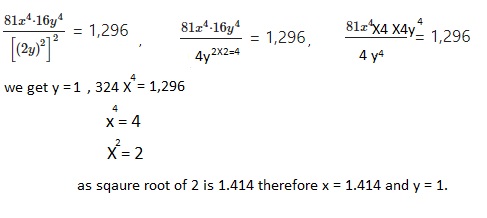
Question 3.
Use each of the numbers 1 to 9 exactly once to fill in the blanks.

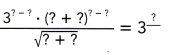
Answer:
3¹¹,

Explanation:
Used each of the numbers 1 to 9 exactly once to fill the blanks

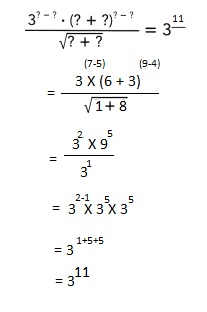
Question 4.
Jeremy wants to measure the radius of a marble. He uses a tank and
filled the tank with 360 identical marbles shown below, If the volume of the
tank is 9,720 cubic inches, find the radius of each marble.

Answer:
Radius is 3 inches,

Explanation:
Given Jeremy wants to measure the radius of a marble. He uses a tank and
filled the tank with 360 identical marbles shown below, If the volume of the
tank is 9,720 cubic inches, volume of each cube is 9,720 ÷ 360 = 27,
radius is cube root of 27 = 3 inches.