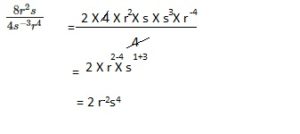Math in Focus Grade 8 Chapter 1 Lesson 1.5 Answer Key Zero and Negative Exponents

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 1 Lesson 1.5 Zero and Negative Exponents to finish your assignments.

Math in Focus Grade 7 Course 3 A Chapter 1 Lesson 1.5 Answer Key Zero and Negative Exponents

Math in Focus Grade 8 Chapter 1 Lesson 1.5 Guided Practice Answer Key

Hands-On Activity

Understand the zero exponent

Work individually.

Step 1.
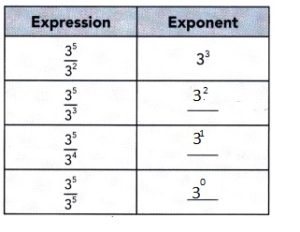
Use the power of a quotient property to simplify each expression. Write the quotient as an exponent.

Step 2.
In factored form, the quotient \(\frac{3^{5}}{3^{5}}\) is \(\frac{3 \cdot 3 \cdot 3 \cdot 3 \cdot 3}{3 \cdot 3 \cdot 3 \cdot 3 \cdot 3}\). If you divide out all the common factors in the numerator and denominator, what is the value of \(\frac{3^{5}}{3^{5}}\)?

Step 3.
Based on your findings, what can you conclude about the value of 3°?

Step 4.
Make a prediction about the value of any nonzero number raised to the zero power. Then, use a calculator to check your prediction for several numbers. For example, to raise the number —2 to the zero power, you can enter these keystrokes:

Does your prediction hold true?
Answer:
Step 1:

Wrote the quotient as an exponent of 3° used exponent \(\frac{3^{5}}{3^{5}}\),
Step 2:
Value is 1,
Step 3:
The value of 3° is 1.
Step 4:
Yes,

Explanation:
Step 1:
Used the power of a quotient property to simplify each expression.
Wrote the quotient as an exponent of 3° used exponent \(\frac{3^{5}}{3^{5}}\),
Step2:
In factored form, the quotient \(\frac{3^{5}}{3^{5}}\) is \(\frac{3 \cdot 3 \cdot 3 \cdot 3 \cdot 3}{3 \cdot 3 \cdot 3 \cdot 3 \cdot 3}\). If you divide out all the common factors in the numerator and denominator the value of \(\frac{3^{5}}{3^{5}}\) is 1 ,
Step 3 :
Any number to power 0 the value is 1, so the value of 3° is 1,
Step 4:
Makeing a prediction about the value of any nonzero number raised to the zero power.
Then, using a calculator to check your prediction for several numbers.
For example, to raise the number —2 to the zero power, you can enter these keystrokes:

Yes my predictions hold true as
Any number to power 0 the value is 1.

Simplify each expression and evaluate where applicable.

Question 1.

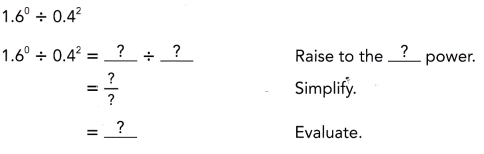
Answer:
(0.4)^-2,

Explanation:

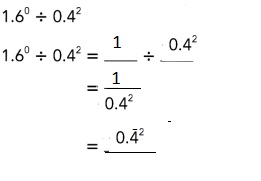
Question 2.

Answer:
1,

Explanation:

Question 3.
\(\frac{t^{0} \cdot t^{7}}{t^{5}}\)
Alternatively, you can also apply the product of powers property to the expression t° ∙ t⁷ to get t⁰⁺⁷ = t⁷.
Answer:
t²,

Explanation:
Given\(\frac{t^{0} \cdot t^{7}}{t^{5}}\) as t⁰ is equal to 1  so
we get 1 X t^7-5= t².

Hands-On Activity

Work individually.

Step 1.
Use the quotient of powers property to simplify each expression. Write the quotient in exponential notation.

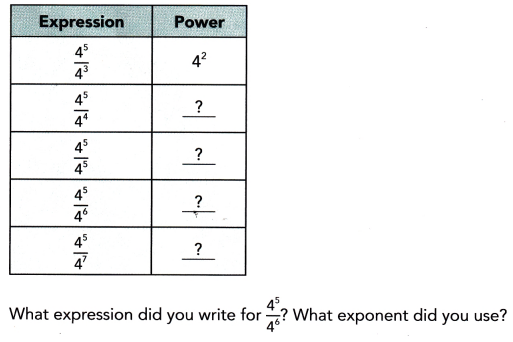
Answer:

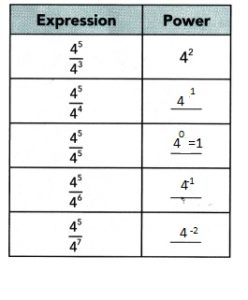
Explanation:
Wrote the quotient in exponential notation above,
As (4)⁵÷ (4)⁶ = (4)^5-6= (4)^-1 used negative exponent.

Step 2.
In factored form, the quotient \(\frac{4^{5}}{4^{6}}\) is \(\frac{4 \cdot 4 \cdot 4 \cdot 4 \cdot 4}{4 \cdot 4 \cdot 4 \cdot 4 \cdot 4 \cdot 4}\). If you divide out all the common factors in the numerator and denominator, what is the value of
\(\frac{4^{5}}{4^{6}}\)?

Answer:
The value is (4)^-1,

Explanantion:
(4)⁵÷ (4)⁶ = (4)^5-6= (4)^-1 used negative exponent.

Step 3.
Repeat Step 2 for \(\frac{4^{5}}{4^{7}}\). What is the value of \(\frac{4^{5}}{4^{7}}\)?

Answer:
The value is (4)^-2,

Explanantion:
(4)⁵÷ (4)⁷ = (4)^5-7= (4)^-2.

Math Journal
Suppose a represents any nonzero number. How would you write a^-3 using a positive exponent?

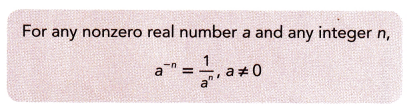
Simplify each expression and evaluate where applicable.
Answer:
1 ÷ a³ ,

Explanation:
Given  a^-3 using a positive exponent for any nonzero real
number a and any integer 3, a^-3 = 1 ÷ a³ ,a ≠ 0.

Question 4.

Answer:
(2.5)^-3,

Explanantion:

Question 5.

Answer:
(-6)^-1,

Explanation:

Simplify each expression. Write your answer using a positive exponent.

Question 6.
14a^-5 ÷ (7a • 2a^-4)
14a^-5 ÷ (7a • 2a^-4) = Write the expression as a .
=
Answer:
1,

Explanation:

Usually you should write your answer using a positive exponent
unless asked to use a negative exponent.

Math in Focus Course 3A Practice 1.5 Answer Key

Simplify each expression and evaluate.

Question 1.
8³ • 8°
Answer:
8³,

Explanation:
Given 8³ • 8° any number to power 0 the value is 1, so the value of 8° is 1,
so 8³ • 8° = 8³ • 1 = 8³.

Question 2.
5⁴ • (-5)°
Answer:
5⁴,

Explanation:
Given 5⁴ • (-5)° any number to power 0 the value is 1, so the value of (-5)° is 1,
so 5⁴ • (-5)° = 5⁴ • 1 = 5⁴.

Question 3.
\(\left(\frac{1}{3}\right)^{4} \cdot\left(\frac{1}{3}\right)^{0}\)
Answer:
\(\left(\frac{1}{3}\right)^{4}\),

Explanation:
Given \(\left(\frac{1}{3}\right)^{4} \cdot\left(\frac{1}{3}\right)^{0}\) as
\(\left(\frac{1}{3}\right)^{0}\) = 1 therefore \(\left(\frac{1}{3}\right)^{4}\) X 1 =
\(\left(\frac{1}{3}\right)^{4}\).

Question 4.
7 • 10³ + 4² • 10² + 5 • 10°
Answer:
8,605,

Explanation:
Given 7 • 10³ + 4² • 10² + 5 • 10° solving as 7 X 10 X 10 X 10 + 4 X 4 X 10 X 10 + 5 X 1 =
7 X 1,000 + 16 X 100 + 5 = 7,000 + 1,600 + 5 = 8,605.

Question 5.
(2.3) • 10² + 5 • 10¹ + 1 • 10°
Answer:
281,

Explanation:
Given (2.3) • 10² + 5 • 10¹ + 1 • 10° solving as (2.3) X 10 X 10 + 5 X 10 + 1 X 1 =
230 + 50 + 1 =281.

Question 6.
\(\frac{7^{4} \cdot 7^{5}}{7^{9}}\)
Answer:
1,

Explanation:
Given \(\frac{7^{4} \cdot 7^{5}}{7^{9}}\) solving
\(\frac{7^{4+5}}{7^{9}}\) = \(\frac{7^{9}}{7^{9}}\)=
(7)^9-9 =(7)⁰ = 1.

Question 7.
(9^-3)° • 5²
Answer:
5²,

Explanation:
Given (9^-3)° • 5² any number to power 0 the value is 1,
so the value of (9^-3)°  is 1, therefore 1 X 5² = 5².

Question 8.
\(\frac{\left(6^{-3}\right)^{-2} \cdot 8^{6}}{48^{6}}\)
Answer:
1

Explanation:

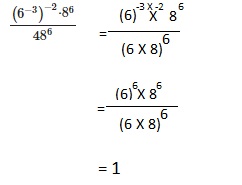
Simplify each expression. Write your answer using a negative exponent.

Question 9.
7³ • 7^-4
Answer:
7^-1,

Explanation:
Given 7³ • 7^-4  using products of powers property we get
7^3-4 = 7^-1.

Question 10.
\(\frac{(-5)^{-2}}{(-5)^{3}}\)
Answer:
\(\frac{(-5)^{-2}}{(-5)^{3}}\) simplify
= (-5)^-1

Question 11.

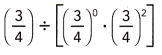
Answer:

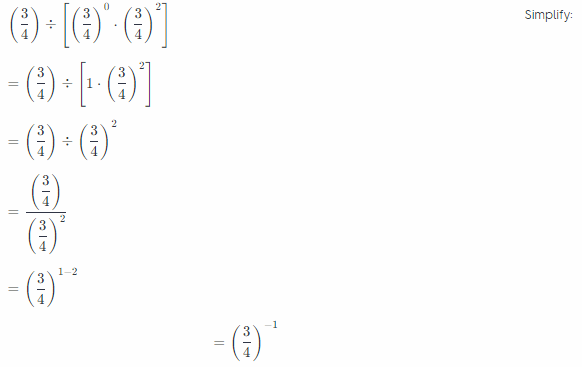
Question 12.
\(\left(\frac{2}{5}\right)^{-4} \cdot\left(\frac{2}{5}\right)^{-1} \div\left(\frac{2}{5}\right)^{-3}\)
Answer:
\(\left(\frac{2}{5}\right)^{-2}\),

Explanation:

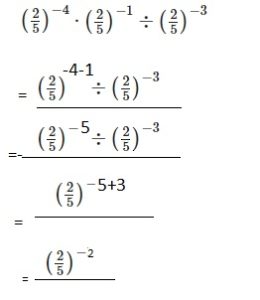
Question 13.
\(\frac{x^{0}}{x^{2} \cdot x^{3}}\)
Answer:
x ^-5,

Explanation:

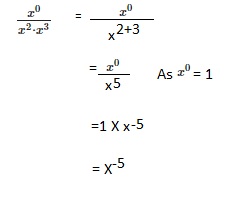
Question 14.
\(\frac{4 h^{-5} \cdot 6 h^{-2}}{3 h^{-3}}\)
Answer:
8(h)^-4,

Explanation:

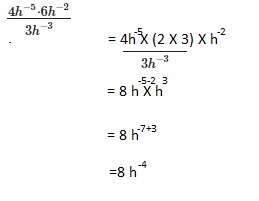
Simplify each expression. Write your answer ustng a positive exponent.

Question 15.
1.2° ÷ 1.8²
Answer:
0.308,

Explanation:
Given 1.2° ÷ 1.8² any number to power 0 the value is 1,
so the value of (1.2)° is 1, therefore 1÷1.8² = 1 ÷ 3.24 = 0.308.

Question 16.
5.2^-3 ÷ 2.6^-3
Answer:
0.125,

Explanation:
Given 5.2^-3 ÷ 2.6^-3  we get  2.6³ ÷ 5.2³ upon solving
(2.6 X 2.6 X 2.6) ÷ (5.2 X 5.2 X 5.2) = 0.125.

Question 17.
\(\frac{(-3)^{-4}}{(-3)^{2}}\)
Answer:
\(\frac{(1)}{(-3)^{6}}\),

Explanation:
Given

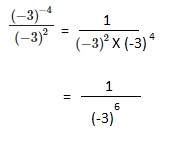
Question 18.
\(\left(\frac{5}{6}\right)^{-4} \cdot\left(\frac{5}{6}\right)^{-2} \div\left(\frac{5}{6}\right)^{-3}\)
Answer:
\(\frac{(1)}{\frac{5}{6}^{3}}\),

Explanation:

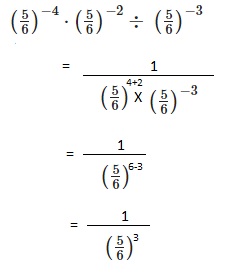
Question 19.
\(\frac{9 k^{-1} \cdot 2 k^{-3}}{27 k^{-6}}\)
Answer:
2k² ÷ 3,

Explanation:

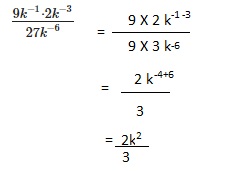
Question 20.
\(\frac{c^{-4} \cdot c^{12}}{c^{-7}}\)
Answer:
(c)¹⁵,

Explanation:

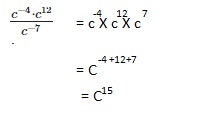
Evaluate each numeric expression.

Question 21.
\(\frac{7^{-2} \cdot 7^{0}}{8^{3} \cdot 8^{-5}}\)
Answer:
(8/7)²,

Explanation:

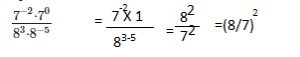
Question 22.
\(\frac{\left(7^{-2}\right)^{2} \cdot 9^{-4}}{21^{-4}}\)
Answer:
(3)^-4,

Explanation:

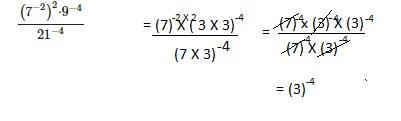
Question 23.
\(\frac{10^{0}}{2^{-2} \cdot\left(5^{-1}\right)^{2}}\)
Answer:
100,

Explanation:

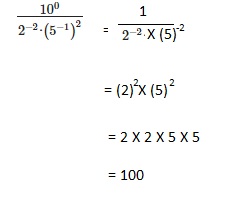
Question 24.
\(\frac{\left(3^{6}\right)^{-2}}{6^{-9}\left(-2^{10}\right)}\)
Answer:
(-1/54),

Explanation:

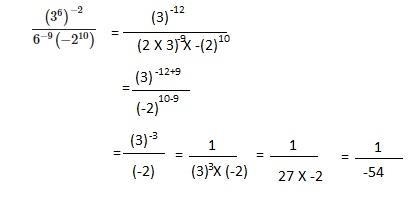
Simplify each algebraic expression.

Question 25.
\(\left(\frac{7 m^{3}}{-49 n^{0}}\right)^{-1}\)
Answer:
(-7)m^-3,

Explanation:

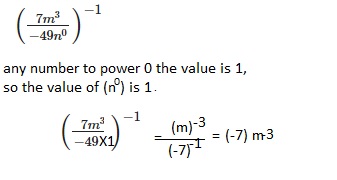
Question 26.
\(\frac{8 r^{2} s}{4 s^{-3} r^{4}}\)
Answer:
2r^-2s⁴,

Explanation: