Math in Focus Grade 8 Chapter 1 Review Test Answer Key

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 1 Review Test to finish your assignments.

Math in Focus Grade 8 Course 3 A Chapter 1 Review Test Answer Key

Concepts and Skills

Identify the base and exponent in each expression.

Question 1.
\(\left(-\frac{1}{5}\right)^{-3}\)
Answer:
base is \(\left(-\frac{1}{5}\right)\) and exponent is -3,

Explanation:
Given \(\left(-\frac{1}{5}\right)^{-3}\) so base is
base value is \(\left(-\frac{1}{5}\right)\) and exponent value is -3,

Question 2.
-0.92⁴
Answer:
base is (-0.92) and exponent is 4,

Explanation:
Given -0.92⁴ here the base is -0.92 and exponent is 4.

Tell whether each statement is correct. If it is incorrect, state the reason.

Question 3.
-0.7³ = -0.7 • 0.7 • 0.7
Answer:
Statement is incorrect,

Explanation:
Given -0.7³ = -0.7 • 0.7 • 0.7 which is incorrect the correct statement is
-0.7³ = -0.7 • -0.7 • -0.7.

Question 4.
5^-4 = (-5) • (-5) • (-5) • (-5)
Answer:
Statement is correct,

Explanation:
Given statement is
5^-4 = (-5) • (-5) • (-5) • (-5) is correct.

Write in exponential notation.

Question 5.
2 • 2 • 2 • 2
Answer:
2⁴,

Explanation:
Given 2 • 2 • 2 • 2 here base is 2 and exponent is 4 therefore
the exponential notation is 2⁴.

Question 6.
4.8 • 4.8
Answer:
4.8²,

Explanation:
Given 4.8 • 4.8 here base is 4.8 and exponent is 2 therefore
the exponential notation is 4.8².

Question 7.
\(\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2}\)
Answer:
\(\frac{1}{2}\),

Explanation:
Given \(\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2}\) here base is \(\frac{1}{2}\) and exponent is 3 therefore the exponential notation is \(\left(\frac{1}{2}\right)^{3}\).

Question 8.
c • c • c • c • c • c
Answer:
c⁶,

Explanation:
Given c • c • c • c • c • c here base is c and exponent is 6 therefore
the exponential notation is c⁶.

Question 9.
\(\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2}\)
Answer:
\(\frac{1}{2}\),

Explanation:
Given \(\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2}\) here base is \(\frac{1}{2}\) and exponent is 3 therefore the exponential notation is \(\left(\frac{1}{2}\right)^{3}\).

Question 10.
(-1.2)(-1.2)(-1.2)(-1.2)
Answer:
(-1.2)⁴,

Explanation:
Given (-1.2)(-1.2)(-1.2)(-1.2)  here base is (-1.2) and exponent is 4 therefore
the exponential notation is (-1.2)⁴.

Write the prime factorization of each number in exponential notation.

Question 11.
3,780
Answer:
Prime factorization of 3,780 = 2² X 3³ X 5 X 7,

Explanation:

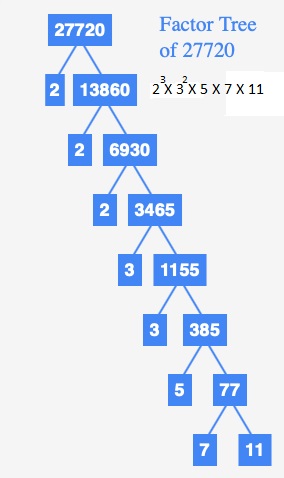
Question 12.
27,720
Answer:
Prime factorization of 27,720 = 2³ X 3² X 5 X 7 X 11,

Explanation:

Expand and evaluate each expressions.

Question 13.
(-6)²
Answer:
36,

Explanation:
Given (-6)² so upon expanding we get (-6) X (-6) = 36.

Question 14.
1.1²
Answer:
1.21,

Explanation:
Given (1.1)² so upon expanding we get (1.1) X (1.1) = 1.21.

Question 15.
10⁵
Answer:
100,000

Explanation:
Given 10⁵ so upon expanding we get 10 X 10 X 10 X 10 X 10 = 100,000.

Question 16.
\(\left(\frac{2}{3}\right)^{3}\)
Answer:
\((\frac{8}{27}\),

Explanation:
Given\(\left (\frac{2}{3}\right)^{3}\) so upon expanding we get
\((\frac{2}{3})\) X \((\frac{2}{3})\) X \((\frac{2}{3})\) =
\((\frac{2X 2 X 2}{3 X 3 X 3})\) = \((\frac{8}{27})\).

Simplify each expression. Write your answer using a positive exponent.

Question 17.
(-3)^-1 . (-3)°
Answer:
\(\frac{1}{-3}\),

Explanation:
Given (-3)^-1 . (-3)° as (-3)°  is 1 and (-3)^-1 value in positive exponent is
\(\frac{1}{-3}\).

Question 18.
\(\left(\frac{5}{6}\right)^{4} \cdot\left(\frac{5}{6}\right)^{3}\)
Answer:

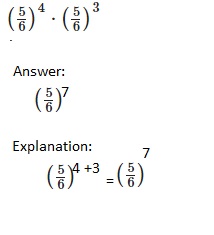
Question 19.
5m³n⁴ . 4m⁵n²
Answer:
20m⁸n⁶,

Explanation:
Given 5m³n⁴ . 4m⁵n² on solving 5 X 4 X m³⁺⁵ X n⁴⁺² = 20m⁸n⁶.

Question 20.
\(\left(\frac{7}{8}\right) \div\left(\frac{7}{8}\right)^{3}\)
Answer:

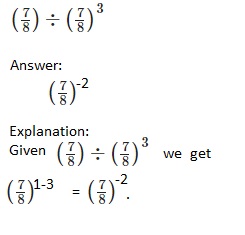
Question 21.
(-3)^-1 • (-3)°
Answer:
\(\frac{1}{-3}\),

Explanation:
Given (-3)^-1 . (-3)° as (-3)°  is 1 and (-3)^-1 value in positive exponent is
\(\frac{1}{-3}\).

Question 22.
x⁸z⁵ ÷ x³z⁹
Answer:
x⁵z^-4,

Explanation:
Given x⁸z⁵ ÷ x³z⁹ using division of product property
x^8-3z^5-9 we get x⁵z^-4.

Question 23.
25p⁶q⁹ ÷ 45p⁸q⁴
Answer:
5p^-2 q⁵ ÷ 9,

Explanation:
Given 25p⁶q⁹ ÷ 45p⁸q⁴
= 5p^6-8 q^9-4 ÷ 9,
= 5p^-2 q⁵ ÷ 9,

Question 24.
\(\left[\left(\frac{2}{3}\right)^{2} \cdot\left(\frac{2}{3}\right)^{-1}\right]^{3}\)
Answer:

Question 25.
40c⁵d³ ÷ 10c⁹d²
Answer:
4c^-4d,

Explanation:
Given 40c⁵d³ ÷ 10c⁹d² =4 X 10 X c^5-9 X d^3-2 ÷ 10 = 4c^-4d.

Question 26.

\(\left(\frac{72 b^{-1}}{32 c^{-1}}\right)^{-2}\)
Answer:

Question 27.
\(\frac{\left(9^{-2}\right)^{-2} \cdot 2^{2}}{9^{2}}\)
Answer:
9² X 2²,

Explanation:
Given

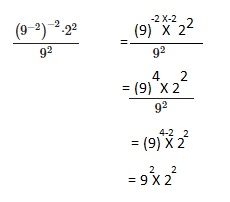
Question 28.
\(\frac{6^{8} \cdot 56^{-3}}{6^{5} \cdot 7^{-3}}\)
Answer:
6³ X 8^-3,

Explanation:

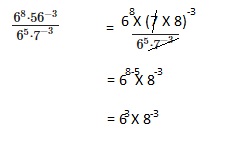
Question 29.
\(\frac{42^{-1}}{\left(2^{0}\right)^{12} \cdot 21^{-1}}\)
Answer:
2^-1,

Explanation:

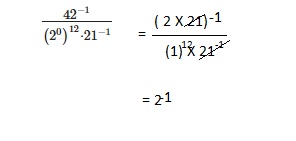
Question 30.
\(\frac{\left(3^{5} \cdot 3^{4}\right)^{2}}{\left(3^{3}\right)^{6}}\)
Answer:
1,

Explanation:

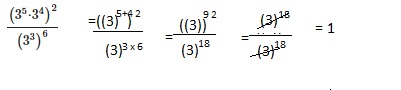
Solve each equation involving a variable that is squared.

Question 31.
r² = 256
Answer:
r = 16,

Explanation:

Question 32.
c² = \(\frac{121}{169}\)
Answer:
c = \(\frac{11}{13}\),

Explanation:
Given c² = \(\frac{121}{169}\)= \(\frac{11 X 11}{13 X 13}\),
c is sqaure root of \(\frac{11 X 11}{13 X 13}\) = \(\frac{11}{13}\).

Solve each equation involving a variable that is cubed.

Question 33.
x^{3 = 32.768
Answer:}
x = 3.2,

Explanation:

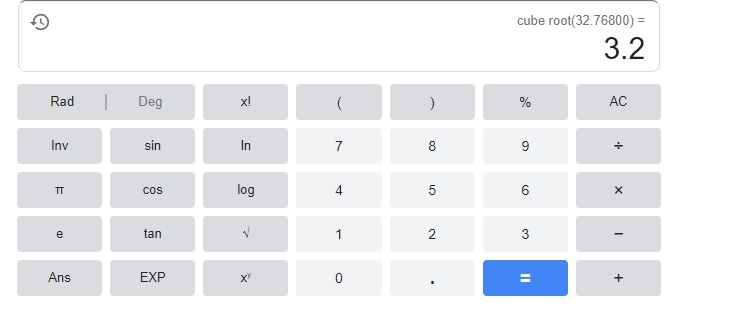
Question 34.
c³ = –\(\frac{27}{343}\)
Answer:
c= – \(\frac{3}{7}\),

Explanation:
Given c³ = –\(\frac{27}{343}\) can be written as
c³ = –\(\frac{3 X 3 X 3}{7 X 7 X 7}\) therefore c is cube root of
–\(\frac{3 X 3 X 3}{7 X 7 X 7}\) = – \(\frac{3}{7}\)

Question 35.
The expanded form of a number is 5 • 10¹ + 8 • 10° + 1 • 10^-1 + 9 • 10^-2. What is this number in standard form?
Answer:
The number in standard form is 58.19,

Explanation:
Given 5 • 10¹ + 8 • 10° + 1 • 10^-1 + 9 • 10^-2= 5 X 10 + 8 X 1 + 1 X 0.1 + 9 X 0.01 =
50 + 8 +0.1 + 0.09 = 58.19.

Question 36.
The pattern of triangles shown is called the Sierpinski’s gasket.
a) Find a pattern in the number of shaded triangles.
Answer:
(3/4)ⁿ,

Explanation:
The concept of the Sierpinski triangle is very simple:
Take a triangle. Create four triangles out of that one by connecting the centres of each side.
So basically each triangle cuts into four and each again cuts four and so on.
So, there are an infinite number of triangles pattern is (3/4)ⁿ.

b) How many shaded triangles will be in the fifth diagram of this pattern?
Write an exponential expression for this number.

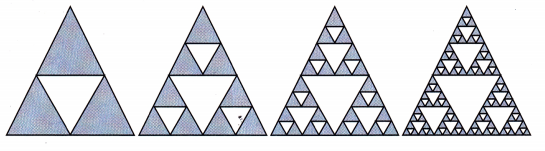
Answer:
Shaded triangles will be in the fifth diagram of this pattern are 243.
Explanation:
We have pattern(3/4)ⁿ here in first shape we have
3 shaded triangles out of 4, 5th pattern will have (3/4)⁵ so
shaded triangles will be in the fifth diagram of this pattern
3 X 3 X 3 X 3 X 3 = 243.

Problem Solving

Solve. Show your work. Round your answer to the nearest tenth.

Question 37.
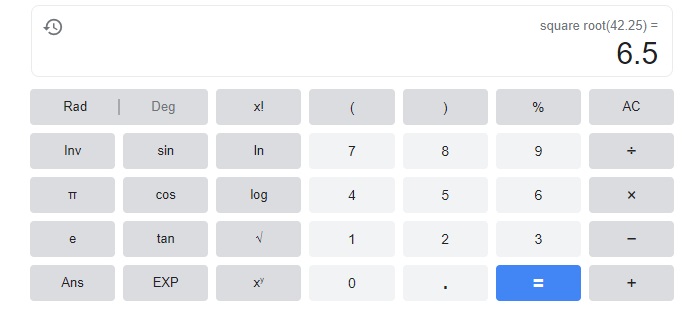
The Reina Sofia Museum in Spain has a glass elevator.
The floor of the elevator shaft is a square with an area of about 42.25 square feet.
Find the length of a side of the floor.
Answer:
The length of a side of the floor is 6.5 feet,

Explanation:
Given the Reina Sofia Museum in Spain has a glass elevator.
The floor of the elevator shaft is a square with an area of about 42.25 square feet.
The length of a side of the floor is 6.5 feet.

Question 38.
Earth’s volume is approximately 1,083,210,000,000 cubic kilometers.
What is the diameter of the Earth in kilometers?

Answer:
The diameter of the earth is 12,562 km ,

Explanation:
Given Earth’s volume is approximately 1,083,210,000,000 cubic kilometers.,
4/3pir³ = 1,08321 X 10^{7 ,}
we get r = 6281 kms,
therefore the diameter of the earth is 2 X 6281 km =  12,562 km.

Question 39.
Koch’s snowflake is a pattern that starts with an equilateral triangle.
Then, in successive images, each line segment is replaced by 4 line segments, as shown below.
How many line segments make up the seventh image of this pattern?
Write this number in exponential form and evaluate.

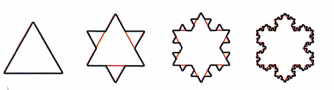
Answer:
3 X 4⁶,

Explanation:
Given Koch’s snowflake is a pattern that starts with an equilateral triangle.
Then, in successive images, each line segment is replaced by 4 line segments, as shown above.
we can express it in sequence of numbers
a1=3,
a2 = 3 X 4 = 12,
a3 = 3 X 4 X 4 = 48,
an = a^(n-1) X 4 = 4 a^(n-1),(geometric progression)
an = 3 x 4^(n-1),
n= 7
a7 = 3 X 4⁶.