This handy Math in Focus Grade 8 Workbook Answer Key Chapter 9 Review Test detailed solutions for the textbook questions.
Math in Focus Grade 8 Course 3 B Chapter 9 Review Test Answer Key
Concepts and Skills
Solve.
Question 1.
Name the triangle congruent to ∆ABC.
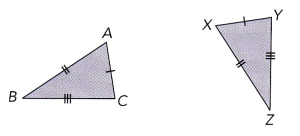
Answer:
∆XYZ
Explanation:
Given,
∆ABC is congruent to ∆XYZ
Question 2.
ABCDEF is a regular hexagon. Name a quadrilateral congruent to ADCB.
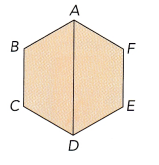
Answer:
ADEF
Explanation:
Given,
ABCDEF is a regular hexagon,
ADCB is congruent to ADEF
Question 3.
\(\overline{S Q}\) and \(\overline{T P}\) are straight lines. Name the triangle similar to ∆PQR.
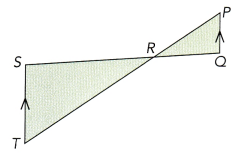
Answer:
∆TRS
Explanation:
Given,
∆PQR is congruent to ∆TRS
Solve. Show your work.
Question 4.
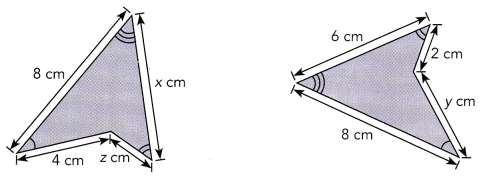
The two figures are congruent. Find the value of each variable,
a)
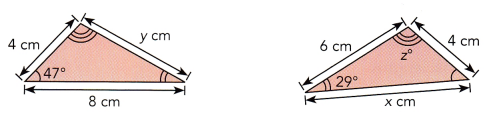
b)
Answer:
a) x = 8, y = 6, z = 104 degrees, b) x = 6, y = 4, z = 2
Explanation:
a) Since the triangles are congruent to each other, the longest side of the triangle measures 8 cm which is corresponding to the longest side of the second triangle which is x, therefore x = 8. While y is corresponding to the segment measuring 6 cm, therefore y = 6.
Solving z, the angle of 47 degrees corresponds to the other angle of the second triangle which is already having 29 degress, therefore the other triangle has 47 and 29 degress.
Sum of all the angles = 180 degrees
180 = 47 + 29 + z
180 = 76 + z
180 – 76 = z
104 = z
Therefore, x = 8, y = 6 and z = 104 degrees.
b)Since both the triangles are congruent to each other, the corresponding side of the second triangle is measuring 6 cm which is congruent to the first triangle of x, therefore x is measured as 6 cm. While y on the second triangle which is congruent to the first triangle which is measuring 4 cm, therefore y is measured as 4 cm. While z on the first triangle which is congruent to the first triangle’s measure of 2 cm, therefore, z is measured as 2 cm.
Therefore, x = 6, y = 4 and z = 2.
Question 5.
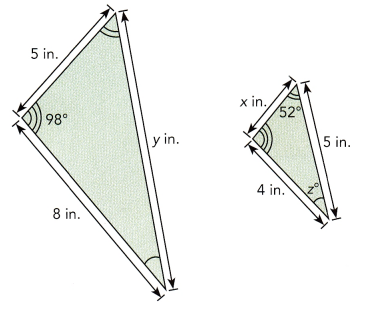
The two figures are similar. Find the value of each variable.
a)
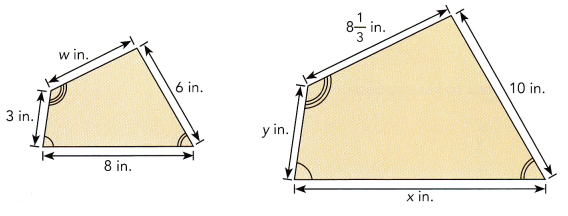
b)
Answer:
a) x = 2.5 inches, y = 10 inches and z = 30 degrees, b) w = 1.6, x = 13.3 inches and y = 1.8 inches.
Explanation:
a) Since the two triangles are similar the ratio of the corresponding lengths are equal, the side of the bigger triangle corresponds to x of smaller triangle.The side measuring 8 inches in the bigger triangle corresponds to the side of 4 inches in the smaller triangle.
Ratio of corresponding lengths are equal
5/x = 8/4
cross multiplying,
5 x 4 = 8 x X
20 = 8x
20/8 = x
2.5 = x
The side which measures y in the bigger triangle corresponds to the measure of 5 inches in the smaller triangle and the side of 8 inches in the bigger triangle corresponds to the side of 4 inches in the smaller triangle.
Ratio of corresponding lengths are equal
y/5 = 8/4
cross multiplying,
y x 4 = 8 x 5
4y = 40
y = 40/4
y = 10
Since the sum of all the angle in the triangle = 180 degrees
z + 52 degrees + p = 180 degrees
The other angle p whose measure is unknown corresponds to the angle in the larger triangle whose measure is 98 degrees, two triangles are similar, thus their angles are equal. So p is 98 degrees then,
Sum of the angles in the triangle = 180 degrees
180 = z + 52 + p
Substituting p = 98
180 = z + 52 + 98
180 = z + 150
z = 180 – 150
z = 30
Therefore, x = 2.5, y = 10, z = 30
b) Since both the triangles are similar, the ratio of their corresponding lengths are equal. The side which measures 10 inches in the bigger triangle corresponds to the side which measures 6 inches in the smaller triangle.The side which measures 8 1/3 in the smaller triangle corresponds to the w in the bigger triangle.
Ratio of corresponding lengths are equal
6/10 = w/ 8 1/3
cross multiplying,
6 x 8 1/3 = w x 10
16 = 10 w
w = 16/10
w = 1.6
The side which measures 10 inches in the bigger triangle corresponds to the side which measures 6 inches in the smaller triangle. The side which measures x inches in the bigger triangle corresponds to the side which measures 8 inches in the smaller triangle.
Ratio of corresponding lengths are equal
6/10 = 8/x
cross multiplying,
6 x X = 8 x 10
6x = 80
x = 80/6
x = 13.33
The side which measures 10 inches in the bigger triangle corresponds to the side which measures 6 inches in the smaller triangle. The side which measures y inches in the bigger triangle corresponds to the side which measures 3 inches in the smaller triangle.
Ratio of corresponding lengths are equal
6/10 = y/3
cross multiplying,
6 x 3 = y x 10
18 = 10y
18/10 = y
y = 1.8
Therefore, x = 13.33, y = 1.8 and w = 1.6
Question 6.
State whether the triangles are congruent. If they are congruent, write the statement of congruence and state the test used.
a)
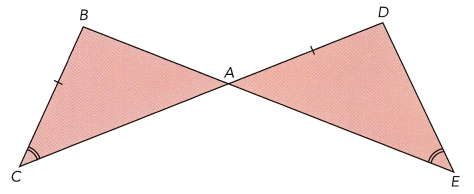
b)
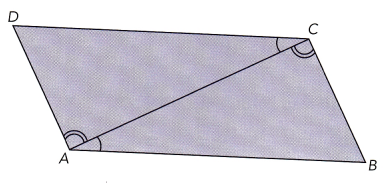
Answer:
a) The triangles are not congruent
Explanation:
The side BC and DA are congruent, however, the sides are not corresponding.
The side BA corresponds to DA but lines are not congruent,
BC corresponds to DC but lines are not congruent, therefore triangles are not congruent.
b) ∠C from ∆TRS corresponds to ∠A from ∆BCA and the two angles are congruent.
∠A from ∆DAC corresponds to ∠C from ∆BCA and the two angles are congruent.
Side AC from ∆DAC is congruent to side CA from ∆BCA.
By the Angle – Side – Angle Congruence Theorem, triangles are congruent.
This theorem states that two triangles are congruent and the sides in between these angles are congruent and corresponds to each other, then the triangle is congruent.
Question 7.
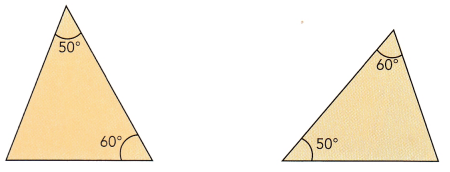
State whether the triangles are similar. Explain with a test for similar triangles.
a)
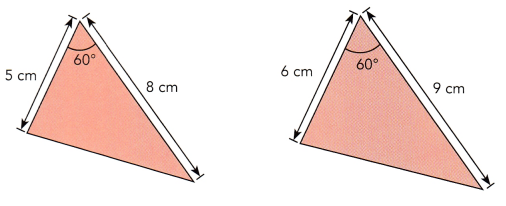
b)
Answer:
a) Triangles are similar
Explanation:
Both the triangles are similar triangles by Angle-Angle postulate, that states that triangles are similar if two pairs of their corresponding angles are congruent. For example, 60 degree angle of first triangle is corresponding the 60 degree angle of second triangle and also 50 degree angle of first triangle is corresponding the 50 degree angle of second triangle, then the two triangles are similar.
Therefore, triangles are similar.
b) Triangles are not similar
Explanation:
If the triangles are similar triangles by Side-Angle-Side postulate, then their two corresponding sides are proportional and their included angle is congruent. The included angles of two corresponding sides are congruent. However, the corresponding are not proportional, then the side measuring 5 cm corresponds to side measuring 6 cm, while side measuring 8 cm corresponds to side measuring 9 cm.
5/6 not equal to 8/9
0.83 not equal to 0.88
Therefore, Triangles are not similar.
Question 8.
∆ABC undergoes two reflections to be mapped onto ∆A”B”C”.
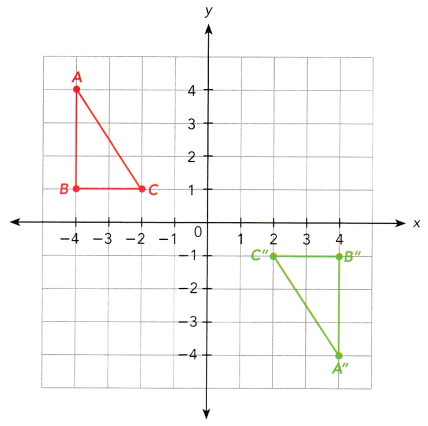
a) Describe one such pair of reflections.
Answer:
Since there are two reflections showing that A(-4,4) has been reflected into the x-axis and was mapped on to A'(-4,-4). The image of the first reflection is reflected in to the y-axis and shows A”(4, -4)
b) Describe a single transformation that would also map ∆ABC onto ∆A”B”C”.
Answer:
180 degree rotation changes the coordinates from (x,y) to (-x,-y).
Then A(-4, 4) mapped to (4, -4) B(-4, 1) mapped to (4, -1) and C(-2, 1) mapped to C(2, -1). The coordinates of the image of ∆ABC under the rotation of 180 degrees is actually ∆A”B”C”. Therefore, 180 degrees rotation maps the original triangle to ∆A”B”C” in a single transformation.
Describe the single transformations that maps ∆ABC onto ∆A’B’C’, ∆ A’B’C’ onto ∆A”B”C”, and ∆ABC onto ∆A”B”C”.
Question 9.
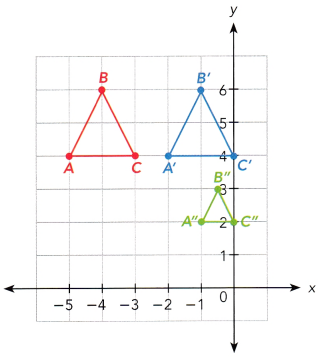
Answer:
i) For ∆ABC mapped to ∆A’B’C’, that the original points A(-5,4), B(-4,6) and C(-3,4). All the points move 3 units to the right. Therefore, transformation took place is translation.
ii) In ∆ABC mapped to ∆A”B”C”, the original points A(-5,4), B(-4,6) and C(-3,4) mapped to A”(-1, 2), B”(-0.5, 3) and C”(0, 2). ∆A”B”C” is smaller version of ∆ABC. If points A is connected on A”, B to B” and C on C” by the line, then the line should be extended until it makes an intersection, then this will meet on (2,0). Therefore, this transformation is dilation.
iii) For ∆A’B’C’ mapped to ∆A”B”C” original points A'(-2,4), B'(-1,6) and C(0,4) are mapped to A”(-1,2),B”(-0.5,3) and C”(0,2). ∆A”B”C” is a smaller version of ∆ABC. If points A is connected on A”, B to B” and C on C” by the line, then the line should be extended until it makes an intersection, then this will meet on (0,0). Therefore, this transformation is dilation.
Question 10.
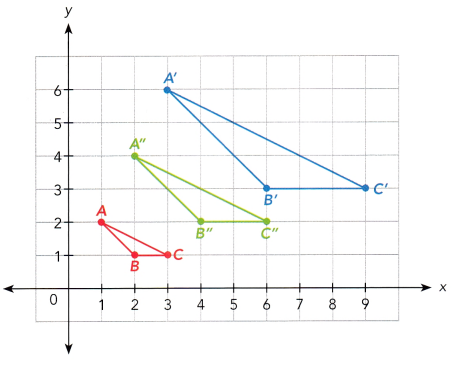
Answer:
i) For ∆ABC mapped to ∆A’B’C’, that the original points A(1,2), B(2,1) and C(3,1) are mapped to A'(3,6), B'(6,3) and C'(9,3).∆A’B’C’ is bigger version of ∆ABC If points A is connected on A”, B to B” and C on C” ” by the line, then the line should be extended until it makes an intersection, then this will meet on (0,0). Therefore, this transformation is dilation.
ii) In ∆A’B’C’ mapped to ∆A”B”C”, the original points A'(3,6), B'(6,3) and C'(9,3) mapped to A”(2,4), B”(4,2) and C”(6, 2). ∆A”B”C” is larger version of ∆A’B’C’. If points A is connected on A”, B to B” and C on C” by the line, then the line should be extended until it makes an intersection, then this will meet at the origin. Therefore, this transformation is dilation.
iii) For ∆ABC mapped to ∆A”B”C” original points A(1,2),B(2,1) and C(3,1) are mapped to A”(2,4),B”(4,2) and C”(6,2). ∆A”B”C” is a larger version of ∆ABC. If points A is connected on A”, B to B” and C on C” by the line, then the line should be extended until it makes an intersection, then this will meet on (0,0). Therefore, this transformation is dilation.
Question 11.
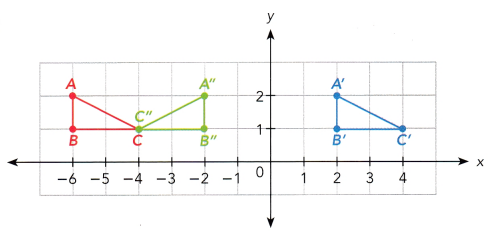
Answer:
i) For ∆ABC mapped to ∆A’B’C’, that the original points A(-6,2), B(-6,1) and C(-4,1) are mapped to A'(2,2), B'(2,1) and C'(4,1). All the points move 8 units to the right. Therefore, transformation took place is translation.
ii) In ∆A’B’C’ mapped to ∆A”B”C”, the original points A'(2,2), B'(2,1) and C'(4,1) mapped to A”(-2,2), B”(-2,1) and C”(-4,1). ∆A”B”C” is larger version of ∆A’B’C’. If points A is connected on A”, B to B” and C on C” by the line, then the line should be extended until it makes an intersection, then this will meet at the origin. Therefore, this transformation is dilation.
iii) For ∆ABC mapped to ∆A”B”C” original points A(-6,2),B(-6,1) and C(-4,1) are mapped to A”(-2,2),B”(-2,1) and C”(-4,1). The transformation is a reflection at x = -4. Both C and C” lies at -4 because 0 unit away, then so it is its image. A and B is 2 units to the left of -4 so A” and B” is 2 units to the right of it.
Problem Solving
Solve. Show your work.
Question 12.
Two geometrically similar buckets have bases with radii in the ratio 2 : 5. The top of the small bucket has radius 7 inches.
a) Find the radius of the top of the big bucket.
Answer:
The radius of the top of the big bucket
Explanation:
Given,
2 : 5 = 2/5
Let the radius be p,
7/p = 2/5
cross multiplying, 7 x 5 = 2 x p
35 = 2p
p = 35/2
p = 17.5
b) Write the ratio of the height of the small bucket to the height of the big bucket.
Answer:
Height of the small bucket/ Height of the big bucket
2 : 5
Question 13.
A 5-foot tall vertical rod and a 25-foot tall vertical flagpole stand on horizontal ground. At a certain time of the day, the flagpole casts a shadow 30 feet long.
a) Write a ratio comparing the height of the rod to the height of the flagpole.
Answer:
Height of rod/ Height of the flagpole
5/25 = 1/5
b) Calculate the length of the shadow cast by the rod.
Answer:
Let the length of the shadow of the rod be a,
Height of the rod/Height of flapole = Shadow length of the rod/Shadow length of the flagpole
5/25 = a/30
Cross multiplying, 5 x 30 = a x 25
125 = 25a
a = 125/25
a = 6
Question 14.
Two barrels are geometrically similar. Their heights are 16 inches and 20 inches. The diameter of the base of the larger barrel is 8 inches. Calculate the diameter of the base of the smaller barrel.
Answer:
Let t be the diameter of the base of smaller barrel,
Height of small barrel/ Height of large barrel = Diameter of small barrel/Diameter of large barrel
16 / 20 = t / 8
Cross multiplying, 16 x 8 = t x 20
128 = 20 t
128/20 = t
6.4 = t
Therefore, Diameter of the small barrel = 6.4 inches.
Question 15.
A photograph is 4 inches wide and 6 inches long. It is enlarged to a width 6 inches.
a) What is the length of the enlarged photo?
Answer:
The length of the enlarged photo is 9 inches
Explanation:
Let the length of the enlarged photo is r,
Width of the original photo/ Length of original photo = Width of enlarged photo/ Length of enlarged photo
4/6 = 6/r
cross multiplying, 4r = 6 x 6
4r = 36
r = 36/4
r = 9
b) If the original photo is enlarged to a length 12 inches, find the new width.
Answer:
New width = 8 inches
Explanation:
Let new width of the photo is i,
Width of the original photo/ length of the original photo = new width of the photo/ length of the photo
4/6 = i/12
Cross multiplying, 4 x 12 = i x 6
48 = 6i
i = 48/6
i = 8
Therefore, new width of the photo = 8 inches.
Question 16.
Anthony made an exact copy of the shape ABCDE using a photocopier.
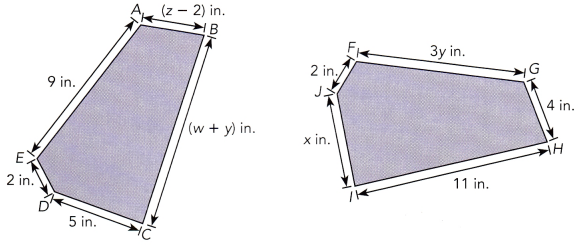
a) Name the shape congruent to ABCDE on the photocopy.
Answer:
GHIJF
Explanation:
Point A is congruent to point to G, Point B is congruent to point H, Point C is congruent to point I, Point D is congruent to point J, Point E is congruent to point F. Therefore, ABCDE is congruent to GHIJF.
b) Find the values for w, x, y, and z.
Answer:
w = 8, x = 5, y = 3, z = 6
Explanation:-
Solving x, IJ from GHIJF measuring x inches is congruent to CD of ABCDE which measures 5 inches.
IJ = CD
x = 5
Solving y, GF from GHIJF measuring 3y inches corresponds to AE from ABCDE which is measuring 9 inches.
GF = AE
3y = 9
divide 3 on both the sides
3y/3 = 9/3
y = 3
Solving z, HG from GHIJF measuring 4 inches corresponds to BA of ABCDE which is measuring (z – 2).
HG = BA
4 = (z – 2)
Adding 2 on both the sides
4 + 2 = z – 2 + 2
6 = z
Solving w, HI from GHIJH measuring 11 inches corresponds to BC of ABCDE which is measuring (w + y) inches.
HI = BC
11 = w + y
substituting y = 3,
11 = w + 3
Subtract 3 on both the sides,
11 – 3 = w + 3 – 3
8 = w.
Question 17.
A framed poster has a length of 28 inches and a perimeter of 88 inches. A similar poster has a perimeter of 66 inches. Find the area of the similar poster.
Answer:
Area of the similar poster = 252 sq inches
Explanation:
Let the length of the similar poster = p
length of similar poster/ length of framed poster = perimeter of similar poster/ perimeter of framed poster
substituting the values, p/28 = 66/88
cross multiplying, 88 x p = 66 x 28
88p = 1848
dividing 88 on both the sides, 88p/88 = 1848/88
p = 21
Therefore, length of the similar poster = 21 inches.
Perimeter of rectangle = 2 (l + w)
66 = 2 (21 + w)
66 = 42 + 2w
Subtracting 42 from both the sides,
66 – 42 = 42 + 2w – 42
24 = 2w
Divide 2 on both the sides,
24/2 = 2w/2
12 = w
Therefore, Width = 12 inches.
Area of rectangle = length x width
= 21 x 12
= 252 sq inches.
Question 18.
A robotic arm with two circular ends moves through a sequence of translations and rotations. The diagram shows two positions of the arm. All dimensions are in centimeters.

a) Find the values of x and y.
Answer:
x = 6 cm and y = 12 cm
Explanation:
The original image is exactly the same as transformed image, then the measure of the side of the original robotic arm is congruent to corresponding side of its image.
Solving for y:-
Side of original arm = Side of the image
substituting the expressions, y – 1 = 11
Adding 1 on both the sides, y – 1 + 1 = 11 + 1
y = 12
Therefore, y = 12 cm.
Solving for x:-
Other side of the original arm = other side of the image
Substituting the expressions, 2x = y
Substitute y = 12, 2x = 12
Divide 2 on both the sides, 2x/2 = 12/2
x = 6
Therefore, x = 6 cm
b) Calculate the area of the robotic arm. Use \(\frac{22}{7}\) as an approximation for π.
Answer:
Area of the robotic arm = 678.9 sq cm
Explanation:
Area of the arm = pi x diameter (diameter + length)
= 22/7 x 12 (12 + 6)
= 22/7 x 12 (18)
= 22/7 x 216
= 678.9 sq cm.
Question 19.
A table, which is in front of a mirror, has the side view ABCDEFGH shown below (all dimensions are in inches). ABCH and DEFG are rectangles. The side view is reflected in the mirror to form the congruent image STUVWXYZ.
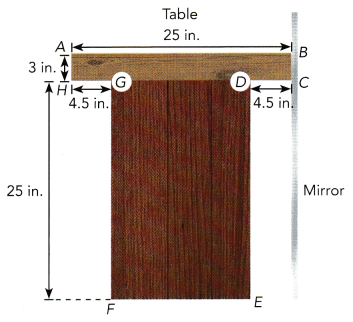
a) State the corresponding angle of ∠CDE and ∠AHG.
Answer: ∠V corresponds to ∠D and ∠Z corresponds to ∠H
Explanation:
Since ABCDEFGH is congruent to STUVWXYZ, the points A,B,C,D,E,F,G and H corresponds to S,T,U,V,W,X,Y and Z respectively.
Therefore, ∠V corresponds to ∠D and ∠Z corresponds to ∠H.
b) Write the length of \(\overline{T U}\), \(\overline{W X}\), and \(\overline{Y Z}\).
Answer:
TU = 3 inches, WX = 16 inches and YZ = 4.5 inches
Explanation:
i) As TU is congruent to BC of table ABCDEFGH, since BC measures 3 inches then TU also has 3 inches.
ii) WX is congruent to EF of table ABCDEFGH, to know the value of EF subtract the two measures of CD, GH to AB,Let the measure of AB = 25 inches and CD and GH = 4.5 inches then,
EF = AB – (CD + GH)
= 25 – ( 4.5 + 4.5 )
= 25 – 9
= 16
Since, EF measures 16 inches therefore, WX also measures 16 inches.
iii) YZ is congruent to GH of table ABCDEFGH, Since GH measures 4.5 inches therefore, YZ also measures 4.5 inches.
c) Find the perimeter of the image.
Answer:
Perimeter of STUVWXYZ = 106 inches.
Explanation:
Perimeter of ABCDEFGH = sum of all the lengths
Substituting all the sides of the table
Perimeter = AB + BC + CD + DF + EF + FG + GH + HA
Substituting all the values
Perimeter = 25 + 3 + 4.5 + 25 + 16 + 25 + 4.5 + 3
= 106
Therefore, the perimeter of ABCDEFGH is 106 inches and ABCDEFGH is congruent to STUVWXYZ then perimeter of STUVWXYZ is 106 inches
Question 20.
Gisele reduced the size of ∆PQR with area 14.4 square centimeters using a photocopier. ∆PQR ~ ∆STU.
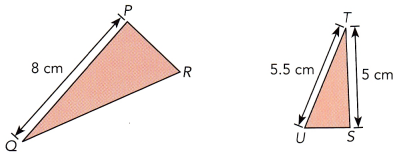
a) What is the scale factor of dilation? Express your answer as a percent.
Answer:
The scale factor of dilation is defined as the ratio of the size of the new image to the size of the old image.
Scale factor is 62.5%
Explanation:
PQ measuring 8 cm corresponds to side ST measuring 5 cm, to know the scale factor need to find the ratio of length of ST to length of PQ
Scale factor = length of ST/ length of PQ
= 5/8
= 0.625
Therefore, scale factor is 0.625
To convert it into percentage, multiply it with 100
Scale factor = 0.625 x 100
= 62.5%
b) Find the area of ∆STU.
Answer:
Area of ∆STU = 9 sq cm.
Explanation:
Two triangle are similar to each other,
Scale factor is 0.625,
Area of ∆PQR = 14.4 sq cm,
The area of ∆STU is given by the area of ∆PQR multiplied with scale factor.
Area of ∆STU = ∆PQR x scale factor
= 14.4 x 0.625
= 9