Practice the problems of Math in Focus Grade 8 Workbook Answer Key Cumulative Review Chapters 5-6 to score better marks in the exam.
Math in Focus Grade 8 Course 3 A Cumulative Review Chapters 5-6 Answer Key
Concepts and Skills
Solve each system of linear equations by making tables of values. Each variable x is a positive integer less than 7. (Lesson 5.1)
Question 1.
4x + 3y = 23
y – 2x = 1
Answer:
Given the linear equations,
4x + 3y = 23
y – 2x = 1
4(y – 2x = 1)
2y – 4x = 2
4x + 3y = 23
-4x + 2y= 2
5y = 25
y = 5
substitute the value of x in the above equation.
(5) – 2x = 1
5 – 2x = 1
-2x = 1 – 5
-2x = -4
x = 2
Thus the value of x is 2 and y is 5
Question 2.
4y + 3x = 19
x + y = 5
Answer:
Given,
4y + 3x = 19
x + y = 5
Rewrite them as
3x + 4y = 19
3x + 3y = 15
– – –
0x + y = 4
y = 4
substitute the value of y in the above equation
x + 4 = 5
x = 5 – 4
x = 1
Solve each system of linear equations by using the elimination or substitution method. Explain your choice of method. (Lesson 5.2)
Question 3.
3a – 2b = 1
2a + 3b = 18
Answer:
Given,
3a – 2b = 1—- (×2)
2a + 3b = 18–(×3)
6a – 4b = 2
6a + 6b = 36
– – –
0a – 10b = -34
10b = 34
b = 3.4
substitution the value of b in the equation
3a – 2(3.4) = 1
3a – 6.8 = 1
3a = 1 + 6.8
3a = 7.8
a = 2.6
substitution method
Question 4.
0.7x – 1.2y = -11.5
0.5x + 3.5y = 31
Answer:
Given,
0.7x – 1.2y = -11.5
0.5x + 3.5y = 31
5 (0.7x – 1.2y = -11.5)
0.35x – 6y = -57.5
7(0.5x + 3.5y = 31)
0.35x + 24.5y = 217
0.35x – 6y = -57.5
– + +
0x + 30.5y = 274.5
30.5y = 274.5
y = 274.5/30.5
y = 9
Now substitute the value of y in the above equation.
0.5x + 3.5(9) = 31
0.5x = 31 – 31.5
0.5x = -0.5
x = -0.5/0.5
x = -1
Substitution method is used to solve the given equations.
Question 5.
\(\frac{1}{4}\)h + \(\frac{2}{3}\)k = 5
\(\frac{3}{4}\)h + k = 6
Answer:
Given,
\(\frac{1}{4}\)h + \(\frac{2}{3}\)k = 5
\(\frac{3}{4}\)h + k = 6
\(\frac{2}{3}\) \(\frac{3}{4}\)h + \(\frac{2}{3}\)k = 6 . \(\frac{2}{3}\)
Now solve both the equations
\(\frac{1}{4}\)h + \(\frac{2}{3}\)k = 5
\(\frac{1}{2}\)h + \(\frac{2}{3}\)k = 4
\(\frac{1}{4}\)h + 0 = 1
h = 1/\(\frac{1}{4}\)
h = 4
Now substitute the value of h in the above equation
\(\frac{3}{4}\)(4) + k = 6
3 + k = 6
k = 6 – 3
k = 3
The substitution method is used to solve the given equations.
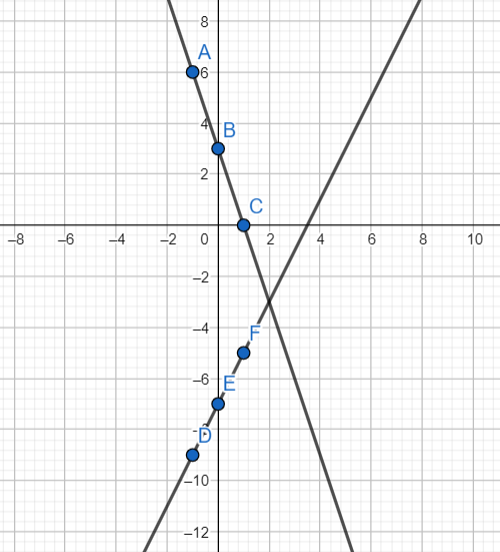
Solve each system of linear equations by using the graphical method. Use 1 grid square on both axes to represent 1 unit for the interval from -5 to 10. (Lesson 5.4)
Question 6.
3x + y = 3
4x – 2y = 14
Answer:
Given,
3x + y = 3
4x – 2y = 14
3x + y = 3— × (2)
6x + 2y = 6 —- (eq. 3)
Solving eq. 3 and 2
6x + 2y = 6
4x – 2y = 14
10x = 20
x = 20/10
x = 2
3(2) + y = 3
6 + y = 3
y = 3 – 6
y = -3
3x + y = 3
| X | -1 | 0 | 1 |
| y | 3(-1) + y = 3 -3 + y = 3 y = 6 |
3(0) + y = 3 y = 3 |
3(1) + y = 3 3 + y = 3 y = 0 |
4x – 2y = 14
| X | -1 | 0 | 1 |
| y | 4(-1) – 2y = 14 -4 – 2y = 14 -2y = 18 y = -9 |
4(0) – 2y = 14 -2y = 14 y = -7 |
4(1) – 2y = 14 4 – 2y = 14 -2y = 10 y = -5 |
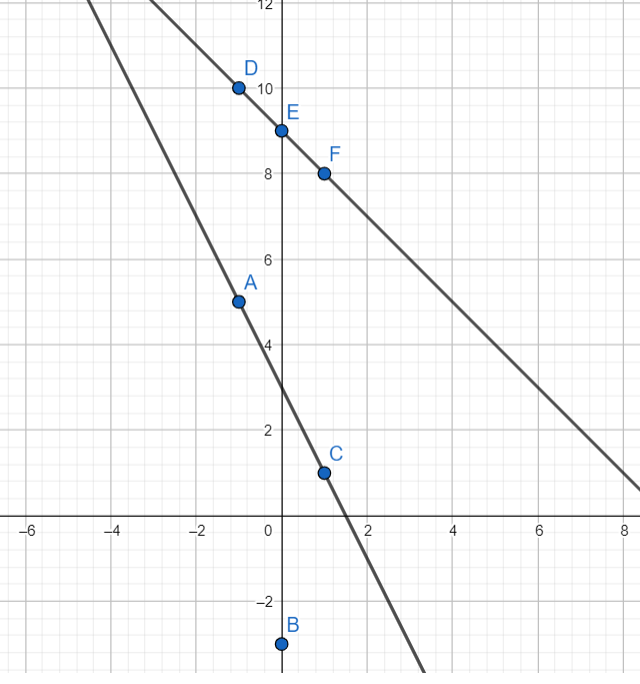
Question 7.
2x – y = 3
x + y = 9
Answer:
Given,
2x – y = 3
x + y = 9
3x = 12
x = 4
4 + y = 9
y = 9 – 4
y = 5
| x | -1 | 0 | 1 |
| y | 2(-1) – y = 3 -2 – y = 3 y = 5 |
2(0) – y = 3 y = -3 |
2(1) – y = 3 2 – y = 3 y = 1 |
x + y = 9
| x | -1 | 0 | 1 |
| y | -1 + y = 9 y = 10 |
0 + y = 9 y = 9 |
1 + y = 9 y = 8 |
Question 8.
2x + y = 25
3x – 4y = – 1
Answer:
Given,
2x + y = 25— eq. 1
3x – 4y = – 1—- eq. 2
Solve the equations 1 & 2
2x + y = 25 —× 4
8x + 4y = 100—(eq. 3)
3x – 4y = – 1
Solving equations 3 and 2
8x + 4y = 100
3x – 4y = – 1
11x = 99
x = 99/11
x = 9
Substitute the value of 9 in eq. 1
2(9) + y = 25
y = 25 – 18
y = 7
Identify whether each system of linear equations is inconsistent or dependent. Justify your answer. (Lesson 5.5)
Question 9.
3x + 4y = 12
\(\frac{3}{4}\)x + y = 3
Answer:
Given,
3x + 4y = 12
\(\frac{3}{4}\)x + y = 3
3x + 4y = 12
Dependent
After multiplying equation 2 by 4, the equations are 3x + 4y = 12
Thus the equations are equivalent
Question 10.
0.2x + 1.2 = y
x + 8 = 5y
Answer:
Given,
0.2x + 1.2 = y
x + 8 = 5y
0.2x – y = 1.2 — × 5
x – 5y = 6
x – 5y = -8
0
Inconsistent
Question 11.
3x + 2y = \(\frac{1}{3}\)
9x + 6y = 1
Answer:
Given,
3x + 2y = \(\frac{1}{3}\)
9x + 6y = 1
9x + 6y = 1
Dependent
Thus the equations are equivalent
Tell whether the relation in each mapping diagram, table, or graph is a function. Explain. (Lesson 6.1)
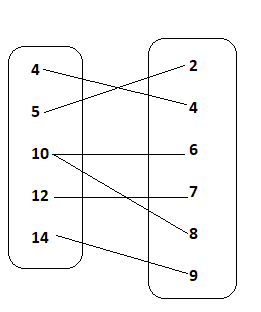
Question 12.
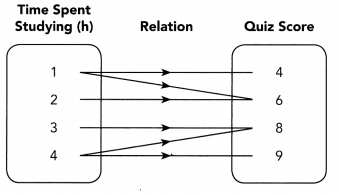
Answer:
No, because the output has more than one value.
Question 13.

Answer:
Yes because each input has exactly one output, it is a function.
Question 14.
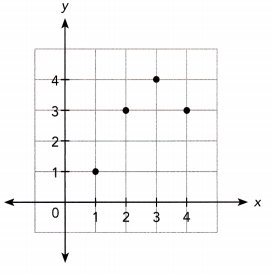
Answer:
Yes because each input has exactly one output, it is a function.
Question 15.
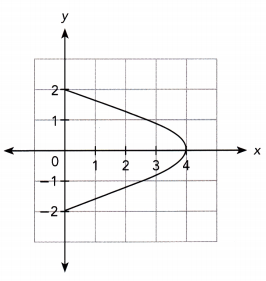
Answer:
No because, at least one vertical line intersects the graph at more than one point, it is not a function.
Write an algebraic equation for each function. (Lesson 6.2)
Question 16.
A chef makes 100 hot dog buns each morning. In the afternoons, he makes 40 hot dog buns per hour. The total number of hot dog buns he makes each day, y, is a function of the time he takes to make the buns in the afternoons, x hours.
Answer:
40x
Th number of hot dog buns made in the afternoons is the product between number of hours x and the rate of 40 hot dog buns per hour:
y = 100 + 40x
The total number of hot dogs buns per day is the sum between the number of hot dogs buns made in the morning and the number of hot dogs buns made in the afternoon:
Question 17.
Gina walks 2 kilometers from home to a park. She then jogs at an average speed of 7 kilometers per hour. The total distance she traveled, d kilometers, ¡s a function of the time she takes to jog, t hours.
Answer:
Given,
Gina walks 2 kilometers from home to a park. She then jogs at an average speed of 7 kilometers per hour.
The total distance she traveled, d kilometers, is a function of the time she takes to jog, t hours.
d = 2 + 7t
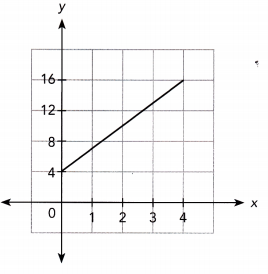
Question 18.
Answer:
The graph being a line, the function is Linear. Its slope-intercept equation S:
y = mx + b
We determine the slope m using the sLope formula and the points (0, 4) and (4, 16):
m = \(\frac{16-4}{4-0}\)
= \(\frac{12}{4}\)
= 3
The graph intersects the y-axis in (0, 4), so the y-intercept is 4:
b = 4
The line’s equation is:
y = 3x + 4
Question 19.
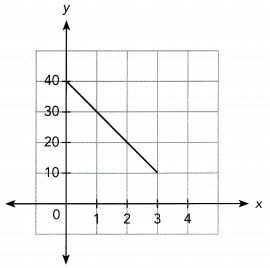
Answer: y = -10x + 40
Tell whether each table, equation, or graph represents a linear function. If so, find the rate of change. Then tell whether the function is increasing or decreasing. (Lesson 6.3)
Question 20.
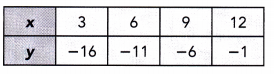
Answer: Yes, It is increasing
Question 21.

Answer:
No; it is decreasing
Question 22.
3y + 2x = 10
Answer:
No, it is decreasing
Question 23.
V = l3, l > 0
Answer: no; increasing
Question 24.
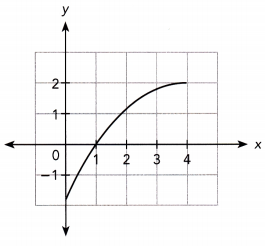
Answer: Yes, it is decreasing
Question 25.
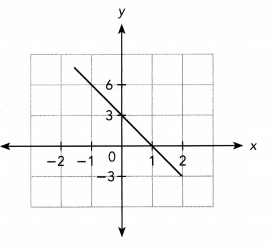
Answer:
Yes; decreasing
Problem Solving
Solve. Show your work.
Question 26.
A school librarian keeps track of the number of students in the library at any one time, and the number of computers being used. The table shows the data she collected for one day. (Chapter 6)

Draw a mapping diagram to represent the relation between the number of students in the library and the number of computers being used. Is this relation a function? Explain.
Answer:
It is a one to many relation.
Question 27.
Find two numbers whose sum is 60, such that twice the lesser number is equal to half of the greater number. (Chapter 5)
Answer:
Let the two numbers be x and 4x
x + 4x = 60
5x = 60
x = 60/5
x = 12
4x = 4(12) = 48
Question 28.
The diagram shows a parallelogram with side lengths in inches. (Chapter 5)
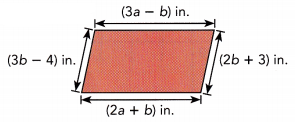
a) Find the values of a and b.
Answer:
3b – 4 + 2b + 3
5b – 1
b = 1/5 inch.
(3a – b) + (2a + b)
5a
b) Find the perimeter of the parallelogram.
Answer:
perimeter of the parallelogram = 2(a + b)
p = 2 (5b – 1 + 5a)
p = 10a + 10b – 2
Question 29.
Glenn donates $50 to a charity. In addition, he pledges to donate $2 per month beginning this month. The total amount he donates, y dollars, is a function of the number of months he donates, x months. (Chapter 6)
a) Write an algebraic equation for the function.
Answer: y = 50 + 2x
b) Graph the function and draw a line through the points. Use 1 unit on the horizontal axis to represent 1 month for the x interval from 0 to 6, and 1 unit on the vertical axis to represent $2 for the y interval from 50 to 62. Do the coordinates of every point on the line make sense for the function? Explain.
Answer:
| Number of months | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Total amount | 50 | 52 | 54 | 56 | 58 | 60 | 62 |
No, only whole numbers are meaningful for the input and output. The input values, which are the number of months must be whole numbers. Hence, the corresponding output values of the function are also whole numbers.
c) Describe how the slope and y-intercept of the graph are related to the function.
Answer:
The y-intercept, 50 means that Glenn donated $50 to the charity at first. The slope 2, gives the rate that he donates per month. For every month that passes, the total amount that he donated increases by $2.
Question 30.
In a stationery store, 15 pencils and 20 rulers are sold for $20.50. Jennifer buys 7 pencils and 2 rulers for $5.90. Find the price of each item. (Chapter 5)
Answer:
Let the cost of the pencil be x
Let the cost of rulers be y
15x + 20y = 50
7x + 2y = 5.90—- × 10
70x + 20y = 59—Eq.3
Solving and eq. 3 – 1
70x + 20y = 59
15x + 20y = 50
55x = 9
x = 9/55
x = 0.16
Thus the cost of each pencil is $0.16
7(0.16) + 2y = 5.90
1.12 + 2y = 5.90
2y = 5.90 – 1.12
2y = 4.78
y = 2.39
Thus the cost of the rulers is $2.39
Question 31.
A group of 70 students and teachers visited a theme park. The teachers were charged a regular price of $50 per ticket. A 30% count of the regular ticket price was given to each student. The total ticket price for the whole group cost $2,600. Find the number of students and teachers in the group. (Chapter 5)
Answer:
Let’s note:
t = the number of teachers
s = the number of students
The total number of persons in the group:
t + s = 70 Equation 1
The cost of all tickets:
50t + (1 – 0.30)50s = 2600
50t + 35s = 2600 Equation 2
We write the system:
t + s = 70 Equation 1
50t + 35s = 2600 Equation 2
We use the substitution method
t + s = 70
We express t in terms of s from Equation 1:
t + s – s = 70 – s
t = 70 – s Equation 3
Substitute Equation 3 in Equation 2 and determine s:
50(70 – s) + 35s = 2600
3500 – 50s + 35s = 2600
3500 – 15s = 2600
3500 – 15s – 3500 = 2600 – 3500
-15s = -900
\(\frac{-15 s}{-15}\) = \(\frac{-900}{-15}\)
s = 60
Substitute s in Equation 1 to determine t:
t = 70 – 60
= 10
The number of students is 60 and the number of teachers is 10.
Question 32.
The fuel tank in Tasha’s car can hold up to 8 gallons of gasoline. She can drive a distance of 40 miles for each galIf gasoline. The total amount of gasoline in her fuel tank, y gallons, is a function of the distance she drives, x miles. (Chapter 6)
a) Give the least possible input value and the corresponding output value. Tell whether the function is linear or nonlinear. Then tell whether the function is increasing or decreasing. Explain.
Answer:
At the initial moment the tank is full, therefore it has 8 gallons. As the car moves, the amount of gasoline decreases by 1 gallon for each 40 miles, therefore it is linear and decreasing. The Least possible input value is 0 (the initial distance). The corresponding output value is 8 gallons.
x = 0 miles
y = 8 gallons
b) Sketch a graph for the function. Identify the y-intercept of the graph.
Answer:
The graph starts at (0; 8) and falls to the right with the slope \(\frac{1}{40}\).
y = mx + b
y = –\(\frac{1}{40}\)x + 8
We graph the function.
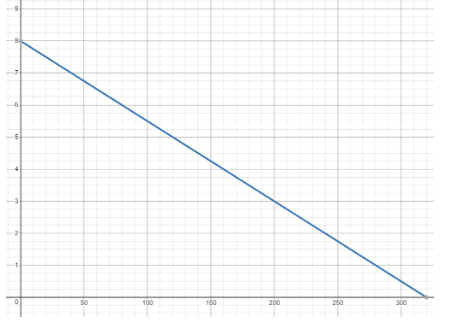
The y-intercept is b = 8.
Question 33.
The pressure in two tanks increases at a constant rate of 2 bars per minute. The initial pressure in Tank A is 3 bars. The pressure in Tank B is 14 bars after 3 minutes. (Chapter 5)
a) Write a system of two linear equations for the pressure p in the two tanks in terms of the time t.
Answer:
The pressure in two tanks increases at a constant rate of 2 bars per minute.
The initial pressure in Tank A is 3 bars.
Tank A: p = 2t + 3
The pressure in Tank B is 14 bars after 3 minutes.
Tank B: p = 2t + 8
b) Graph the two equations on a coordinate plane. Use 1 grid square on both axes to represent 1 unit for the interval from 0 to 5.
Answer:
We graph the two functions on a coordinate plane:
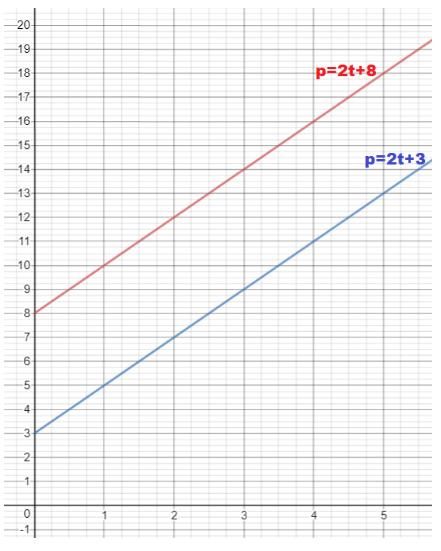
c) When will the pressure in both tanks be the same? How do you know?
Answer:
The pressure in both tanks will not be the same.
The two lines are parallel.
Question 34.
Mr. Johannsen wants to compare how fast water evaporates from two inflatable swimming pools, A and B, placed at different locations. The height of the water level in each pool, h inches, is a function of the time it takes for the water to evaporate, t days. (Chapter 6)
Pool A

Pool B
An initial water level of 24 inches where water evaporates at a rate of 0.4 inch per day
a) Write an algebraic equation to represent each function.
Answer:
We are given the function for pool A:

We have:
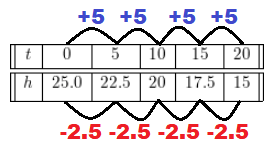
The rate of change is:
\(\frac{-2.5}{5}\) = -0.5
\(\frac{-2.5}{5}\) = -0.5
\(\frac{-2.5}{5}\) = -0.5
\(\frac{-2.5}{5}\) = -0.5
Because the rate of change for the function is constant the table represents a linear function. Its slope is:
m = -0.5
We determine the y-intercept using the fact that the graph passes through the point (0.25):
b = 25
Substitute m, b to determine the equation:
h = -0.5t + 25
We determine the equation for Pool B, using the y-intercept 24 and the slope -0.4:
h = -0.4t + 24
b) Graph the two functions on the same coordinate grid. Use 1 unit on the horizontal axis to represent 5 days for the t interval from 0 to 20, and 1 unit on the vertical axis to represent 1 inch for the h interval from 15 to 25.
Answer:
We graph the two functions:
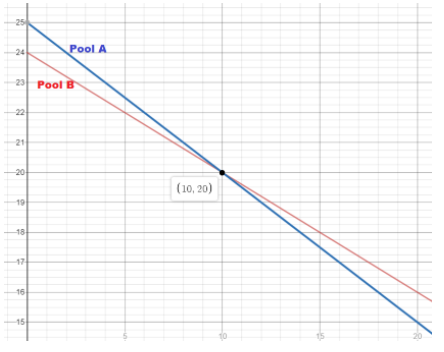
c) Use a verbal description to compare the two functions.
Answer:
Both functions are linear and decreasing.
The initial height of the water in Pool A is greater than that of Pool B, but the rate of water evaporation is higher for Pool A. After 10 days the height of the water in Pool A is smaller than that of Pool B.