Math in Focus Grade 8 Chapter 7 Answer Key The Pythagorean Theorem

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 7 The Pythagorean Theorem to score better marks in the exam.

Math in Focus Grade 8 Course 3 A Chapter 7 Answer Key The Pythagorean Theorem

Math in Focus Grade 8 Chapter 7 Quick Check Answer Key

Find the square of each number.

Question 1.
3
Answer:
9,

Explanation:
Given number is 3 the square is 3² = 3 X 3 = 9.

Question 2.
\(\frac{1}{4}\)
Answer:
\(\frac{1}{16}\),

Explanation:
Given number is \(\frac{1}{4}\) the sqaure is
(\(\frac{1}{4}\))² = \(\frac{1}{4}\) X \(\frac{1}{4}\) =
\(\frac{1 X 1}{4 X 4}\) = \(\frac{1}{16}\).

Question 3.
-7
Answer:
49,

Explanation:
Given number is -7 the square is (-7)² = -7 X -7 = 49.

Find the square roots of each number.

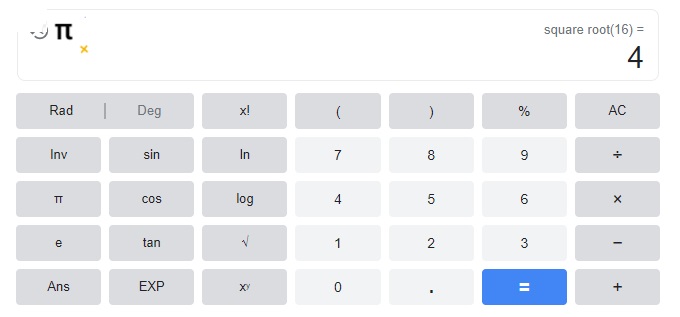
Question 4.
16
Answer:
4,

Explanation:

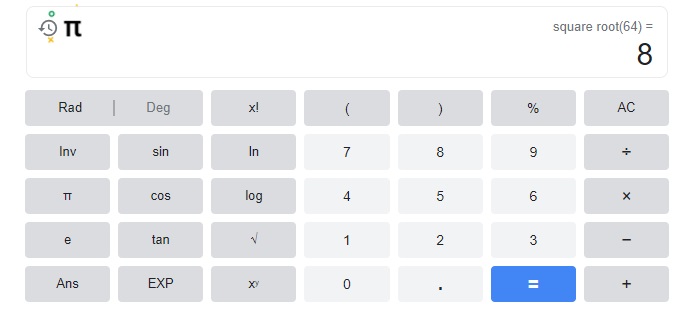
Question 5.
64
Answer:
8,

Explanation:

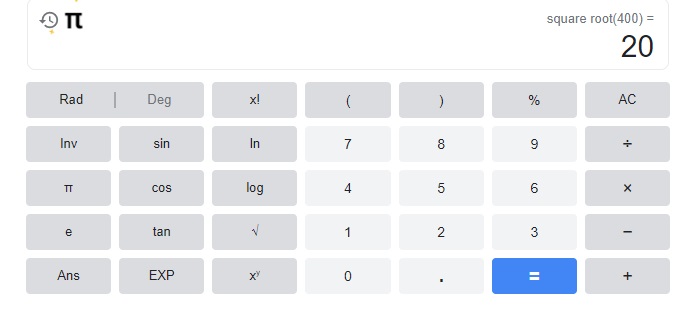
Question 6.
400
Answer:
20,

Explanation:

Find the cube of each number.

Question 7.
\(\frac{1}{2}\)
Answer:
\(\frac{1}{8}\),

Explanation:
Given \(\frac{1}{2}\) the cube is (\(\frac{1}{2}\))³ =
\(\frac{1}{2}\) X \(\frac{1}{2}\) X \(\frac{1}{2}\) =
\(\frac{1 X 1 x 1}{2X 2 X 2}\) =\(\frac{1}{8}\).

Question 8.
7
Answer:
343

Explanation:
Given 7 the cube is (7)³ = 7 X 7 X 7 = 343.

Question 9.
11
Answer:
1331,

Explanation:
Given 11 the cube is (11)³ = 11 X 11 X 11 = 1331.

Find the cube root of each number.

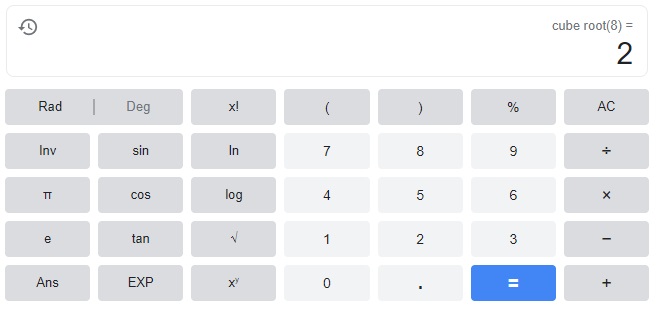
Question 10.
8
Answer:
2

Explanation:

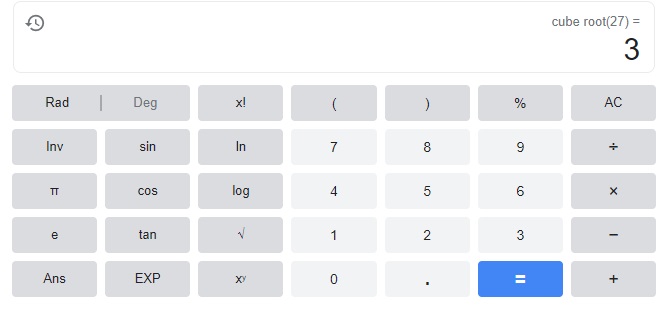
Question 11.
27
Answer:
3

Explanation:

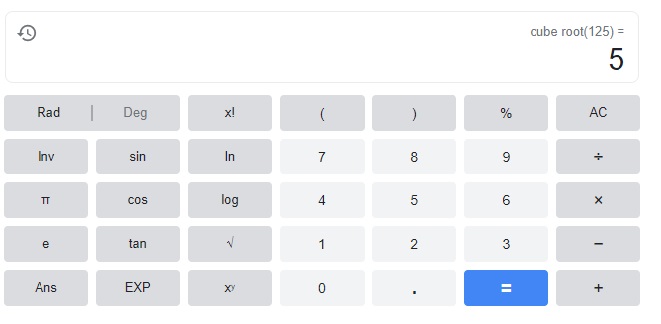
Question 12.
125
Answer:
5

Explanation:

Use graph paper. Plot each pair of points on a coordinate plane. Connect the points to form a line segment and find its length.

Question 13.
(3, 5) and (3, 9)
Answer:
The objective is to plot and connect point (-3, 1) and point(-3, -3) on a coordinate plane, then identify the length of the line that the two points create.

Note that to represent point (-3, 1), point out in which part of the graph does -3 and 1 meet. -3 is 3 units to the left of 0 and 1 is 1 unit up. Likewise, for point (-3, -3), point out in which part of the graph does -3 and -3 meet. The first -3 is 3 units to the left of 0 and the other -3 is 3 units down. Then, let O be the point (-3, 1), and P be the point (-3, -3).

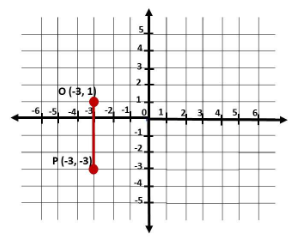
To find the length of the line segment \(\overline{O P}\), get the absolute value of the difference of y-coordinate of point O  to the y-coordinate of P since points O and P have the same x-coordinate which is -3. Then
length of \(\overline{O P}\) = |1 – (-3)|
= |1 + 3|
= 4
Therefore, the length of \(\overline{O P}\) is 4 units.

Question 14.
(3, -6) and (3, -9)
Answer:
The goal of this task is to plot and connect point (1, 2) and point (1, -1) on a coordinate plane, then identify the length of the line that the two points create.

Notice that to show point (1, 2), specify in which part of the graph does 1 and 2 meet. 1 is 1 unit to the right of 0 and 2 is 2 units up. Likewise, for point (1, -1), specify in which part of the graph does 1 and -1 meet 1 is 1 unit to the right of 0 and -1 is 1 unit down. Then, Let Q be the point (1, 2), and R be the point (1, -1).

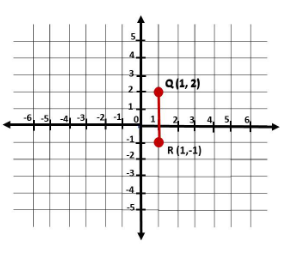
To find the length of the line segment \(\overline{Q R}\), get the absolute value of the difference of y-coordinate of point Q  to the y-coordinate of R since points Q and R have the same x-coordinate which is 1. Then
length of \(\overline{Q R}\) = |2 – (-1)|
= |2 + 1|
= 3
Therefore, the length of \(\overline{Q R}\) is 3 units.

Question 15.
(-4, 9) and (-8, 9)
Answer:
The target of this task is to plot and connect point (1, -3) and point (5, -3) on a coordinate plane, then identify the length of the line that the two points create.

Observe that to represent point (1, -3), point out in which part of the graph does 1 and -3 meet 1 is 1 unit to the right of 0 and -3 is 3 units down. Likewise, for point (5, -3), point out in which part of the graph does 5 and -3 meet 5 is 5 units to the right of 0 and -3 is 3 units down Then, let S be the point (1, -3), and T be the point (5, -3).

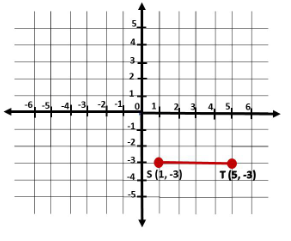
Now, to find the length of the line segment \(\overline{S T}\), get the absolute value of the difference of x-coordinate 1 of point S to the x-coordinate of T since points S and T have the same y-coordinate which is -3. Then
length of \(\overline{S T}\) = |1 – 5|
= |-4|
= 4
Therefore, the length of \(\overline{S T}\) is 4 units.

Question 16.
(-2, 5) and (8, 5)
Answer:
The objective of this task is to plot and connect point (-5, 3) and point (5, 3) on a coordinate plane, then identify the
length of the line that the two points create.

Note that to show point (-5, 3), specify in which part of the graph does -5 and 3 meet -5 is 5 units to the left of 0 and 3 is 3 units up. Likewise, for point (5, 3), specify in which part of the graph does 5 and 3 meet 5 is 5 units to the right of 0 and 3 is 3 units up. Then, let U be the point (-5, 3), and V be the point (5, 3).

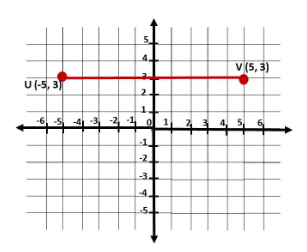
Next, to determine the length of the Line segment \(\overline{U V}\), get the absolute value of the difference of x-coordinate of point U to the x-coordinate of V since points U and V have the same y-coordinate 3. Then
length of \(\overline{U V}\) = |-5 – (5)|
= |-5 + -5|
= |-10|
= 10
Therefore, the length of \(\overline{U V}\) is 10 units.

Find the volume of each solid. Use 3.14 as an approximation for π. Round your answers to the nearest tenth if necessary.

Question 17.

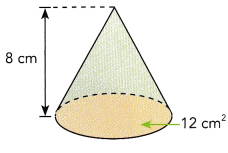
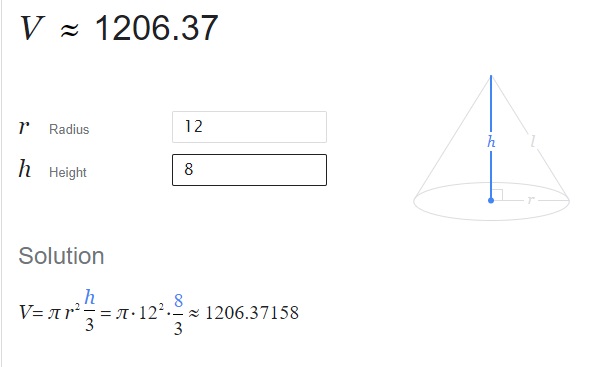
Answer:
Volume of cone ≈ 1206.37 cm³ ,

Explanation:

Question 18.

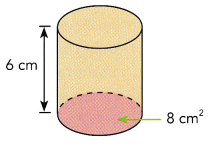
Answer:
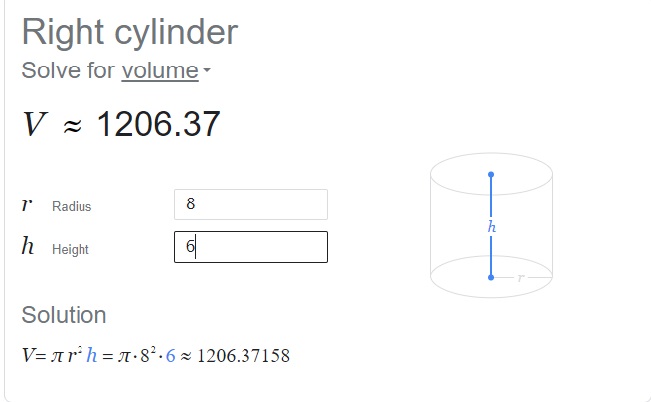
The volume of cylinder ≈1206.37 cm³ ,

Question 19.

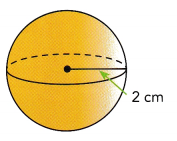
Answer:
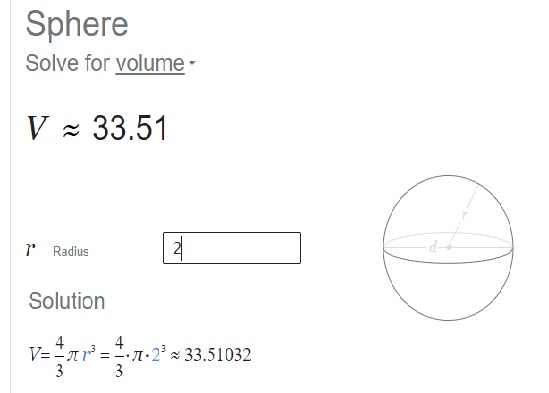
Volume of sphere is ≈33.51 cm³,

Explanation:

Question 20.

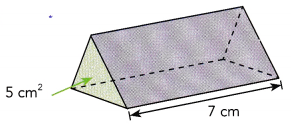
Answer:
Volume of triangular prism is 35 cm³ ,

Explanation:
Volume of triangular prism = area of cross-section X length,
5 cm²  × 7 cm = 35 cm³.

Question 21.

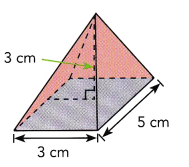
Answer:
Volume of Pyramid is 15 cm³,

Explanation: