Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 7 Lesson 7.1 Understanding the Pythagorean Theorem and Plane Figures to score better marks in the exam.
Math in Focus Grade 7 Course 3 B Chapter 7 Lesson 7.1 Answer Key Understanding the Pythagorean Theorem and Plane Figures
Math in Focus Grade 8 Chapter 7 Lesson 7.1 Guided Practice Answer Key
Hands-On Activity
Materials:
- scissors
Use Rearrangementto Prove The Pythagorean Theorem
In a right triangle, the longest side is known as the hypotenuse. The two shorter sides are called legs.
Step 1.
Draw four identical right triangles, with side lengths a, b, and c, on a a piece of paper and cut them out. Make one leg shorter than the other.
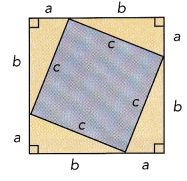
Step 2.
Arrange the triangles to form a square with side length c.
Step 3.
What is the area of the square whose sides are c units long? Label the large square with its area.
Step 4.
Draw two squares on a different piece of paper. One square should have side lengths of b units, and the other should have side lengths of a units. You can use one of the triangles as a guide to mark off a units and b units. Cut out these square and arrange the four triangles and the two new squares to form a large square like the one shown.
Step 5.
Write an algebraic expression in terms of a and b for the combined area of the two small squares.
Math Journal Compare the areas of the squares found in Step 3 and Step 5. Write an equation that relates the area of one square to the sum of the areas of the other two squares.
In the activity, you explored the relationship among the sides of a right triangle. This relationship is true for all right triangles and is described by the Pythagorean Theorem.

In the activity, you observed the following:
Pythagorean Theorem
The square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of the two legs. For the triangle shown, you can write this equation: a2 + b2 = c2.
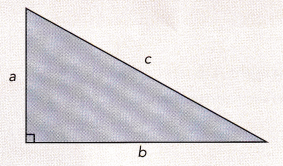
Complete.
Question 1.
Merlin wants to put a fence around a right triangular garden.
He measures two sides. Find the length of the unknown side.

Answer:
The length of the unknown side is 15 ft,
Explanation:

Complete.
Question 2.
Find the values of x and y. Round your answer to the nearest tenth.
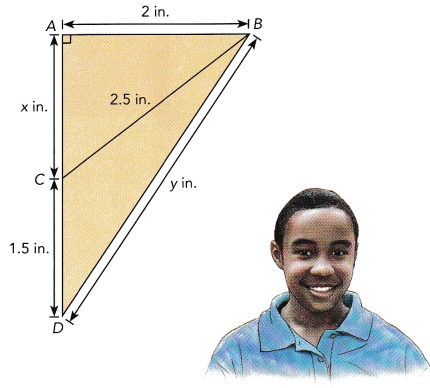
Notice that there are two right triangles.
One has a hypotenuse that is 2.5 inches long, and the other has a hypotenuse that is y inches long.
First find the value of x.

Answer:
The value of x is approximately 2 and
the value of y is approximately 4

Hands-On Activity
Materials
- graph paper
- ruler
Explore Pythagorean Triples
A Pythagorean triple is any set of three whole numbers that satisfy the
Pythagorean Theorem equation c2 = a2 + b2. The table shows several sets of Pythagorean triples.
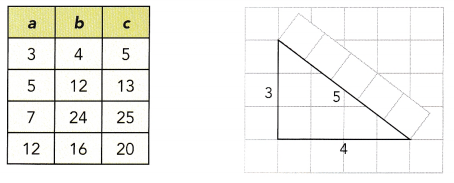
Step 1.
Select one Pythagorean triple from the table. Draw a triangle with legs a units and b units long on a piece of graph paper.
Step 2.
Using a strip of graph paper as a measuring tool, measure the hypotenuse of the triangle. Is it equal to the greatest value in the Pythagorean triple?
Step 3.
Repeat Step 1 and Step 2 using the other Pythagorean triples in the table.
Step 4.
The converse of the Pythagorean Theorem says that if the sum of the squares of the lengths of the two legs of a triangle equals the square of the length of the hypotenuse, then the triangle is a right triangle. Do your triangle measurements support this statement? Explain.
Copy and complete each ![]() with a value and each
with a value and each ![]() with = or ≠.
with = or ≠.
Question 3.
A triangle has side lengths 13 centimeters, 15 centimeters, and 18 centimeter Is it a right triangle?

Answer:
The triangle is a not a right triangle,
Explanation:

Complete.
Question 4.
A ladder 18 feet long is leaning against a wall. The base of the ladder is 9 feet away from the wall. Find the distance from the top of the ladder to the ground. Round your answer to the nearest tenth.
Let the distance from the top of the ladder to the ground be x feet.

The distance from the top of the ladder to the ground is approximately ![]() feet.
feet.
Answer:
The distance from the top of the ladder to the ground is approximately 16 feet,
Explanation:

Complete.
Question 5.
A tree has a shadow length of approximately 9 feet. The distance from the tip of the tree to the tip of the shadow is about 15 feet. How tall is the tree?
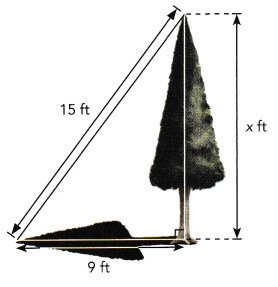
Let the height of the tree be x feet.

Answer:
The height of the tree is 12 feet,
Explanation:

Question 6.
The support pole of the tent shown forms one leg of a right triangle. One side of the tent forms the hypotenuse of the right triangle. Find the length of the base of the tent.
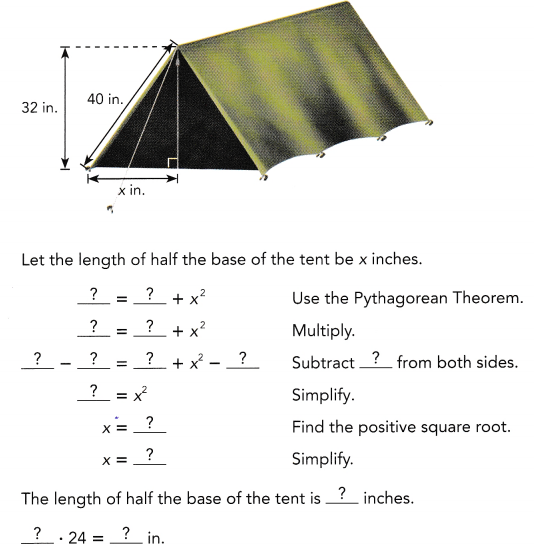
So, the length of the base of the tent is ![]() inches.
inches.
Answer:
The length of the base of the tent is 48 in,
Explanation:

Math in Focus Course 3B Practice 7.1 Answer Key
For this practice, you may use a calculator.
Copy the road signs shown below, identify a right triangle in each sign,
and label the hypotenuse with an arrow.
Question 1.

Answer:

Explanation:
Identified a right triangle in the sign,
and labeled the hypotenuse with an arrow.
Question 2.

Answer:

Explanation:
Identified a right triangle in the sign,
and labeled the hypotenuse with an arrow.
Find the value of x.
Question 3.
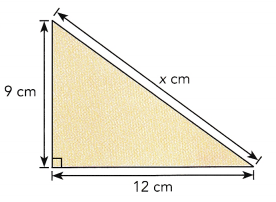
Answer:
x = 15 cm,
Explanation:
Using pythagorean x 2 = 92 + 122 = 81 + 144 =225,
x is equal to square root of 225 which is 15 cm.
Question 4.
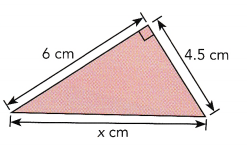
Answer:
x = 3.96 approximately 4 cm,
Explanation:
Using pythagorean x 2 + 4.52 = 62 ,
x 2 + 20.25 = 36,
x 2 = 36 – 20.25 = 15.75,
x is equal to square root of 15.75 which is 3.96 approximately 4 cm.
Question 5.
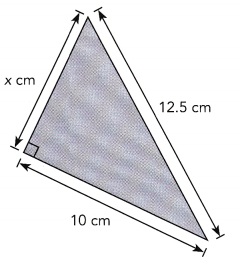
Answer:
4 cm
Explanation:
Using pythagorean x 2 + 102 = 12.52 ,
x 2 + 100 = 156.25,
x 2 = 156.25 – 100 = 15.75,
x is equal to square root of 15.75 which is 3.96 approximately 4 cm.
Question 6.
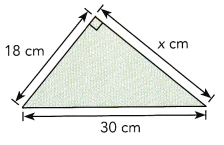
Answer:
Using pythagorean x2 + 4.52 = 62 ,
x 2 + 20.25 = 36,
x 2 = 36 – 20.25 = 15.75,
x is equal to square root of 15.75 which is 3.96 approximately 4 cm.
Calculate each unknown side length. Round your answer to the nearest tenth.
Question 7.
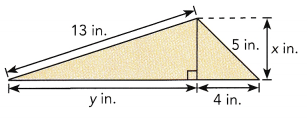
Answer:
x is 3 inches and y is 12.64 approximately 13,
Explanation:
First we calculate the given right angled triangle using
phythagorean theorem x2 + 42 = 52 ,
x2 = 25- 16 = 9 squareroot of 9 is 3 therefore
x is 3 inches, Now
32 + y 2 = 132 ,
y2 = 169- 9 = 160,so y is square root of 160 is 12.64 approximately 13.
Question 8.
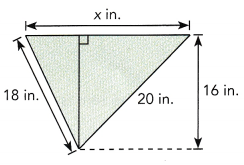
Answer:
the unknown side length is 20 in,
Explanation:
We take x as y +z inches,
First right angle triangle as base z and height 16 in and hypotenuse as 20,
so z2 + 162 = 202,
z2 = 400 – 256 = 144 z is square root of 144 is 12 inches,
Now anthe triangle base y height 16 in and hypotenuse is 18
so y2 + 162 = 182,
y2 = 324- 256 = 68 so y is square root of 68 is 8.24 in,
so x = y + z = 8.24 in + 12 in = 20.24 approximately 20.
Question 9.
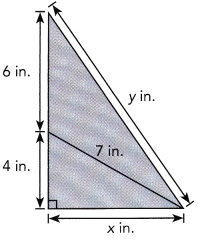
Answer:
x is 6 in and y is 12in,
Explanation:
Given smaller right andle triangle and bigger right traingle,
First smaller using pythogorean theorem
x2 + 42 = 72 ,
x2 = 49-16= 33, x is square root of 33 is 5.744 approximately 6,
Now 102 + 62 = y2 ,
y2 = 100 + 36 = 136, so y is square root of 136 is 11.66 approximately 12,
So x = 6 in and y = 12 in respectively.
Question 10.
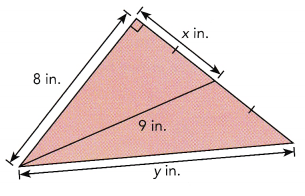
Answer:
x = 4in and y = 9 in,
Explanation:
Given right angled triangle applying pythagorean theorem we have
x2 + 82 = 92,
x2 = 81 – 64 = 17, so square root of 17 is 4.123 approximately 4
x = 4 in and y= 9 in.
Solve. Show your work. Round your answer to the nearest tenth.
Question 11.
Daniel had two pieces of wire. He bent each piece of wire into the shape of a triangle. Determine which triangle is a right triangle.
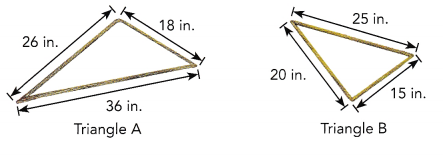
Answer:
Triangle B is a right triangle,
Explanation:
Given Triangle A applying pythagorean theorem
262 + 182 = 362 ,
676 + 324 = 1296,
1000 ≠ 1296,
For Triangle B applying pythagorean theorem
202 + 152 = 252,
400 + 225 = 625,
625 = 625,
The converse of the Pythagorean Theorem says that if the sum of the squares of the lengths of the two legs of a triangle equals the square of the length of the hypotenuse, then the triangle is a right triangle so triangle B is right triangle.
Question 12.
Kendrick wants to build a slide for his son in the backyard. He buys a slide that is 8 feet long. The height of the stairs is 5 feet. Find the distance from the bottom of the stairs to the base of the slide.
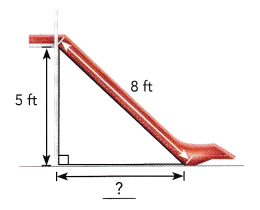
Answer:
The distance from the bottom of the stairs to the base of the slide is
approximately 6 ft,
Explanation:
Given
Kendrick wants to build a slide for his son in the backyard.
He buys a slide that is 8 feet long. The height of the stairs is 5 feet.
To find the distance from the bottom of the stairs to the base b of the slide applying pythagorean theorem as 52 + b2 = 82,
b2 = 64 – 25 = 39, square root of b is 6.244 approximately 6 ft.
Question 13.
Mrs. Hanson uses a wheelchair. Her husband decides to build a ramp to make it easier for her to enter and leave the house. Find the length of the ramp.
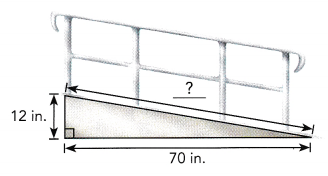
Answer:
The length of the ramp is approximately 71 in,
Explanation:
Given Mrs. Hanson uses a wheelchair. Her husband decides to build a ramp of r inches to make it easier for her to enter and leave the house.
As triangle is right triangle applying pythagorean theorem
r2 = 122 + 702,
r2 = 144 + 4900 =5044, r is square root of 5044 is 71.02 in,
So the length of the ramp is approximately 71 in.
Question 14.
A sign is hung outside a shop on the wall of a building. One end of the brace that holds the sign is connected to the wall. The other end of the brace is connected to the wall by a wire. Use the dimensions in the diagram to find the length of the wire.
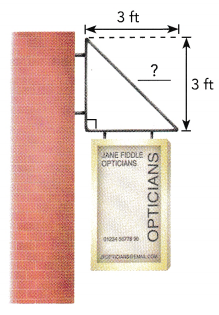
Answer:
The length of wire is approximately 4 ft,
Explanation:
Given a sign is hung outside a shop on the wall of a building.
One end of the brace that holds the sign is connected to the wall.
The other end of the brace is connected to the wall by a wire.
the length l of the wire is l2 = 32 + 32,
l2 = 9 + 9 = 18, l is square root of 18 is 4.24 ,
so the length of wire is approximately 4 ft.
Question 15.
Kelly is flying a kite. When the string, which is 34 feet long, becomes taut, the distance along the ground from the kite to Kelly’s hand is 6.5 feet. Find the vertical height of the kite above her hand.
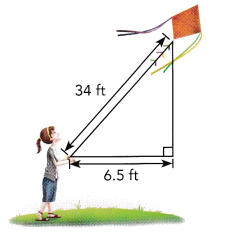
Answer:
Vertical height of the kite above her hand is 33.37 approximately 34 feet,
Explanation:
Given Kelly is flying a kite. When the string, which is 34 feet long,
becomes taut, the distance along the ground from the kite to Kelly’s hand is 6.5 feet.
Let the vertical height v of the kite above her hand. As it is right triangle applying pythogorean theorem
342 = 6.52 + v2,
v2 = 1156 – 42.25 = 1113.75,
so vertical height is square root of 1113.75 is 33.37 approximately 34 feet.
Question 16.
In a movie scene, an actor runs up a ramp that leads from the top of one building to the top of another building. The horizontal distance between the two buildings is 8.6 meters. The height of the shorter building is 18 meters while the height of the taller building is 24 meters. Find the length of the ramp.
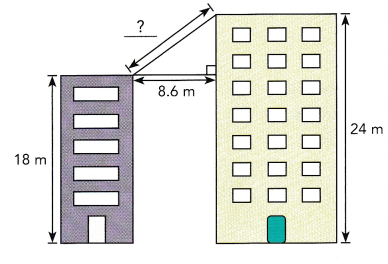
Answer:
The length of ramp is is 6.16 approximately 6 m,
Explanation:
Given in a movie scene, an actor runs up a ramp that leads from the top of one building to the top of another building.
The horizontal distance between the two buildings is 8.6 meters.
The height of the shorter building is 18 meters while the height of the taller building is 24 meters. The length of ramp is l and it is right triangle so
l2 = 8.62 -(24-18)2,
l2 = 73.96 – (6)2,
l2 = 73.96 – 36 = 37.96 , so l is square root of 37.96 is 6.16 approximately 6 m.
Question 17.
The size of a rectangular television screen is given as the length of the diagonal of the screen. Find the size of a television screen that has a height of 38.4 inches and width of 28.8 inches.
Answer:
the length of the diagonal of the screen is 48 inches,
Explanation:
Given the size of a rectangular television screen is given as the length l of the diagonal of the screen.
The size of a television screen that has a height of 38.4 inches and width of 28.8 inches is
l2 = 38.42 + 28.82,
l2 = 1474.56 + 829.44= 2304, l is the square root of 2304 is 48 inches.
Question 18.
A ship sailed from Port X to Port Y. It traveled 20 kilometers due north and then 25 kilometers due west. Find the shortest distance between the two ports.
Answer:
The shortest distance between the two ports is 32.01 approximately 32 kilometers,
Explanation:
Given a ship sailed from Port X to Port Y. It traveled 20 kilometers due north and then 25 kilometers due west. Let s be the shortest distance between the two ports its right triangle applying pythagorean theorem
s2 = 202 + 252
= 400+ 625
= 1025, s is the square root of 1025 is 32.01
approximately 32 kilometers.
Question 19.
Mike wants to build a sailboat. The scale drawing is shown on the right. Find the values of x and y.
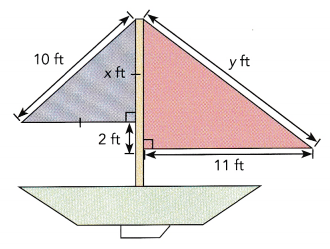
Answer:
The value of x is 7.07 approximately 7 and
y is 14.21 approximately 14,
Explanation:
Given both right traingles 1st triangle applying
pythagorean theorem x2 + x2 = 102,
2x2 = 100,
x2 = 100/2 = 50 so x is square root of 50 is 7.07 approximately 7,
and 2nd triangle applying pythogorean theorem
y2 = 112 +( 7+2)2,
y2 = 121 + 81 = 202, y is squareroot of 202 is 14.21 approximately 14.
Question 20.
The diagonal length of a square window is 40 centimeters. Find the area of the window.
Answer:
The area of window is 800 cm2,
Explanation:

Question 21.
Triangles ABC and ACD are right triangles. AB is 28 meters long. AC is 21 meters long. Find the lengths of \(\overline{B C}\) and \(\overline{A D}\).
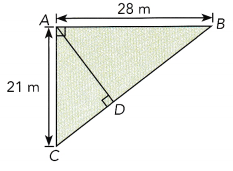
Answer:
Explanation:
Given Triangles ABC and ACD are right triangles. AB is 28 meters long.
AC is 21 meters long.
so BC2 = 212 + 282,
Bc 2 = 441 + 784 = 1225, so Bc is square root of 1225 is 35 m.
Question 22.
The infield of a baseball diamond is a square. Barry measures the distance from home plate to second base and finds that it is about 38.7 meters.
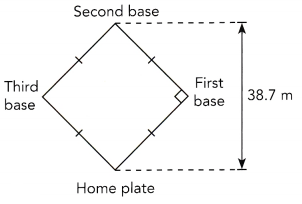
a) Find the approximate distance from home plate to first base.
Answer:
The approximate distance from home plate to first base is 27.4 m
Explanation:
The 38.7 meters is the diagonal of a square; the distance from home plate to first base is a side of the square. The length of the side of the square is the length of the diagonal, divided by the square root of 2.
=38.7/ 1.414 = 27.4 meters.
b) Find the area of the infield.
Answer:
The area of the infield is 750.76 square meters,
Explanation:
Given the side of a baseball diamond is a square and side distance is 27.4 m
so the area of the infield is side × side = 27.4 × 27.4 = 750.76 square meters.
Question 23.
The road sign shown is in the shape of an equilateral triangle. The height of the road sign is 15 inches.
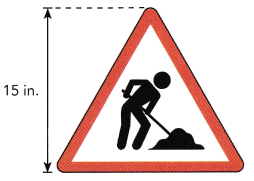
a) Find the length of each side.
Answer:
The length of each side is 17 in,
Explanation:
As we know in an equilateral triangle h = (1/2) × √3 × a.
Angles of Equilateral Triangle: A = B = C = 60° ,
Sides of Equilateral Triangle: a = b = c.
So 15 = 1/2 × √3 × a,
30 = 1.732 × a,
a = 30/1.732 = 17.32 approximately 17 in.
b) Find the area of the sign.
Answer:
The area of the sign is 127.5 in2,
Explanation:
As we know area of triangle is 1/2 × base × height,
1/2 × 17 in × 15 in = 127.5 in2.
Question 24.
Math Journal A salesman selling windows says that a window frame J that is 8 feet long and 6.5 feet wide is rectangular. He also says that it has a diagonal length of 12 feet. Danielle thinks that the salesman is wrong in saying that the window is rectangular. Who is right and why?
Answer:
Yes, Danielle thinks that the salesman is wrong in saying that the window is rectangular,
Explanation:
Given a salesman selling windows says that a window frame J that is 8 feet long and 6.5 feet wide is rectangular.
He also says that it has a diagonal length of 12 feet.
But if we calculate the diagonal length we get
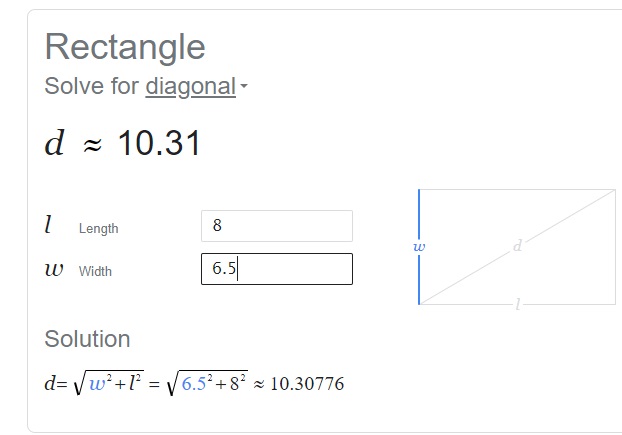
d = 10 not 12 so sales man is wrong.
Question 25.
Math Journal Fiona buys a triangular table. The sides of the table top are 29.4 inches, 39.2 inches, and 49 inches long. She wants to place the table in a corner of a rectangular room. Will the table fit snugly in the corner? Explain.
Answer:
Yes the table fit snugly in the corner,
Explanation:
Given Fiona buys a triangular table.
The sides of the table top are 29.4 inches, 39.2 inches, and 49 inches long.
She wants to place the table in a corner of a rectangular room.
The table fit snugly in the corner.