Go through the Math in Focus Grade 8 Workbook Answer Key Cumulative Review Chapters 1-2 to finish your assignments.
Math in Focus Grade 8 Course 3 A Cumulative Review Chapters 1-2 Answer Key
Concepts and Skills
Write the prime factorization of each number in exponential notation. (Lesson 1.1)
Question 1.
16,807
Answer:
Prime factorization of 16,807 is 7×7×7×7×7×7
The number in the exponential notation is 7⁶.
Question 2.
25,920
Answer:
Prime factorization of 25,920 is 2×2×2×2×2×2×3×3×3×3×5.
The number in the exponential form is 2⁶ × 3⁴ × 5.
Simplify each expression. Write your answer in exponential notation. (Lessons 1.2, 1.3)
Question 3.
\(\frac{\left[\left(\frac{3}{5}\right) \cdot\left(\frac{3}{5}\right)^{3}\right]^{4}}{\left[\left(\frac{3}{5}\right)^{2}\right]^{2}}\)
Answer:
((3/5) • (3/5)³)⁴/((3/5)²)²
⅗ • ( ⅗)³)⁴ • ((⅗)²)²
⅗ • (⅗)¹² • (⅗)⁴
Bases are equal powers should be added.
⅗ • (⅗)¹⁶
(⅗)¹⁷
Question 4.
(a6 • a7)3 ÷ (4a3)2
Answer:
Given (a6 • a7)3 ÷ (4a3)2
(a⁶)³ • (a⁷)³ ÷ (4a)⁶
a¹⁸ • a²¹ ÷ 4a⁶
Bases are equal powers should be added.
a³⁹/4a⁶
¼ × a³⁹/a⁶
¼ × a³³
Simplify each expression. Write your answer using a positive exponent. (Lessons 1.2, 1.3, 1.4, 1.5)
Question 5.
\(\frac{6^{3} \cdot 15^{3}}{\left(7^{0}\right)^{3}}\)
Answer:
6³ • 15³/(7⁰)³
= 90³/7⁰
= 90³/1
= 90³
Question 6.
\(\frac{2^{8} \cdot(-3)^{8} \cdot 3^{0}}{5^{-8}}\)
Answer:
Given 2⁸ • (-3)⁸ • 3⁰/5-8
= -6⁸ • 1/5-8
= -6⁸/5-8
Question 7.
[122 • 32]3 ÷ 36
Answer:
Given [122 • 32]3 ÷ 36
12⁶ • 3⁶ ÷ 3⁶
36⁶/3⁶
12⁶/1⁶
Question 8.
(167 ÷ 164) • \(\frac{\left(5^{0}\right)^{3}}{2^{3} \cdot 4^{3}}\)
Answer:
Given (167 ÷ 164) • (5⁰)³/2³ • 4³
16⁷/16⁴ • 5⁰/2³ • 4³
16³ • 1/2³ • 4³
64³ • (½)³
Question 9.
8-2 • \(\frac{3^{0} \cdot 8^{-3}}{4^{-5}}\) .
Answer:
Given 8-2 • 3⁰ • 8-3/4-5
8-2 • 1 • 8-3/4-5
8-2 • 8-3/4-5
8-5/4-5
2-5/1-5
Question 10.
6-4 • (50)-4 • (\(\frac{1}{3}\))-4 ÷ 3-4
Answer:
6-4 (50)-4 ∙ (\(\frac{1}{3}\))-4 ÷ 3-4 We are given the expression:
6-4 ∙ (50)-4 ∙ (\(\frac{1}{3}\))-4 ÷ 3-4 Simplify:
= 6-4 ∙ \(\frac{1}{3^{-4}} \cdot \frac{1}{3^{-4}}\)
= \(\frac{6^{-4}}{3^{-4}} \cdot \frac{1}{\frac{1}{3^{4}}}\)
= \(\left(\frac{6}{3}\right)^{-4} \cdot 3^{4}\)
= 2-4 ∙ 34
= \(\frac{3^{4}}{2^{4}}\)
= \(\left(\frac{3}{2}\right)^{4}\)
Evaluate the square roots of each number. Round your answer to the nearest tenth when you can. (Lesson 1.6)
Question 11.
576
Answer:
576 = (24)²
Square of 576 is 24
24 rounded to the nearest tenth is 20
Question 12.
1,003.4
Answer:
1,003.4 = (31.6764897046)²
Square of 1,003.4 is 31.6764897046
31.6764897046 rounded to the nearest tenth is 30
Evaluate the cube root of each number. Round your answer to the nearest tenth when you can. (Lesson 1.6)
Question 13.
\(\frac{27}{216}\)
Answer:
27/216
0.125
0.125 = (0.5)³
Cubic root of 27/216 is 0.5
Question 14.
-629.5
Answer:
-629.5 = (-8.57035039349)³
Cubic root of -629.5 is -8.57035039349
Evaluate each expression and write your answer in scientific notation. Identify the greater number. (Lessons 2.1, 2.2, 2.3)
Question 15.
3.27 • 1011 + 3.13 • 1011 and 9.28 • 1011 – 4.15 • 1011
Answer:
3.27 • 1011 + 3.13 • 1011
3.27 + 3.13 • 10¹¹
6.4 • 10¹¹
And 9.28 • 1011 – 4.15 • 1011
9.28 – 4.15 • 10¹¹
5.13 • 10¹¹
6.4 • 10¹¹ is the greater number
Question 16.
9.1 • 10-5 – 8.2 • 10-6 and 1.2 • 10-6 – 5.5 • 10-7
Answer:
9.1 • 10-5 – 8.2 • 10-6
9.1 • 10-5 – 0.82 • 10-5
9.1 – 0.82 • 10-5
8.28 • 10-5
And 1.2 • 10-6 – 5.5 • 10-7
1.2 • 10-6 – 0.55 • 10-6
1.2 – 0.55 • 10-6
0.65 • 10-6
8.28 • 10-5 is the greater number.
Question 17.
8.4 • 105 • 2 • 105 and 3.2 • 10-7 • 2 • 10-5
Answer:
8.4 • 105 • 2 • 105
8.4 • 10⁵ • 2 • 105
16.8 • 10¹⁰
And 3.2 • 10-7 • 2 • 10-5
6.4 • 10-12
16.8 • 10¹⁰ is the greater number.
Question 18.
9.1 • 103 ÷ (7 • 105) and 7.2 • 10-4 ÷ (1.2 • 10-4)
Answer:
9.1 • 103 ÷ (7 • 105)
9.1/7 • 10³/10⁵
1.3 • 1/10²
1.3 • 10-2
And 7.2 • 10-4 ÷ (1.2 • 10-4)
7.2/1.2 • 10-4/10-4
6 • 1
6 = 0.6 • 101
0.6 • 101 is the greater number.
Write each measurement in the appropriate unit in prefix form. (Lesson 2.2)
Question 19.
0.000020 meter
Answer:
0.02 • 103 meter
0.02 millimeter
Question 20.
0.070 gram
Answer:
Given 0.070 gram
0.07 •10-3 gram
Question 21.
35,000,000 bytes
Answer:
Given 35000000 bytes
35 • 10⁶ bytes
0.035 kilobytes
Question 22.
42,000 volts
Answer:
Given 42,000 volts
42 • 10³ volts
42 millivolts.
Problem Solving
Solve. Show your work.
Question 23.
The total surface area of a cube is 4,704 square inches. What is the length of each side? (Chapter 1)
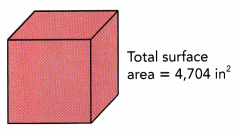
Answer:
From the given question
Total surface area = 4,704 in².
We know that
The total surface area of a cube is 6a²
Where a = side of the cube
6a² = 4704
a² = 4704/6
a² = 784
a = √784
a = 28 in
Question 24.
The volume of a spherical balloon is 12.348π cubic feet. (Chapter 1)
a) Find its radius. Round to the nearest tenth.
Answer:
Given that the volume of a spherical balloon is 12.348π cubic feet.
We know that
The volume of the spherical balloon is 4/3 × πr³
4/3 × πr³ = 12.348π cubic feet.
r³ = 12.348π/4/3× π
r³ = 12.348/ 1.33
r³ = 9.261
r = 2.1
2.1 rounded to the nearest tenth is 2.1
b) Air is pumped into the balloon, so that its radius doubles every 10 seconds. Using 3.14 as an approximation for n, find its surface area after 30 seconds. Round to the nearest tenth.
Answer:
Let r be the radius of the balloon
The radius of the balloon doubles for every 10 seconds.
For 10 seconds radius = r²
For 20 seconds radius = r³
For 30 seconds radius = r⁴
Therefore r⁴ = 30
r = ± 2.340
2.340 rounded to the nearest tenth is 2.3
Question 25.
An oxygen atom has a total of 8 protons. If the mass of one proton is 1.67 • 10-24 gram, find the total mass of the protons in the oxygen atom. Write your answer in scientific notation. Round the coefficient to 3 significant digits. (Chapters 1, 2)
Answer:
Given that the oxygen atom has a total of 8 protons
Mass of one proton = 1.67 • 10-24
Mass of 8 protons = 8
Total mass of a protons = 8 × 1.67 • 10-24
= 13.36• 10-24
13.36• 10-24 Round the coefficient to 3 significant digits is 13.4
Question 26.
The table lists the energy in Calories contained in 100 grams of fruits. (Chapter 2)
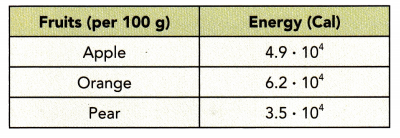
a) Calculate the total energy of the three fruits. Write your answer in scientific notation.
Answer:
Given that the energy in calories contained in 100 grams of apples = 4.9 • 10⁴
The energy in calories contained in 100 grams of oranges = 6.2 • 10⁴
The energy in calories contained in 100 grams of pear = 3.5 • 10⁴
Total energy in all the three fruits = 4.9 • 10⁴ + 6.2 • 10⁴ + 3.5 • 10⁴
= 4.9 + 6.2 + 3.5 • 10⁴
= 14.6 • 10⁴
b) Find the difference in energy contained between 100 grams of apple and 100 grams of pear.
Answer:
Given that the energy in calories contained in 100 grams of apples = 4.9 • 10⁴
The energy in calories contained in 100 grams of pear = 3.5 • 10⁴
Difference = 4.9 • 10⁴ – 3.5 • 10⁴
= 1.4 • 10⁴
The difference in the energy contained between 100 grams of apple and 100 grams of pear is 1.4 • 10⁴
c) How many times more energy does 100 grams .of orange have compared to 100 grams of apple? Round to the nearest tenth.
Answer:
Given that the energy in calories contained in 100 grams of oranges = 6.2 • 10⁴
The energy in calories contained in 100 grams of apples = 4.9 • 10⁴
6.2 • 10⁴ – 4.9 • 10⁴
6.2 – 4.9 • 10⁴
1.3 • 10⁴
The energy in calories contained in 100 grams of oranges is 1.3 • 10⁴ times more than the 100 grams of apple
Question 27.
Jim deposits $2,000 in a bank, which gives 6% interest, compounded yearly. Use the formula A = P (1 + r )n to find the amount of money in his account after 15 years. A represents the final amount of investment, P is the original principal, r is the interest rate, and n is the number of years it was invested. (Chapter 1)
Answer:
Given that
Jim deposits $2,000 in a bank
It gives 6% interest
Using the formula A = P (1 + r )n
P is the original principal
r is the interest rate
n is the number of years
A = 2000(1+6)¹⁵
A = 2000(7)¹⁵
A = 2000 • 7¹⁵