Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 3 Algebraic Linear Equations to finish your assignments.
Math in Focus Grade 8 Course 3 A Chapter 3 Answer Key Algebraic Linear Equations
Math in Focus Grade 8 Chapter 3 Quick Check Answer Key
Explain why each pair of equations is equivalent or not equivalent.
Question 1.
x + 4 = 10 and x – 1 = 3
Answer:
Not equivalent,
Explanation:
Given x + 4 = 10 and x-1 =3 means x = 3+1 =4,
if we substitute x = 4 in x + 4 = 4 + 4 = 8 ≠ 10,
so equations are not equivalent.
Question 2.
\(\frac{1}{5}\)x = 4 and x = 20
Answer:
Equivalent,
Explanation:
Given \(\frac{1}{5}\)x = 4 and x = 20 upon solving
\(\frac{1}{5}\)x = 4 we get x = 4 X 5 = 20 therefore
pair is equivalent as x = 20.
Question 3.
0.5x + 1 = 1.5x and 2x = 2
Answer:
Equivalent,
Explanation:
Given 0.5x +1 = 1.5x and 2x =2 means x= 2/2 equal to 1,
so 0.5 (1) + 1 = 1.5 X 1 is 0.5 +1 = 1.5 , So 1.5 = 1.5,therefore
both equations are equivalent.
Question 4.
2(x + 9) = 14 and 2(x – 7) = -18
Answer:
Equivalent,
Explanation:
Given 2(x -7) = -18 upon solving
2x – 14 = -18,
2x = -18+14,
2x = -4 therfore x = -4/2 = -2 now substituting
2(-2 -7) = – 4 -14 = -18 which is equal to – 18
So both equations are equivalent.
Write a linear equation for each situation. State the independent and dependent variables for each equation.
Question 5.
A manufacturer produces beverages in small and large bottles.
Each small bottle contains s liters of beverages.
Each large bottle contains t liters, which is 1 more liter than the
quantity in the small bottle. Express t in terms of s.
Answer:
t = (s + (sX1)) liters,
Explanation:
Given A manufacturer produces beverages in small and large bottles.
Each small bottle contains s liters of beverages.
Each large bottle contains t liters, which is 1 more liter than the
quantity in the small bottle. Expressing t in terms of s as t = (s + (sX1)) liters.
Question 6.
Hazel is 4 years younger than Alphonso. Express Alphonso’s age, a, in terms of Hazel’s age, h.
Answer:
h=(a-4),
Explanation:
Given Hazel is 4 years younger than Alphonso.
Expressing Alphonso’s age, a, in terms of Hazel’s age, h.
h=(a-4).
Question 7.
A bouquet of lavender costs $12. Find the cost, C, of n bouquets of lavender.
Answer:
C = $12n
Explanation:
Given a bouquet of lavender costs $12, the cost, C, of n bouquets of lavender is
c = $12 X n = $12n.
Question 8.
The distance, d miles, traveled by a bus is 40 times the time,t hours,
used for the journey. Find d in terms of t.
Answer:
d = 40t,
Explanation:
Given the distance, d miles, traveled by a bus is 40 times the time,t hours,
used for the journey is d = 40t.
Solve each equation.
Question 9.
4x = 14 + 2x
Answer:
x =7,
Explanation:
Given 4x = 14 + 2x, upon solving
4x – 2x = 14,
2x = 14,
x = 14/2 = 7.
Question 10.
\(\frac{1}{3}\)v = 2 – \(\frac{2}{9}\)v
Answer:
v = \(\frac{18}{5}\),
Explanation:
Given \(\frac{1}{3}\)v = 2 – \(\frac{2}{9}\)v,
\(\frac{1}{3}\)v = \(\frac{18 -2v}{9}\),
\(\frac{9}{3}\)v = 18 -2v,
3 v = 18 -2v,
5v = 18, therefore v = \(\frac{18}{5}\).
Question 11.
c + 2(1 – c) = 10 – 3c
Answer:
c = 4,
Explanation:
Given c + 2(1 – c) = 10 – 3c,
c + 2 – 2c = 10 -3c,
2 – c = 10 – 3c,
3c-c = 10-2,
2c = 8,
c = 4.
Question 12.
3(2 + 3x) = 13(x + 2)
Answer:
x = -5,
Explanation:
Given 3(2+3x) = 13(x +2) upon solving
6 + 9x = 13x + 26,
6-26 = 13x – 9x,
-20 = 4 x,
x = -5.
Write the decimal for each fraction. Use bar notation.
Question 13.
\(\frac{3}{18}\)
Answer:
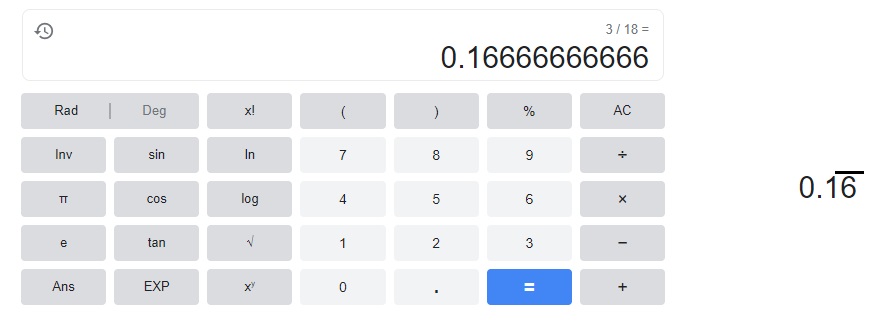
Explanation:
A bar notation, which is a way to show repeating numbers after a decimal point,
here when 3 divides by 18 we get 0.166666 where 6 is repeating so we keep a bar on 6
as shown above.
Question 14.
\(\frac{14}{99}\)
Answer:
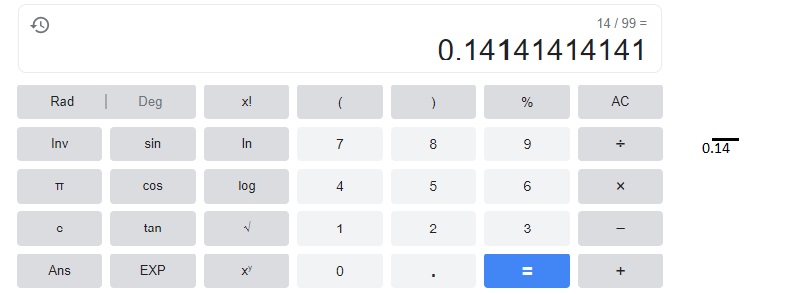
Explanation:
When 14 divides by 99 we get 0.14141414 where 14 is repeating so we keep a bar on 14
as shown above.
Question 15.
\(\frac{13}{12}\)
Answer:
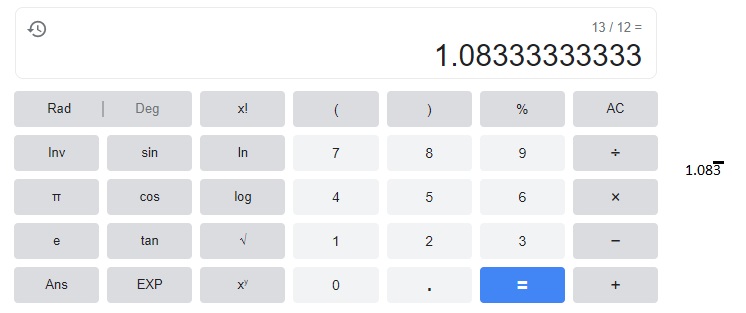
Explanation:
When 13 divides by 12 we get 1.083333 where 3 is repeating so we keep a bar on 3
as shown above.
Question 16.
\(\frac{5}{27}\)
Answer:
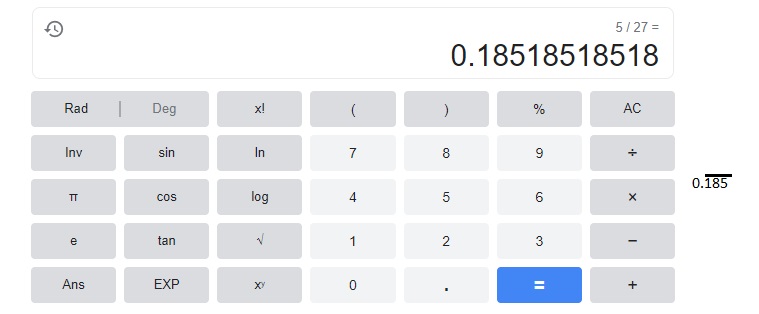
Explanation:
When 5 divides by 27 we get 0.185185 where 185 is repeating so we keep a bar on 185
as shown above.