Math in Focus Grade 8 Chapter 3 Lesson 3.1 Answer Key Solving Linear Equations with One Variable

Math in Focus Grade 7 Course 3 A Chapter 3 Lesson 3.1 Answer Key Solving Linear Equations with One Variable

Math in Focus Grade 8 Chapter 3 Lesson 3.1 Guided Practice Answer Key

Solve each linear equation.

Question 1.

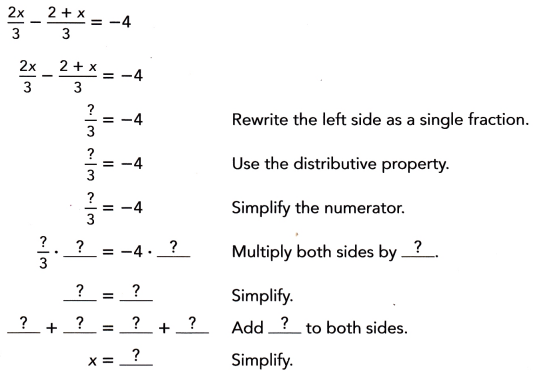
Answer:
x = –\(\frac{2}{15}\)

Explanation:
(2x/3) -(2+x)/3 = -4,
2x/3 -2/3 + x /3 = -4,
(2x/3+ x/3) = -4 +(2/3),
(2x+x)/3 = (-12+ 2)/3,
x = -10/3

Question 2.
00.6(1 – x) + 0.2(x – 5) = 10
Answer:
x = -26

Explanation:
Given 00.6(1 – x) + 0.2(x – 5) = 10 upon solving
0.6 – 0.6x + 0.2 x – (0.2 X 5) = 10,
0.6 – 0.4x -1.0 = 10,
0.6 – o.4x =  11,
-0.4 x = 11 – 0.6,
-0.4x = 10.4
x = -10.4 ÷ 0.4
x = -26

Question 3.
\(\frac{3 x}{5}\) + \(\frac{x-1}{3}\) = \(\frac{2}{15}\)
Answer:
\(\frac{1}{2}\),

Explanation:

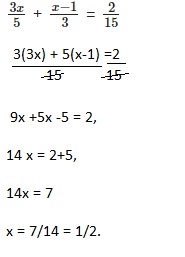
Write each repeating decimal as a fraction. Show your work.

Question 4.
\(0 . \overline{09}\)
Answer:
9/100,

Explanation:

Question 5.
\(0 . \overline{8}\)
Answer:
8/10,

Explanation:

Question 6.
\(0.0 \overline{6}\)
Answer:
6/100,

Explanation:

Write an equation and solve. Show your work.

Question 7.
Mr. Johnson wants to add a circular pond to his backyard. The backyard is 20\(\frac{1}{2}\) yards long, and the pond wilt be
6\(\frac{1}{4}\) yards across. He wants the pond set back from the house, so that the distance from the pond to the back
fence is half the distance from the pond to the back of the house. How far should the pond be from the back of the house?

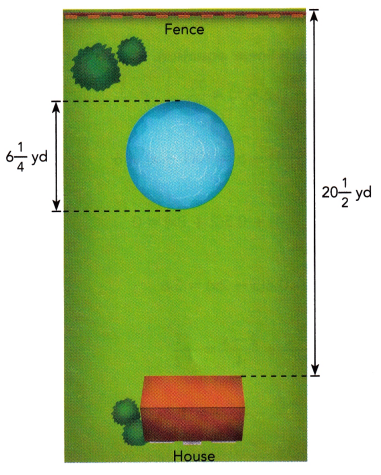
Let the distance from the pond to the house be x yards.
So, the distance from the pond to the fence is \(\frac{1}{2}\)x yards.

The length of the backyard is about yards and the width of the pond is about yards. So the total distance of the pond to the house and of the pond to the gate is around yards. of yards is about yards. So, the answer is reasonable.

Answer:
The distance from the pond to the house is 13.666 yards,

Explanation:
Given let the distance from the pond to the house be x yards.
So, the distance from the pond to the fence is \(\frac{1}{2}\)x yards,

The length of the backyard is about 20 1/2 yards and
the width of the pond is about 6 1/4 yards.
So the total distance of the pond to the house and of the pond to the gate is around 201/2yards.
13.66 yards and 6 1/4  yards is about  20 1/2 yards. So, the answer is reasonable.

Question 8.
A packager of tea leaves blends 3.5 pounds of Tea Leaf A with 1.5 pounds of
Tea Leaf B to make a special blend. One pound of Tea Leaf B costs $2 less than
one pound of Tea Leaf A. The packager finds that the
cost of making the blend is $3 per pound, Find the cost of one pound of Tea Leaf B.
Answer:
$3 is the cost of one pound of tea Leaf B,

Explanation:
Given A packager of tea leaves blends 3.5 pounds of Tea ,
Leaf A with 1.5 pounds of Tea,
Leaf B to make a special blend.
One pound of Tea Leaf B costs $2 less than one pound of Tea Leaf A.
The packager finds that the cost of making the blend is $3 per pound,
So the packager has 3.5 pounds means
Leaf A + Leaf B = 3.5 pound,
1.5 pound + Leaf B = 3.5 Pound,
Leaf B = 2 Pounds to make blend,
Given the packager finds that the cost of making the blend is $3 per pound,
therefore $3 is the cost of one pound of tea Leaf B.

Math in Focus Course 3A Practice 3.1 Answer Key

Solve each linear equation. Show your work.

Question 1.
4x – (10 – x) = \(\frac{15}{2}\)
Answer:
x= 7/2,

Explanation:

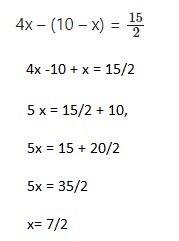
Question 2.
0.5(x + 1) – 1 = 0.2
Answer:
x= 1.4,

Explanation:

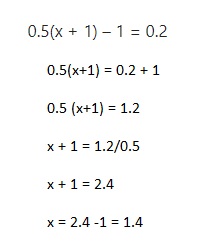
Question 3.
2(x – 1) – 6 = 101(1 – x) + 6
Answer:
x = \(\frac{1}{2}\)

Explanation:
Given 2(x-1)-6 = 101(1-x) + 6,
2x -2 -6 = 101 -101x +6,
2x -8 = 107-101x,
2x +101 x = 107+8,
103 x = 115,
x = 115/103.

Question 4.
8(x – 3) – (x – 3) = 0.7
Answer:
x = 3.1,

Explanation:
Given 8(x – 3) – (x – 3) = 0.7,
8x – 24 – x +3 = 0.7,
7x – 21 = 0.7,
7x = 0.7 + 21,
7x = 21.7,
x = 21.7 ÷ 7,
x = 3.1.

Question 5.
2(x – 4) + 0.5(2 + 8x) = 0
Answer:
x = 7/6,

Explanation:
Given 2(x – 4) + 0.5(2 + 8x) = 0,
2x – 8 + 1.0 + 4x = 0,
6x -7 = 0,
x = 7/6.

Question 6.
5 – 3(x -7 ) = 2(2 – x) – 8
Answer:
x = 30,

Explanation:
Given 5-3(x-7)= 2(2-x)-8,
5 – 3x +21 = 4 -2x -8,
-3x +26 = -2x -4,
26+4 = -2x +3x
30 = x.

Question 7.
3x – 0.4(5 – 2x) = 5.6
Answer:
x = 2,

Explanation:
Given 3x – 0.4(5 – 2x) = 5.6,
3x – 2 + 0.8 x = 5.6,
3x + 0.8 x = 5.6 + 2,
3.8 x = 7.6,
x = 7.6 ÷ 3.8,
x = 2.

Question 8.
6 + \(\frac{1}{3}\)(x – 9) = \(\frac{1}{2}\)(2 – x)
Answer:
x = -12/5,

Explanation:

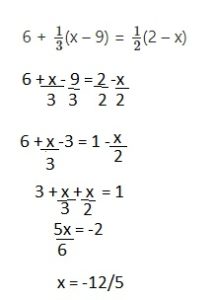
Question 9.
\(\frac{3 x-2}{8}\) + \(\frac{2-x}{4}\) = \(-\frac{1}{2}\)
Answer:
x = -6,

Explanation:

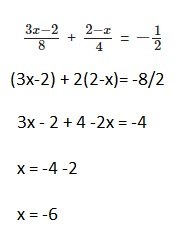
Question 10.
\(-\frac{x+1}{6}\) -\(\) = \(\frac{1}{3}\)
Answer:
x = 3,

Explanation:

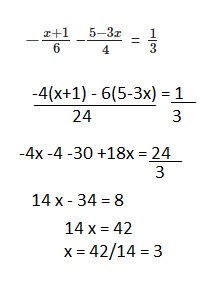
Question 11.
\(\frac{5(x+2)}{3}\) – \(\frac{x-1}{3}\) = 1
Answer:
x = -2,

Explanation:

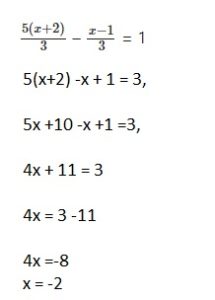
Question 12.
\(\frac{4(2 x+3)}{5}\) – \(\frac{x+1}{4}\) = \(\frac{31}{5}\)
Answer:
x = 3,

Explanation:

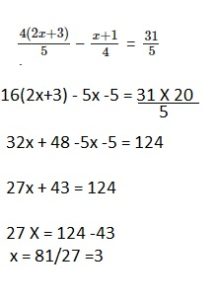
Express each repeating decimal as a fraction. Show your work.

Question 13.
\(0.8 \overline{3}\)
Answer:
5/6,

Explanation:

Question 14.
\(0.0 \overline{8}\)
Answer:
8/99,

Explanation:

Question 15.
\(0 . \overline{1}\)
Answer:
1/9,

Explanation:

Question 16.
\(0.08 \overline{3}\)
Answer:
1/12

Explanation:

Question 17.
\(0.0 \overline{5}\)
Answer:
1/20,

Explanation:

Question 18.
\(0.0 \overline{45}\)
Answer:
9/200,

Explanation:

Solve each problem algebraically. Show your work.

Question 19.
Logan saves $5.50 in dimes and quarters over a week.
He has 20 more dimes than quarters.
Find the number of dimes and quarters he saves.
Answer:
Logan saves 10 quarters and  30 dimes each week,

Explanation:

Question 20.
Maggie makes some fruit punch. She mixes 2\(\frac{1}{2}\) quarts of grape juice with 1\(\frac{1}{2}\) quarts of orange juice. One quart of grape juice costs $1 less than one quart of orange juice. She finds that the total cost of making the fruit punch is $12.50. Calculate the cost of each quart of grape juice and each quart of orange juice.
Answer:
The cost of each quart of orange juice=$3.75,
The cost of each quart of grape juice=$2.75,

Explanation:
The expression for the total cost of making fruit punch is as follows;
Total cost of making fruit punch=
total cost of making grape juice + total cost of making orange juice where;
Total cost of making fruit punch=$12.50,
Total cost of making grape juice=Cost per unit of grape juice×total quantity of grape juice,
Total cost making grape juice=(2 1/2)×g=2.5 g,
Total cost of making orange juice=Cost per unit of orange juice×total quantity of orange juice,
Total cost of making orange juice=(1 1/2)×o=1.5 o,replacing;
12.50=2.5 g+1.5 o…equation 1,
But price per unit of grape juice is one dollars less that the price per unit  of orange juice;
Price per unit of orange juice=o,
Price per unit of grape juice=(o-1), g=o-1
replace the value of g=o-1 in equation 1;
12.50=2.5 g+1.5 o…equation 1
12.50=2.5(o-1)+1.5 o,
12.50=2.5 o-2.5+1.5 o,
2.5 o+1.5 o=12.50+2.50,
4 o=15,
o=15/4=3.75,
g=o-1=3.75-1=2.75,
The cost of each quart of orange juice=o=$3.75,
The cost of each quart of grape juice=g=$2.75.

Question 21.
Ms. Handler walks to work at an average speed of 5 kilometers per hour.
If she increases her speed to 6 kilometers per hour, she will save 10 minutes.

a) Complete the table.

Answer:

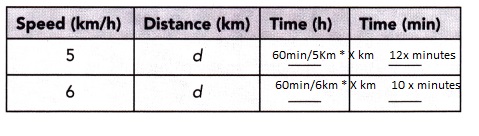
Explanation:
Completed the table as shown above,

b) Find the distance she walks.
Answer:
Ms.Hadler walks 5 km,

Explanation:
I assume that the increase in speed is for the whole distance and
that we want to know far she has to walk.
Let X be the distance,
60min/5Km * X km = 12X minutes,
60min/6km * X km = 10X minutes,
10X +10 = 12X
10 = 2X
X = 5km,

Question 22.
Jane is x years old today. Her brother Kenny is 4 years older.
After seven years, their total combined age will be 24 years.
a) Write a linear equation for their total combined age after 7 years.
Answer:
Linear equation for their total combined age after 7 years is 2x+ 18 =24,

Explanation:
Given Jane is x years old today. Her brother Kenny is 4 years older.,
x and x+4,After seven years, their total combined age will be 24 years,
x +7 +x+4+7 =24,
2x + 18 = 24,
so linear equation for their total combined age after 7 years is 2x +18 = 24.

b) Find Jane’s age today.
Answer:
Janes age today is 3,

Explanation:
Equation is 2x + 18 = 24,
2x = 24-18 = 6,
x = 6/2 = 3 years.

Question 23.
Casper bought some pencils at 50¢ each. He had $3 left after the purchase.
If he wanted to buy the same number of note pads at 80.
Answer:
.50p+3 = .80p-1.50,

Explanation:
.50p+3 = .80p-1.50,
.3p = 4.50,
p = 15,
so, 15 pencils cost $7.50, meaning he started out with $10.50
15 notepads cost $12.00, so he’d be $1.50 short.

Question 24.
Alexis earns 2\(\frac{1}{2}\) times as much as Gary in a day.
James earns $18 more than Gary in a day. If the total daily salary of all three people is $306,
find Alexis’s salary.
Answer:
Alexis salary is $160,

Answer:
Number of shirts sold are 40,

Explanation:
Given a store has y shirts. It sold most of them for $16 each, and the last dozen
were sold on sale for $14 each. If it sold all the shirts for $616,
y=(616-(14 X 12))/16 + 12,
y = (616-168)/16 + 12,
y = 448/16 +12,
y = 28 +12 = 40,
therefore number of shirts sold are 40.

Question 26.
There are 40 questions on a class test. Six points are given for each
correct answer and three points are deducted for each wrong or missing answer.
Find the number of correct answers for a test score of 105.
Answer:
The number of correct answers are 25,

Explanation:
Given there are 40 questions on a class test. Six points are given for each
correct answer and three points are deducted for each wrong or missing answer.
Let x be correct answers incorrect are 40 – x,
so 6x -3(40-x)=105,
6x -120 +3x = 105,
9x= 105+120,
9x = 225,
x = 225 ÷ 9,
x = 25, therefore correct answers are 25 and wrong answers are (40-25)= 15.

Question 27.
Math Journal Georgina was given that the length of a rectangle was
2.5 inches longer than its width, and that the perimeter of the rectangle was 75.4 inches.
She found the length and width algebraically.
How could she use estimation to check if her answers were reasonable?
Answer:
length is 20.1 inches and width is 17.6 inches,

Explanation:
Given Georgina was given that the length of a rectangle was
2.5 inches longer than its width, and that the perimeter of the rectangle was 75.4 inches.
Let length is and width is w so
perimeter = 2(l+w),
75.4 = 2(2.5 +w + w),
75.4 =2(2.5+2w),
37.7 = 2.5 +2w,
2w = 37.7-2.5,
2w = 35.2,
w = 35.2 ÷ 2,
w = 17.6, therfore width is 1
so length = 17.6 + 2.5 = 20.1 inches.

Question 28.
Math Journal Consider the decimal \(0 . \overline{9}\).
a) Find the fraction equivalent of \(0 . \overline{9}\).
Answer:
The fraction eqivalent is 9/10,

Explanation:
0.9 is a decimal fraction, 1 place means tenths,
0.9 is 9/10.

b) The decimal \(0 . \overline{9}\) can be thought of as being equal to the following sum, in which the pattern shown continues forever.
0.9 + 0.09 + 0.009 + 0.0009 + …
How can thinking about this sum help you explain the result you saw in a)?
Answer:
Thinking about this sum helped in explaining the result in tenths place,

Explanation:
Every place value after the decimal point can be expressed as a fraction
with $10$ to some power in the denominator.
The first place after the decimal point is called the “tenths place” If I had $0.9$,
I would have $9$ tenths, or as a fraction $\frac{\mathrm{9/}}{10}$.
The second place after the decimal is called the “hundredths place”.
The question above asks for $0.09$. This would be $9$ hundredths, or as a fraction $\frac{\mathrm{9/}}{\mathrm{100\; and\; so\; on\; thinking\; about\; this\; sum\; helped\; in\; explaining\; the\; result\; in\; tenths\; place.}}$