Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 3 Lesson 3.1 Solving Linear Equations with One Variable to finish your assignments.
Math in Focus Grade 7 Course 3 A Chapter 3 Lesson 3.2 Answer Key Identifying the Number of Solutions to a Linear Equation
Math in Focus Grade 8 Chapter 3 Lesson 3.2 Guided Practice Answer Key
Tell whether each equation is consistent or inconsistent. Justify your answer by simplifying each equation. Write +, ×, or ÷ for each ?
Question 1.
7(x – 3) – 7x – 21 = 0

Answer:
The equation has a solution,
the equation is consistent.
Explanation:
Given 7(x-3)-7x – 21 ≠ 0,
7x – 21 – 7x -21 ≠ 0 (using the distributive property),
-42 ≠ 0 because -42 ≠ 0 the equation has a solution,
the equation is consistent.
Question 2.
\(5\left(x+\frac{1}{5}\right)\) = 5x + 3
Answer:
Inconsistent,
Explanation:
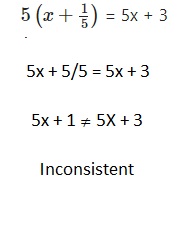
Question 3.
x + \(\frac{1}{4}\) = –\(\frac{1}{4}\)(4x – 1)
Answer:
The equation has a solution,
the equation is consistent.
Equation:
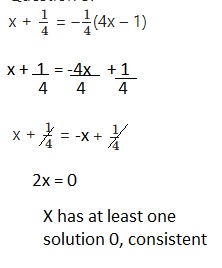
Tell whether each equation is an identity. Justify your answer by simplifying each equation.
Write +, -, ×, or ÷ for each ![]() Write = or ≠ for each
Write = or ≠ for each ![]()
Question 4.

Answer:
Left side is equal to right side,
Equation has an identity,
Explanation:

Question 5.

Answer:
Left side is not equal to right side,
Equation has no identity,
Explanation:

Try substituting some values of x into the equation. If you find that the left side is always equal to the right side, the equation is an identity.

Math in Focus Course 3A Practice 3.2 Answer Key
Tell whether each equation has one solution, no solution, or an infinite number of solutions. Justify your answer.
Question 1.
2x – 3 = -2\(\left(\frac{3}{2}-x\right)\)
Answer:
Equation has one solution,
Explanation:
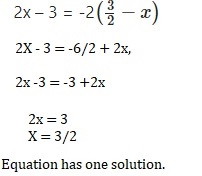
Question 2.
2x + 5 = -4\(\left(\frac{3}{2}-x\right)\)
Answer:
Equation has one solution,
Explanation:
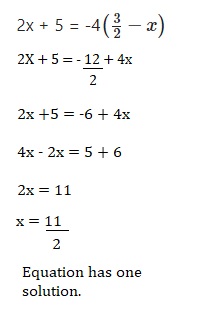
Question 3.
3x + 5 = 2x – 7
Answer:
x = -12, Equation has one solution,
Explanation:
Given 3x + 5 = 2x -7,
3x – 2x = -7 -5,
x = -12,
Equation has one solution.
Question 4.
5y + (86 – y) = 86 + 4y
Answer:
The equation is identity and
an identity equation has infinetly many solutions,
Explanation:
Given 5y + (86 – y) = 86 + 4y upon solving
5y +86 -y = 86 + 4y,
4y + 86 = 86 + 4y ,the equation is identity and
an identity equation has infinetly many solutions.
Question 5.
0.5(6x – 3) = 3(1 + x)
Answer:
No solution,
Explanation:
Given 0.5(6x -3) = 3(1 + x),
(0.5 X 6x) – (0.5 X 3) = 3 +3x,
3x -1.5 = 3 + 3x
-1.5 ≠ 3, So the equation has no solution,
Question 6.
4(18a — 7) + 40 = 3(4 + 24a)
Answer:
The equation is identity and
an identity equation has infinetly many solutions,
Explanation:
4 X 18a – 4 X 7 + 40 = 12 + 72a
72 a – 28 +40 = 72a+ 12
72a + 12 = 72a+12,
both are equal so infinite solutions.
Question 7.
\(\frac{1}{7}\)(7x – 21) = 8x + 7x – 24
Answer:
Equation has one solution,
Explanation:
Given \(\frac{1}{7}\)(7x – 21) = 8x + 7x – 24,
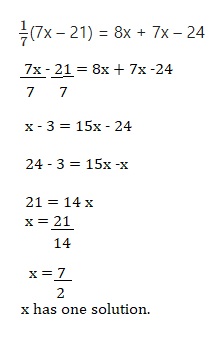
Question 8.
\(\frac{1}{6}\)(12x – 18) = 2\(\left(x-\frac{3}{2}\right)\)
Answer:
The equation is identity and
an identity equation has infinetly many solutions,
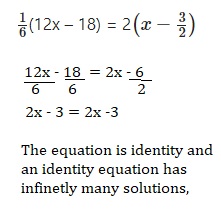
Question 9.
7 – 0.75x = -7\(\left(\frac{3}{28} x+1\right)\)
Answer:
No solution,
Explanation:
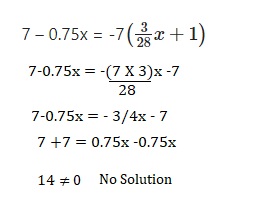
Question 10.
6 + 0.5y = -2\(\left(3-\frac{1}{4} y\right)\)
Answer:
No solution,
Explanation:
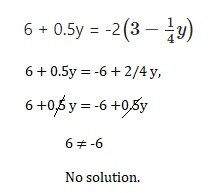
Question 11.
\(\frac{x-3}{4}\) = 0.25x – 0.75
Answer:
The equation is identity and
an identity equation has infinetly many solutions,
Explanation:
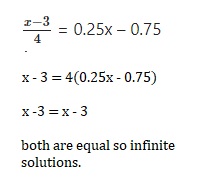
Question 12.
\(\frac{1}{3}\)x + 5 = \(\frac{1}{6}\)(2x – 5)
Answer:
No solution,
Explanation:
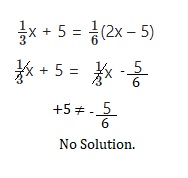
Solve. Show your work.
Question 13.
Cabinet A is 5 inches taller than Cabinet B. Cabinet C is 3 inches taller than Cabinet B whose height is x inches.
a) Write algebraic expressions for the heights of cabinets A and C.
Answer:
Cabinet A = 5 + x,
Cabinet C = 3 + x,
Explanation:
Given Cabinet B height is x inches as Cabinet A is 5 inches taller than Cabinet B
Cabinet A = 5 + x and Cabinet C is 3 inches taller than Cabinet B so Cabinet C = 3 + x.
b) If the total height of the three cabinets is (3x + 8) inches, can you solve for the height of Cabinet B? Explain.
Answer:
We cannot solve for the height of Cabinet B
we need numbers.
Explanation:
Given the total height of the three cabinets is (3x + 8) inches,
we have Cabinet A = 5 + x, Cabinet B = x and Cabinet C = 3 + x,
5 + x + x +3 + x = 3x +8, We cannot solve for the height of Cabinet B
we need numbers.
Question 14.
A room’s floor is y meters long. Its width is 5 meters shorter.
If the perimeter of the floor is (4y + 1) meters, can you solve for its length? Explain.
Answer:
There is not answer. Or, the problem needs more definition,
Explanation:
Room Floor Length(L) = y m.Width(W) y – 5 m.
Perimeter = 4y + 1,Find: Length(L),
Using perimeter formula P = 2L + 2W to get an equation to solve.
P = 4y + 1 = 2(y) + 2(y – 5),
4y + 1 = 2y + 2y – 10 => 1 = -10,
There is not answer. Or, the problem needs more definition.
Question 15.
Math Journal
Grace gave her sister a riddle: I have a number x. I add 15 to twice x to get result A.
I subtract 4 from x to get result B. I multiply result B by 3 to get result C.
Result A is equal to result C. Grace’s sister said the riddle cannot be solved,
but Grace thought otherwise. Who is right? Explain.
Answer:
Grace is right she solved the riddle,
Explanation:
Given Grace gave her sister a riddle: I have a number x. I add 15 to twice x to get result A.
A= 15 + 2x, I subtract 4 from x to get result B. B = x -4,
I multiply result B by 3 to get result C. 3B = C ,
Result A is equal to result C, 15 + 2x = C = 3(x-4)
15 + 2x = 3x – 12,
15 + 12 = 3x -2x,
27 = x.
Grace is right she solved the riddle.
Question 16.
Math Journal Look at this “proof” that 2 = 0.

What is wrong with this proof? How can a true statement lead to an inconsistent equation?
Answer:
Substituting values of a and b and a true statement lead to an inconsistent equation,
Inconsistent equations is defined as two or more equations that are
impossible to solve based on using one set of values for the variables.
Explanation:
As when a =1 and b= 1 then (a-b)(a+b) = 0 means
(1-1)(1+1) = 0,0=0 true statement,
0= 0 but if (a-b)(a+b) =0 dividing both sides by (a-b) we get
a + b = 0 substitute for a and b we get 1 + 1 = 0 and 2 = 0 which is inconsistent.