Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 3 Lesson 3.3 Understanding Linear Equations with Two Variables to finish your assignments.
Math in Focus Grade 7 Course 3 A Chapter 3 Lesson 3.3 Answer Key Understanding Linear Equations with Two Variables
Math in Focus Grade 8 Chapter 3 Lesson 3.3 Guided Practice Answer Key
Complete.
Question 1.
Write a linear equation for the relationship between days, d, and weeks, w. A week has ![]() days. So a linear equation for d in terms of w is
days. So a linear equation for d in terms of w is ![]() .
.
Answer:
Linear equation between days and weeek is
d= 7w,
Explanation:
Assuming there are 7 days in a week, W weeks will have 7 X W days,
So d = 7w.
Question 2.
George rented a car from a company for a week. The table shows the rental charges.

Answer:
A linear equation for C in terms of d is c = 100+(0.1 X d),
Explanation:

Technology Activity
Materials:
- graphing calculator
Use A Graphing Calculator To create Tables Of Values For Linear Equations With Two Variables
Work individually or in pairs.
You can use a graphing calculator to create tables of values for linear equations with two variables. Use the steps to create a table of values for the equation y = \(\frac{x}{\pi}\). This will give you the diameter y of a circle when you substitute a given circumference x.
Step 1.
Enter the equation using the equation screen.
Step 2.
Set the table function to use values of x starting at 0, with increments of 1.
Step 3.
Display the table. It will be in two columns as shown.

Step 4.
Repeat Step 1 to Step 2 for the equation y = -2x + \(\sqrt{2}\).
Find the value of y when x = -4
Answer:
9.414,
Explanantion:
When x =-4, y = -2x + \(\sqrt{2}\),
y = -2(-4) + 1.414
y= 8+ 1.414,
y = 9.414.
Question 3.
y = 7 + 3x
Answer:
y= -5,
Explanation:
Given y = 7 +3x,
y= 7 +3(-4),
y= 7 – 12,
y= -5.
Question 4.
\(\frac{1}{3} y\) = 2\(\left(x-\frac{1}{6}\right)\)
Answer:
y = -25
Explanation:
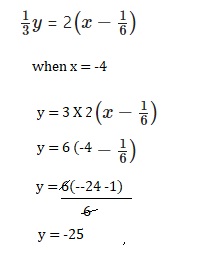
Question 5.
-6x – y = 17.75
Answer:
y = -41.75,
Explanation:
Given -6x – y = 17.75 when x =- 4
-6(-4)-y = 17.75,
-24 -17.75 = y
y = – 41.75.
Create a table of x- and y-values for each equation. Use integer values of x from 1 to 3.
Question 6.
2y = 1.2x + 1
Answer:
When x =1, y= 1.1, x= 2 , y = 1.7 and when x = 3, y is 2.3,
Explanation:
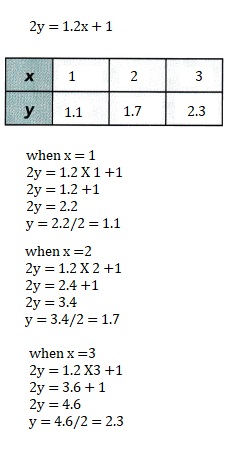
Question 7.
4y – 11x = 6
Answer:
When x =1, y = 17/4 or 4.25,
x= 2, y = 7 and x =3, y = 39/4 or 9.75,
Explanation:
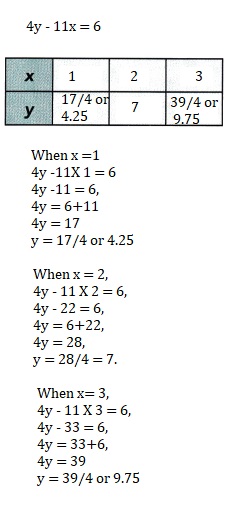
Complete the table of x- and y-values for each equation.
Question 8.
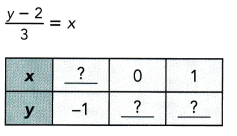
Answer:
When y =-1 x is -1,
when x = 0 y is 2 and
when x =1 y is 5,
Explanation:
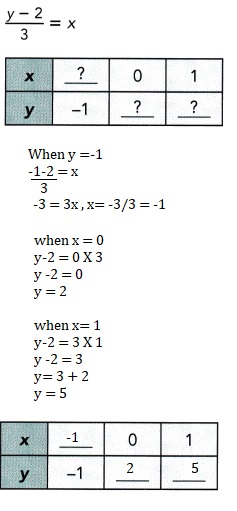
Question 9.
3(x + 1) – 2y = 0
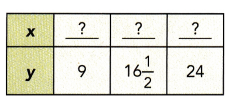
Answer:
y = 9, x is 5, when y =16 1/2, x is 10 and
y = 24, x = 15,
Explanation:

Math in Focus Course 3A Practice 3.3 Answer Key
Write a linear equation for the relationship between the given quantities.
Question 1.
meters, m, and centimeters, c
Answer:
1 m = 100 c
Explanation:
As 1 meter is equal to 100 centimeters so
1 m = 100 c.
Question 2.
hours, h, and seconds, s
Answer:
1 h= 3600 s,
Explanation:
As 1 hour is equal to 3600 seconds so
1h = 3600 s.
Question 3.
feet, f, and inches, i
Answer:
1 f= 12 i,
Explanation:
As 1 foot is equal to 12 inches so
1f = 12 i.
Question 4.
dollars, d, and cents, c
Answer:
1 d = 100 c
Explanation:
As 1 dollar is equal to 100 cents so
1 d = 100 c.
Find the value of y when x = 2.
Question 5.
2x – 1 = y + 4
Answer:
y = -1,
Explanation:
Given 2x -1 = y+4, substituting x =2 we get
2 X 2 -1 = y +4,
4 -1 = y +4,
3 = y + 4,
y = 3 – 4 = -1.
Question 6.
y = \(\frac{1}{7}\)(x + 5)
Answer:
y = 1,
Explanation:
Given y = \(\frac{1}{7}\)(x + 5) and x =2
y = \(\frac{1}{7}\)(2 + 5)= \(\frac{1}{7}\)(7) = 1.
Question 7.
3x – 11 = 2(y – 4)
Answer:
y = 3/2 or \(\frac{3}{2}\),
Explanation:
Given 3x – 11= 2(y-4),
3 X 2 – 11 = 2y – 8,
6 -11 +8 = 2y,
14 – 11 = 2y
3=2y,
y = 3/2.
Question 8.
4y = 5(x – 1)
Answer:
y = 5/4 or \(\frac{5}{4}\),
Explanation:
Given 4y=5(x-1) and x =2,
4y =5(2-1),
4y = 5(1),
4y = 5,
y = 5/4.
Find the value of x when y = -7.
Question 9.
2(3x – 7) = 9y
Answer:
x = -49/6 or –\(\frac{49}{6}\),
Explanation:
Given 2(3x-7) = 9y and y =-7,
6x – 14 = 9 X -7,
6x – 14 = -63,
6x = -63 +14
6x = -49
x= -49/6.
Question 10.
\(\frac{2 x-1}{5}\) = 2(y + 7)
Answer:
x = 1/2,
Explanation:
Given \(\frac{2 x-1}{5}\) = 2(y + 7) when y =-7,
2x -1 = 10(-7+7),
2x – 1 = 0,
2x = 1,
x= 1/2.
Question 11.
2x + y = 0.1(y + 3)
Answer:
x= 3.3,
Explanation:
Given 2x+y =0.1(y +3) when y=-7,
2x – 7 = 0.1(-7+3),
2x – 7 = 0.1(-4),
2x -7 = -0.4,
2x = -0.4 + 7,
2x = 6.6,
x= 6.6/2 = 3.3.
Question 12.
2y – 5x = 26
Answer:
y = -9/2 or \(\frac{-9}{2}\),
Explanation:
Given 2y – 5x = 26, when x = -7,
2y -5(-7)= 26,
2y + 35 = 26,
2y = 26-35,
2y=-9
y = -9/2.
Create a table of x- and y-values for each equation. Use integer values of x from 1 to 3.
Question 13.
y = \(\frac{1}{4}(8-x)\)
Answer:
x = 1, y = 7/4, x=2, y =3/2 and
when x = 3 y = 5/4,
Explanation:

Question 14.
x + 7 = \(\frac{1}{2}(y-5)\)
Answer:
x=1, y = 21,
x=2, y = 23,
x = 3, y =25,
Explanation:

Question 15.
-4y = 2x + 5
Answer:
x = 1, y = -7/4,
x = 2, y =-9/4,
x= 3, y = -11/4,
Explanation:
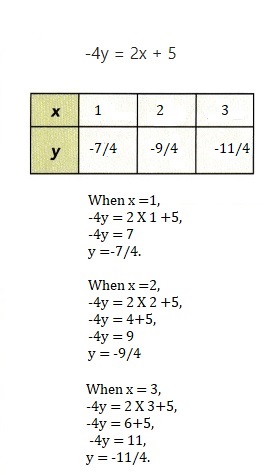
Question 16.
\(\frac{1}{2}(x+4)\) = \(\frac{1}{3}(y+1)\)
Answer:
x=1, y = 13/2,
x= 2, y =8,
x =3 then y = 19/2,
Explanation:
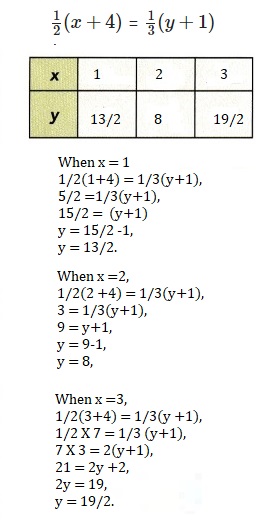
Complete the table of x- and y-values for each equation.
Question 17.
y = 5(x + 3)
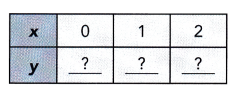
Answer:
x= 0, y =15, x= 1, y = 20, x = 2 , y =25,
Explanation:
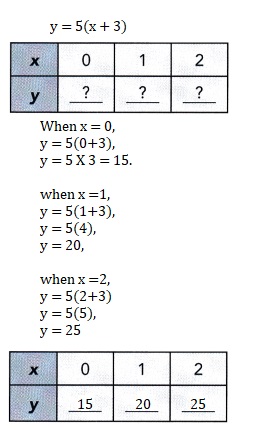
Question 18.
\(\frac{x}{4}\) + y = 1
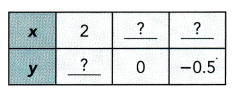
Answer:
x = 2, y = 1/2 or 0.5,
y =0, x = 4 and
when y = -0.5, x = 6,
Explanation:
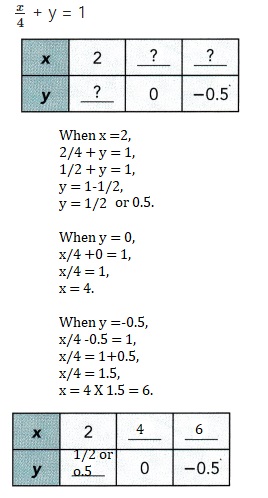
Question 19.
3x – 4y = \(\frac{5}{3}\)
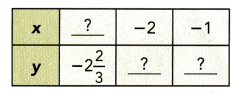
Answer:
y =-2 2/3, x =-3,
x=-2, y =-23/12 and
x = -1 , y = -7/6,
Explanation:

Question 20.
5(y + 4) = 8x
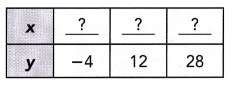
Answer:
y = -4, x = 0, y = 12 , x = 10 and when y = 28 , x is 20,
Explanation:
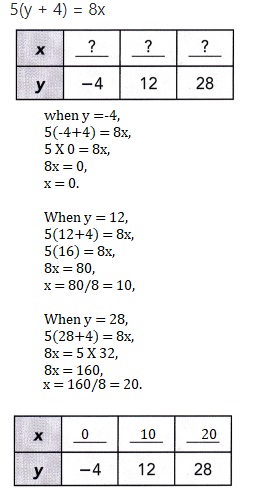
Solve. Show your work.
Question 21.
A research student recorded the distance traveled by a car for every gallon of gasoline used.
She recorded the results in the following table.
Write a linear equation for the distance traveled,
d miles, in terms of the amount of gasoline used, g gallons.

Answer:
d=40.5g,
Explanation:
Given a research student recorded the distance traveled by a car for every gallon of gasoline used.
She recorded the results in the following table. For amount of Gasoline used (g gallons)
for 1 gallons it is 40.5 miles, for 2 gallons it is 2 X 40.5 = 81 miles,
for 3 gallons it is 3 X 40.5 = 121.5 miles and for 4 gallons it is 4 X 40.5 = 162 miles it is
linear so the equation is d = 40.5 g respectively.
Question 22.
Mr. Taransky sells blood pressure monitors. He earns a monthly salary
that includes a basic amount of $750 and $5 for each monitor sold.
a) Write a linear equation for his monthly salary, M dollars, in terms of the number of monitors sold, n.
Answer:
M= $750 +$5n,
Explanation:
Given Mr. Taransky sells blood pressure monitors. He earns a monthly salary
that includes a basic amount of $750 and $5 for each monitor sold.
Writing a linear equation for his monthly salary, M dollars, in terms of the number of monitors sold, n.
M = $750 +$5n.
b) Use the equation to complete the table of values below.

Answer:
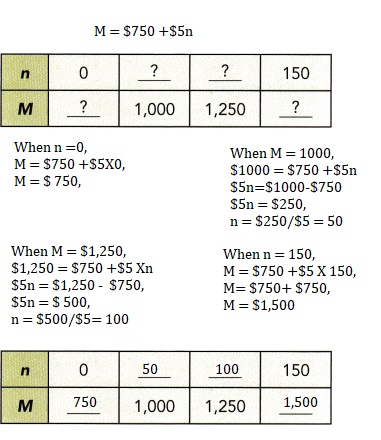
Explanation:
Completed the table as shown above.
c) Calculate his salary when he sold 300 monitors in a month.
Answer:
Mr. Taransky salaray is $2,250 when he sold 300 monitors in a month,
Explanation:
Given to calculate his salary when he sold 300 monitors in a month,
M = $750 +$5 X 300,
M = $750 + $1,500 = $2,250.
d) His salary was $1,450 in January. How many monitors did he sell that month?
Answer:
140 monitors,
Explanation:
Given his salary was $1,450 in January, Monitors did he sell that month is
$1,450 = $750+$5n,
$5n = $1450-$750,
$5n = $700,
n = 700/5 = 140 monitors.
Question 23.
Bernadette’s cell phone plan costs a basic charge of $20 a month plus
5c per minute of calling time after she uses the first 300 minutes of calling time in a month.
a) Write a linear equation for the total cost, C dollars, in terms of the total
number of minutes of calling time, t minutes.
Answer:
Linear equation is c = 20 + 0.05(t -300),
Explanation:
Given Bernadette’s cell phone plan costs a basic charge of $20 a month plus
5c per minute of calling time after she uses the first 300 minutes of calling time in a month.
The linear equation for the total cost, C dollars, in terms of the total
number of minutes of calling time, t minutes is c = 20 + 0.05(t -300).
b) Create a table of t- and C-values for the linear equation. Use t = 300, 400, and 500.
Answer:
When t = 300, c = 20, t=400 c = 25 and when t = 500 c is 30,
Explanation:

c) Find the total number of minutes of calling time Bernardette uses in a month when her bill is $32.
Answer:
540 minutes,
Explanation:
As we have c =20+0.05(t-300) the total number of minutes of calling time
Bernardette uses in a month when her bill is $32
$32 = 20 +0.05(t-300),
$32 – $20 = 0.05 (t-300),
$12 = 0.05(t -300)
t – 300 = 12/0.05 = 240
t = 240 +300 = 540 minutes.
Question 24.
A parking lot charges $1.50 for the first hour or part of an hour. After the first hour, parking costs 70¢ for each half hour, or part of a half hour. Mr. Fischer parked his car in the parking lot for t hours.
a) Write a linear equation for the total cost of parking, y dollars, in terms of t.
Answer:
y= $1.50 + 2(0.7)(t-1)
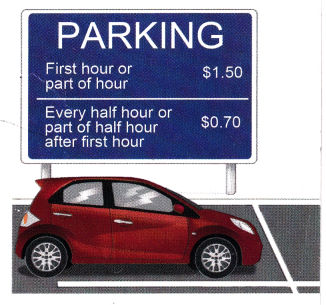
Explanation:
Given a parking lot charges $1.50 for the first hour or part of an hour.
After the first hour, parking costs 70¢ for each half hour, or part of a half hour.
Mr. Fischer parked his car in the parking lot for t hours.
linear equation for the total cost of parking, y dollars, in terms of t.
y = $1.50 +2(0.7)(t-1).
b) Find the amount Mr. Fischer had to pay if he parked his car for a 40 minutes.
Answer:
Mr. Fischer has to pay $1.50,
Explanation:
Given the amount Mr. Fischer had to pay if he parked his car for a 40 minutes as
t hours is less than 1 hour, we take t as 1,
Mr.Fischer has to pay y= $1.50 +2(0.7)(1-1),
y= $1.50 + 0
y = $1.50.
c) What was the total cost if he parked for 1 hour and 40 minutes?
Answer:
The total cost if he parked for 1 hour and 40 minutes is $2.90,
Explanation:
Given the parked time is 1 hour and 40 minutes more than an
hour and half hour so we take t as 2,
y = $1.50+2(0.7)(2-1) = $1.50 + 2 X 0.7,
y= $1.50 +$1.40 = $2.90.