Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 8 Review Test to score better marks in the exam.
Math in Focus Grade 8 Course 3 B Chapter 8 Review Test Answer Key
Concepts and Skills
State whether a rotation, translation, or a combination of both is involved in each activity.
Question 1.
A turning blade of a windmill
Answer:
A turning blade of a windmill is rotation. Because the blade of a windmill rotates in a horizontal axis.
Question 2.
Pressing the keys on a computer keyboard
Answer:
Pressing the keys on a computer keyboard is a translation. Because the keyboard translates the number into binary data.
Question 3.
A printer head moving left and right
Answer:
A printer head moving left and right is a translation. Because it is moving from left to right and right to left it means translating from left to right and right to left.
Question 4.
Wheels on a moving bicycle
Answer:
Wheels on a moving bicycle is a rotation. Because the bicycle wheel is rotated in clockwise and anticlockwise.
Describe the translations.
Question 5.
Climbing up 8 steps of a staircase (assume horizontal and vertical distances of each step are the same)
Answer:
The translation is a type of transformation that moves each point in a figure with the same distance in the same direction. Climbing up 8 steps of a staircase is a translation.
Question 6.
Taking an elevator from level 2 to level 5 of a building
Answer: Taking an elevator from level 2 to level 5 of a building is translation. Because the elevator is a device that moves up and down.
Write an equation of the line(s) of reflection.
Question 7.
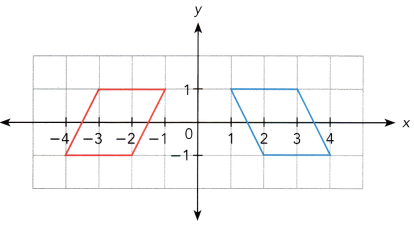
Answer:
Reflection in x axis is (x,y) = (x,-y)
Reflection in y axis is (x,y) = (-x,y)
In the above figure consider the left image as ABCD and right image as PQRS
The reflection in y axis is
P(1,1) reflection is A(-1,1)
Q(3,1) reflection is B(-3,1)
R(4,-1) reflection is C(-4,-1)
S(2,-1) reflection is D(-2,-1)
Question 8.
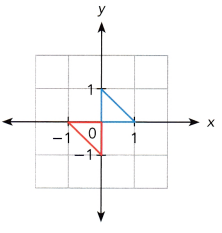
Answer:
Reflection in x axis is (x,y) = (x,-y)
Reflection in y axis is (x,y) = (-x,y)
Consider the image below the x axis is OAB and above the x axis is OPQ
O(0,0) reflection is O(0,0)
A(0,-1) reflection in x axis is P(0,-(-1)) = P(0,1)
B(-1,0) reflection in y axis is Q(-(-1),0) = B(1,0)
Question 9.
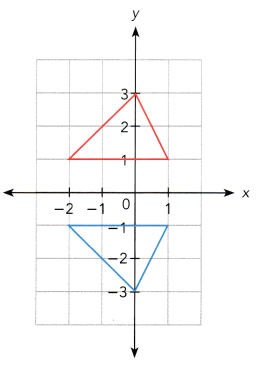
Answer:
Reflection in x axis is (x,y) = (x,-y)
Reflection in y axis is (x,y) = (-x,y)
Consider the image below the x axis is ABC and above the x axis is PQR
A(1,1) reflection to x axis is P(1,-1)
B(0,3) reflection to x axis is Q(0,-3)
C(-2,1) reflection to x axis is R(-2,-1)
Question 10.
Answer:
Each diagram shows a figure and its line of reflection. On a copy of the graph, draw the image.
Question 11.
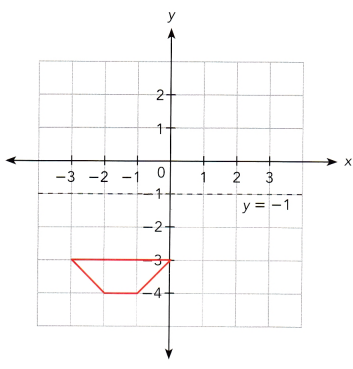
Answer:
Reflection in x axis is (x,y) = (x,-y)
Reflection in y axis is (x,y) = (-x,y)
Consider the image below the x axis is ABCD.
A(-3,-3) reflection to the x axis is (-3,3)
B(0,-3) reflection to the x axis is (0,3)
C(-1,-4) reflection to the x axis is (-1,4)
D(-2,-4) reflection to the x axis is (-2,4)
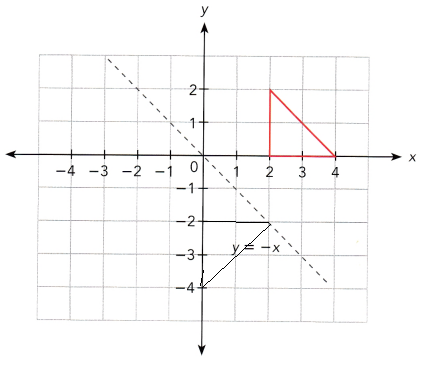
Question 12.
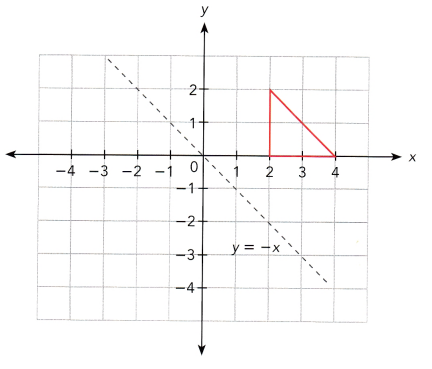
Answer:
Solve on graph paper. Show your work.
Question 13.
\(\overline{\mathrm{AB}}\) is dilated with center at the origin and scale factor 2. Draw \(\overline{\mathrm{AB}}\) and its image \(\overline{A^{\prime} B^{\prime}}\). Use 1 grid square on the horizontal axis to represent 1 unit for x interval from -4 to 10, and 1 grid square on the vertical axis to represent 1 unit for the y interval from -2 to 4.
a) A (2, 1) and B (5, 2)
Answer:
b) A (1, -1) and B (-2, 2)
Answer:
Question 14.
The table shows the coordinates for ∆XYZ and its images using two transformation. Use 1 grid square on both axes to represent 1 unit for the interval from -3 to 9.

a) ∆XYZ is mapped onto ∆X’Y’Z’ and ∆X”Y”Z” by a dilation. Draw each triangle and its image on the same coordinate plane. Then mark and label D as the center of dilation.
Answer:
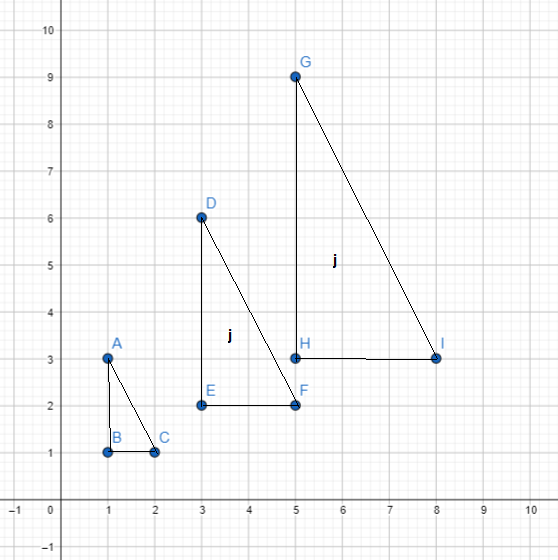
In the drawn graph ABC = XYZ, DEF = X’Y’Z’, GHI = X”Y”Z”
b) ∆XYZ is mapped onto ∆ABC by a rotation 90° counterclockwise about the origin. Draw ∆ABC on the coordinate plane.
Answer:
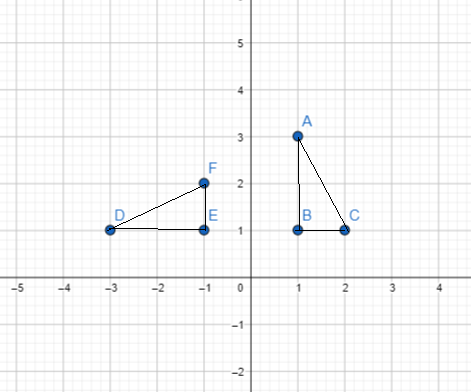
In the drawn map XYZ = ABC and ABC = DEF
90⁰ counterclockwise rotation = (-y,x)
X(1,3) = X(-3,1)
Y(1,1) = Y(-1,1)
Z(2,1) = Z(-1,2)
c) ∆XYZ is mapped onto ∆PQR by a translation 3 units to the left and 4 units up. Draw ∆PQR on the coordinate plane.
Answer:
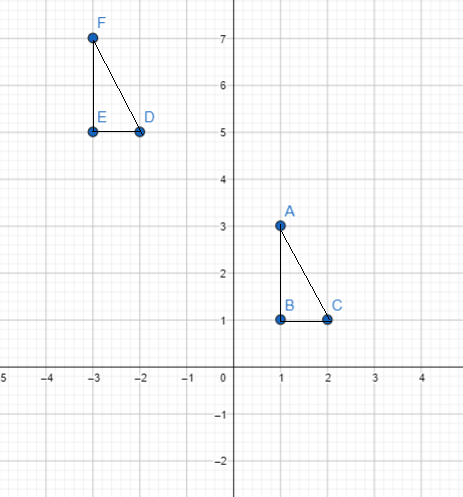
In the drawn graph XYZ = ABC and PQR = DEF.
In the graph ∆DEF is the translation.
d) Compare the transformations that mapped ∆XYZ onto ∆ABC and ∆PQR in terms of preservation of the shape and size of ∆XYZ.
Answer:
The transformations ∆XYZ onto ∆ABC is rotation it means the figure turns in the clockwise or counter clockwise but it doesn’t change the shape and size.∆PQR onto ∆XYZ is a translation it means moving the figure on the coordinate plane without changing the shape and size.
Problem Solving
Solve. Show your work.
Question 15.
Jane had lunch with her friends from 1 P.M. to 2 P.M. Describe the geometric transformation of the hour hand of the clock.
Answer:
Question 16.
A scientist used a sensor to track the movement of a mouse. It moved from the point (-2, 3) to the point (8, 6). State the new coordinates of any point (x, y) under this translation.
Answer:
Given that,
The mouse moved from the point (-2,3) to the point (8,6)
(x1,y1) = (-2,3)
(x2,y2) = (8,6)
New coordinates are (x,y)
x coordinate = x2 – x1 = 8 – (-2) = 8 + 2 = 10.
y coordinate = y2 – y1 = (6-3) = 3.
Therefore, New coordinates are (x+10, y+3).
Question 17.
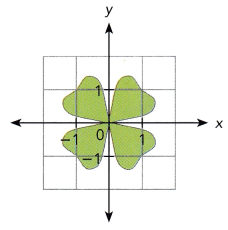
Mrs. Morales outlined a clover with four identical leaflets, as shown, on a coordinate plane. The center of the clover is at (1, 0).
a) How many lines of symmetry does the clover have? Sketch them on a copy of the clover leaf.
Answer:
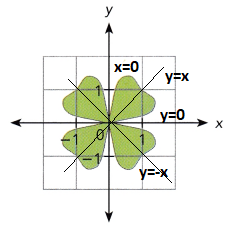
b) Find an equation of each line of reflection.
Answer:
The equation of each line of reflection is x = 0, y = 0, y = -x and y = x
Therefore there are four symmetry.
Question 18.
A circular mold in a Petri dish had a diameter of \(\frac{1}{2}\) inch. The diameter grew by 32% in a day.
a) What is the scale factor of dilation?
Answer:
Given that the circular in a Petri dish has a diameter of ½ inch.
The diameter grew in a day = 32%
The formula for the scale factor of dilation is = dimensions of a new shape/dimensions of a old shape
= 32%/1/2 = 0.32/0.5 = 0.64
b) Find the diameter of the mold after a day.
Answer:
The circular mold in a Petri dish has a diameter of 1/2
The diameter grew in a day = 32%
= 2 × 0.32 = 0.64
Therefore the diameter of the mold after a day = 0.64.
Question 19.
A figurine of the Statue of Liberty is 10 inches tall. The height of the Statue of Liberty is 150 feet. What is the scale factor of the dilation if the figurine is the image of the statue?
Answer:
Given that,
Figurine of the statue of Liberty is 10 inches tall
The height of the statue of Liberty is 150 feet.
The scalar factor of the dilation if the figurine is the image of the statue = figurine of the statue of Liberty/height of the statue of Liberty
Here 1 feet = 12 inches
150 inches = 150 × 12 = 1800
= 10/1800
= 1/180
= 0.005
Therefore, the scale factor of the dilation is 0.005 inches.
Question 20.
A spotlight is placed 2 feet from a 1-foot tall vase. A shadow 5 feet tall is cast on a wall as shown in the diagram. Find the distance of the vase from the wall.

Answer:
Given that,
The spotlight is placed 2 feets away from a 1 foot tall vase.
A shadow 5 feet tall is cast on a Wall.
Consider the distance from the vase to the wall is d.
The distance of a vase from the wall = distance of shadow from the spot light/distance of vase from the spotlight
= 2+d/2 = 5
= 2+d = 10
d = 10 – 2
d = 8
Therefore the distance from the vase to the wall is 8 feet.