Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 8 Lesson 8.5 Comparing Transformations to score better marks in the exam.
Math in Focus Grade 7 Course 3 B Chapter 8 Lesson 8.5 Answer Key Comparing Transformations
Math in Focus Grade 8 Chapter 8 Lesson 8.5 Guided Practice Answer Key
Technology Activity
Materials:
- geometry software
Compare Transformations With Geometry Software
Step 1.
Draw two line segments intersecting at a common endpoint using a geometry software program. Call the angle formed ∠AOB.
Step 2.
Measure their lengths and the angles they make with the x-axis. Record your results in the “before” cells of the second column in the following table.
Step 3.
Translate the angle in both the horizontal and vertical directions. Complete the second column of the table.
Step 4.
Reflect the angle in either the x- or y-axis. Complete the third column of the table.
Step 5.
Rotate the angle about the origin. Complete the fourth column of the table.
Step 6.
Dilate the angle by any nonzero scale factor and with any center. Complete the last column of the table.
Step 7.
Note which transformations preserve angle measure. Why does this guarantee that perpendicular lines will be preserved? Why does this guarantee that parallel lines will be preserved?
Math Journal Compare translations, reflections, rotations, and dilations. Discuss which ones preserve lengths, angle measures, perpendicular lines, and parallel lines.
Solve on graph paper. Show your work.
Question 1.
∆ABC is mapped onto ∆PQR, ∆LMN, and ∆XYZ as shown on the coordinate plane. State which transformation was used to obtain each image. Justify your answers.
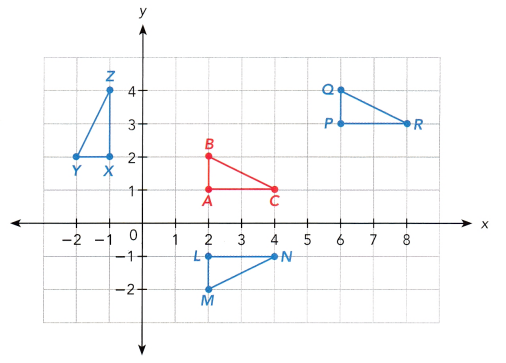
a) What transformation maps ∆ABC onto ∆PQR?
Answer:
The transformation maps ∆ABC onto the ∆PQR is translation.
Translation is a type of transformation that moves the figure on the coordinate plane without changing its orientation.
Here ∆ABC moves 2 units right through the x axis and it moves up 1 unit through the y axis.
b) What transformation maps ∆ABC onto ∆LMN?
Answer:
The transformation maps ∆ABC onto the ∆LMN is reflection.
Reflection means it is a type of transformation in which the image cutting out a preimage, lifting it, and putting it back face down is called reflection.
c) What transformation maps ∆ABC onto ∆XYZ?
Answer:
The transformation maps ∆ABC onto the ∆LMN is rotation.
Rotation means it is a type of transformation. It turns the image clockwise or counterclockwise but doesn’t change the image.
Here the image is rotated counterclockwise.
d) Compare the three transformations in terms of preserving lengths and angle measures.
Answer:
The three transformations are the transformation maps ∆ABC onto the ∆PQR is translation. After Changing ∆ABC onto the ∆PQR the length and angle measures are not changed.
The transformation maps ∆ABC onto the ∆LMN is reflection. After changing ∆ABC onto the ∆LMN the length and angle measures are not changed.
The transformation maps ∆ABC onto the ∆LMN is rotation. After Changing ∆ABC onto the ∆LMN the length is not changed but the angle measures are changed
You can use two vertices and their images to identify a transformation of one triangle onto another. But you should also use the third vertex and its image to check that other points of the figure are related by this transformation.

Math in Focus Course 3B Practice 8.5 Answer Key
Copy and complete on graph paper.
Question 1.
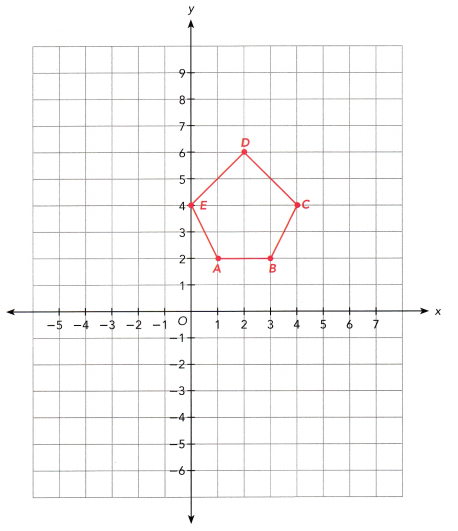
A curtain is made from a printed fabric with many pentagonal figures on it. One of the pentagons has coordinates A (1, 2), B (3, 2), C (4, 4), D (2, 6), and E (0, 4). Four other pentagons are images of ABCDE after each of the transformations in a) to d).
a) ABCDE is mapped onto FGHIJ by a translation of 8 units down. Draw FGHIJ.
Answer:
Given coordinates of Pentagon is
A (1, 2), B (3, 2), C (4, 4), D (2, 6), E (0, 4).
After translating the 8 units down the coordinates are F(1,-6), G(3,-6), H(4,-4), I(2,-2), J(0,-4).
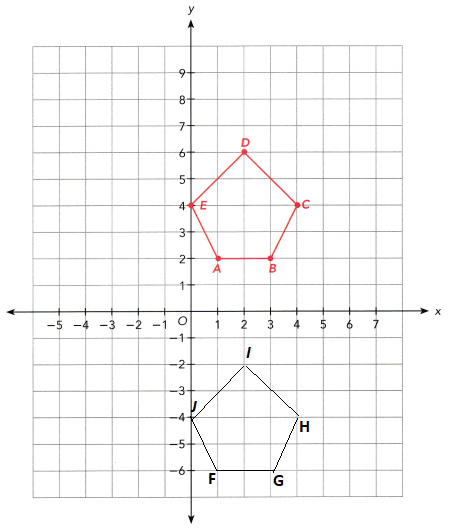
b) ABCDE is mapped onto KLMNP by a reflection about the y-axis. Draw KLMNP.
Answer:
Given coordinates of Pentagon is
A (1, 2), B (3, 2), C (4, 4), D (2, 6), E (0, 4).
After reflection to the y axis the coordinates are K(1,-2), L(3,-3), M(4,-4), N(2,-6) P(0,-4)
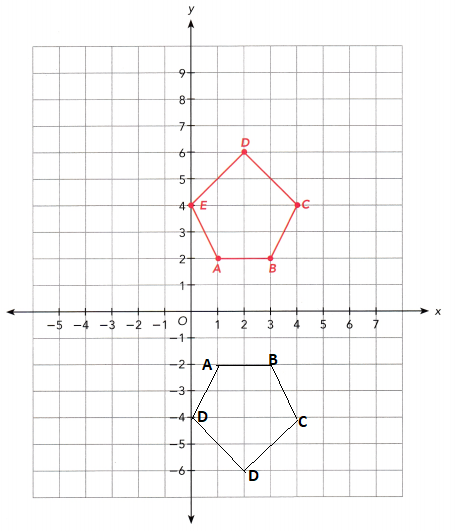
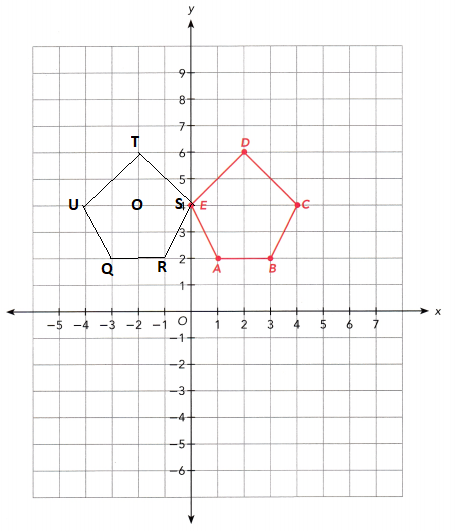
c) ABCDE is mapped onto QRSTU by a rotation 90° clockwise about the origin, O. Draw QRSTU.
Answer:
Given coordinates of Pentagon is
A (1, 2), B (3, 2), C (4, 4), D (2, 6), E (0, 4).
After rotation of 90⁰ clockwise the coordinates are Q(-3,2), R(-1,2), S(0,-4), T(-2,6), U(-4,4).
And point the origin as O.
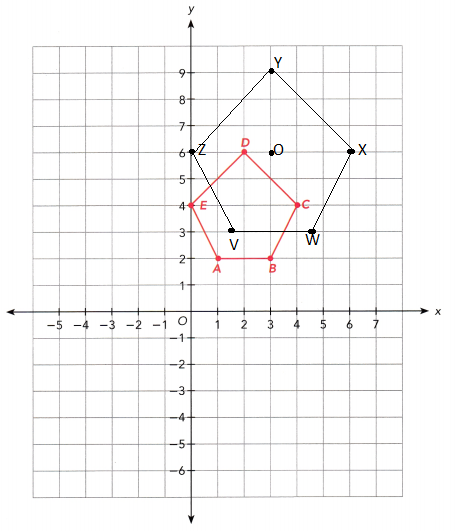
d) ABCDE is mapped onto VWXYZ by dilation with center at the origin and scale factor 1.5. Draw VWXYZ.
Answer:
Given that scale factor = 1.5
ABCDE is mapped onto VWXYZ by using the scale factor is 1.5 which means multiplying the coordinates with 1.5. then we get
A (1, 2) = V(1 × 1.5, 2 × 1.5) = (1.5,3)
B (3, 2) = W(3 × 1.5, 2 × 1.5) = (4.5,3)
C (4, 4) = X(4 × 1.5, 4 × 1.5) = (6,6)
D (2, 6) = Y(2 × 1.5, 6 × 1.5) = (3,9)
E (0, 4) = Z(0 × 1.5, 4 × 1.5) = (0,6)
e) Compare the four transformations in terms of lengths and angle measures of the pentagons.
Answer:
ABCDE is mapped onto FGHIJ by a translation of 8 units down. The length and angle measures of the pentagons are equal.
ABCDE is mapped onto KLMNP by a reflection about the y-axis. The length is the same but the angle measured is different from a pentagon.
ABCDE is mapped onto QRSTU by a rotation 90° clockwise about the origin. The length is the same but the angle is different from a pentagon.
ABCDE is mapped onto VWXYZ by a dilation with center at the origin and scale factor 1.5. The length and angle measures of a pentagon is different.
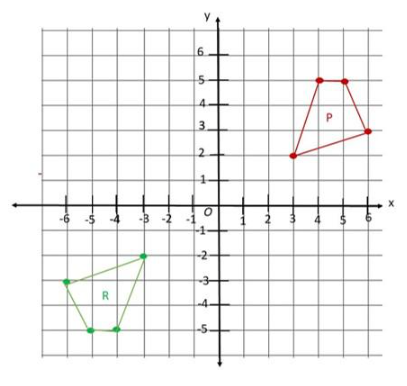
Question 2.
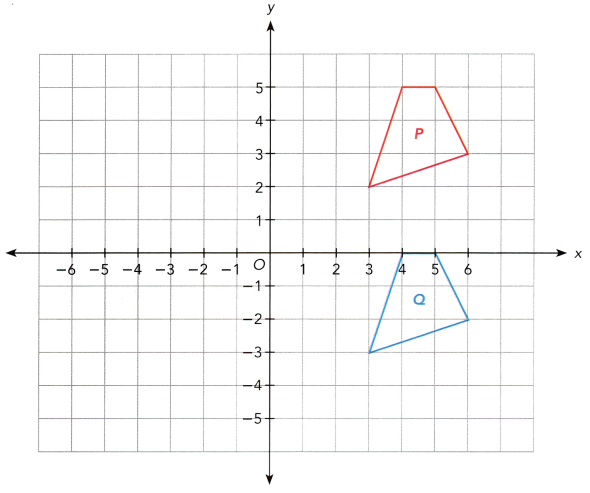
Quadrilateral P with coordinates (3, 2), (4, 5), (5, 5), and (6, 3) is mapped onto quadrilateral Q and R shown on the coordinate plane.
a) Describe the transformation from P to Q.
Answer:
The transformation from P to Q is translation. It means the figure on the coordinate plane moves without changing its orientation.
b) Quadrilateral P is mapped onto R by a half turn about the origin, O. Draw quadrilateral R.
Answer:
Note that a 180° rotation changes ttie coordinates from its original form (x, y) into (-x, -y). So, Figure P with points (3, 2), (4, 5), (5, 5) and (6, 3) will be mapped onto (-3,-2), (-4, -5), (-5, -5) and (-6, -3). Plotting these points then connecting it all determines image R.
c) The transformation that maps quadrilateral P onto quadrilateral R can be described in another way. Describe the transformation.
Answer:
The transformation that maps quadrilateral P onto quadrilateral R can be described in another way is reflection.
P with coordinates (3, 2), (4, 5), (5, 5), and (6, 3) after reflection the R coordinates are (3,-3), (6,-3), (5,-5), (4,-5).
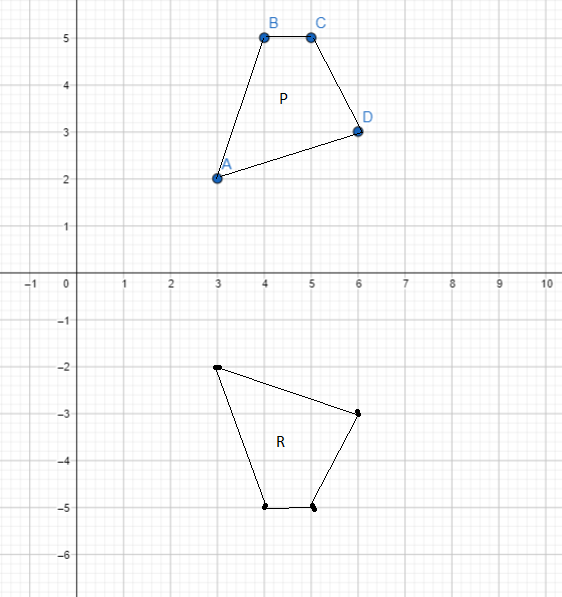
d) Compare the transformations in a) to c) in terms of the preservation of the shape and size of quadrilateral P.
Answer :
Question 3.
There are three arrow signs J, K, and L on a street. Jennifer is standing at the origin, O.
a) Arrow J tells Jennifer where the Kodak Theatre is. Arrow K is the reflection of arrow J in the line y = 3. Label arrow J.
Answer:
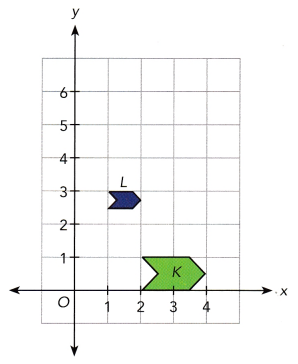
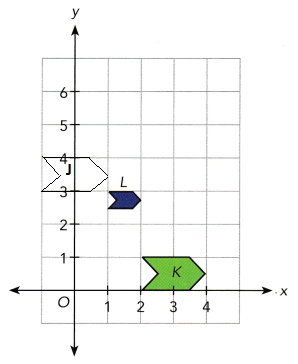
Here arrow K is on the X-axis and the K is the reflection of arrow J in the y axis.
b) Jennifer sees arrow L that is an image of arrow J. Describe the transformation that maps arrow J onto arrow L.
Answer:
The arrow L is the image of J. The transformation that maps arrow J onto L is dilation.
c) Compare the two transformations in terms of the shape and size of the arrows.
Answer:
Here we are comparing the two transformations the image K and image L is the reflection, the shape and size are the same. The image L and image J are dilation the shape and size are different.
Solve on graph paper. Show your work.
Question 4.
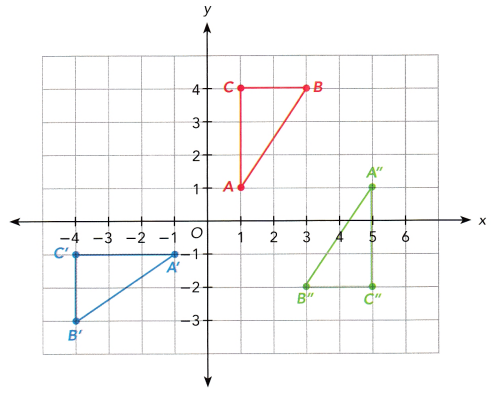
Triangle ABC is mapped onto triangle A’B’C’ and triangle A”B”C” as shown on the coordinate plane.
a) Triangle ABC is mapped onto triangle A’B’C’ by a reflection in the line l. On a copy of the graph, draw line l and label its equation.
Answer:
Here draw the line along the x axis with the equation of I = 1.
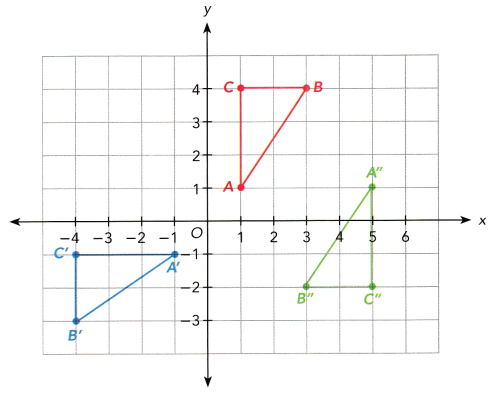
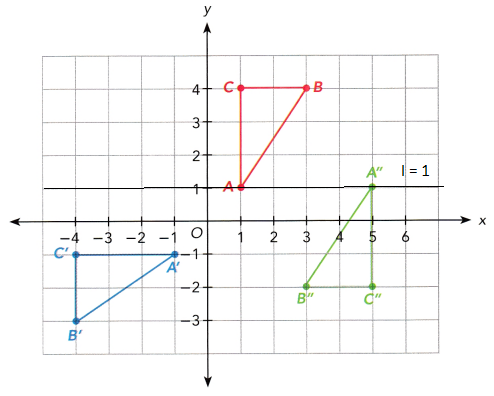
b) Triangle ABC is mapped onto triangle A”B”C” by a dilation with scale factor -1. Mark and label T as the center of dilation on the coordinate plane in a).
Answer:
Scale factor -1 is multiplied by the Triangle A”B”C”. Then it forms the transformation is dilation. Dilation means the image is enlarged or reduced. And mark the center of dilation is T.
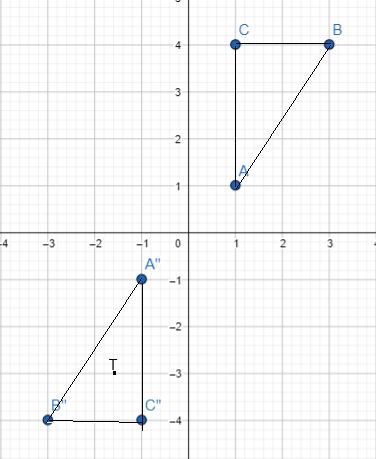
c) Describe another transformation that maps triangle ABC onto triangle A”B”C”.
Answer:
Here another transformation is the reflection. The triangle ABC is reflected as A”B”C”.
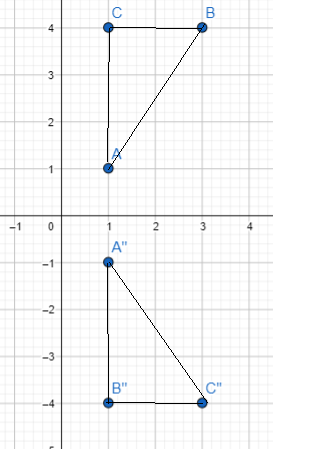
d) Compare the transformations that mapped triangle ABC onto triangle A’B’C’ and A”B”C” in terms of preservation of the shape and size of triangle ABC.
Answer:
The transformation of triangle ABC onto triangle A’B’C’ is the reflection and ABC onto triangle A”B”C” is the reflection and the dilation.
The transformation maps ∆ABC onto the ∆LMN is rotation.
Question 5.
∆ABC is mapped onto ∆A’B’C’ and ∆A”B”C”. The table of coordinates for the triangles is shown.

a) Draw ∆ABC, ∆A’B’C’, and ∆A”B”C”. Use 1 grid square on both axes to represent 1 unit for the interval from -5 to 7.
Answer:
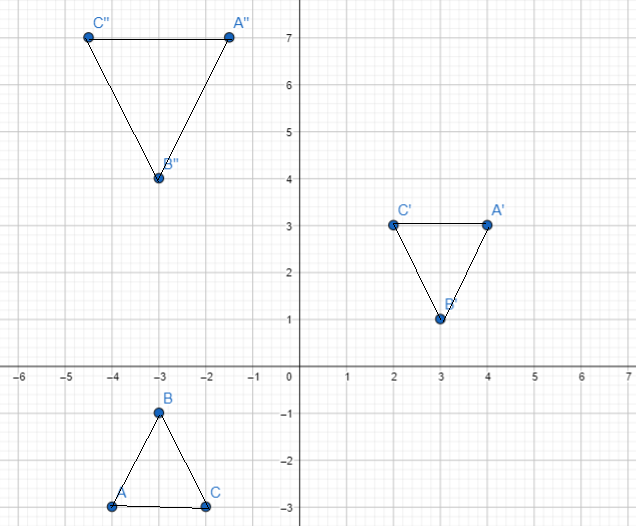
b) ∆ABC is mapped onto ∆A’B’C’ by a dilation with center at the origin, O, and scale factor-1. Describe another transformation that maps ∆ABC onto ∆A’B’C’.
Answer:
Observe that the points for triangle ABC are on (-4, -3), (-3, -1), and (-2, -3) whiLe the points for triangle A’B’C’ are on (4, 3), (3, 1), and (2, 3). Also, note that a 180: rotation changes the coordinates from its original form (x, y) into (-x, -y), which is the case for mapping triangle A’B’C’ from the original triangle. Therefore, the transformation is a 180° rotation.
c) What is the transformation that maps ∆ABC onto ∆A”B”C”?
Answer:
The transformation that maps triangle ABC onto Triangle A”B”C” is the dilation it means the figure is enlarged or reduced.
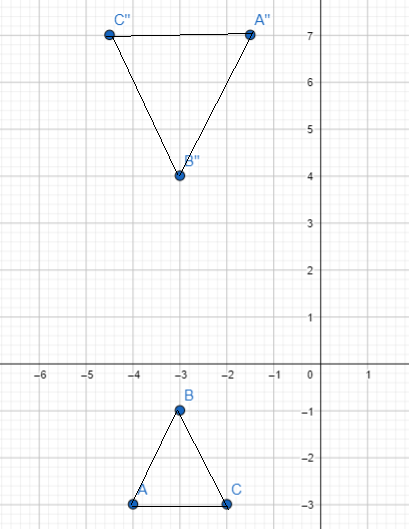
The transformation that maps ∆ABC onto ∆A”B” C” is the dilation which means the figure is enlarged or reduced.
d) Compare the transformations that mapped ∆ABC onto ∆A’B’C’ and ∆A”B”C” in terms of preservation of the shape and size of ∆ABC.
Answer:
Notice that the reflection and rotation only moves the original triangle ABC into different Location and also changes its angular position. The original triangle if compared to the image (∆A’B’C’) that undergo these transformation still has the same measure of sides and angles even after the transformations. However, triangle ABC and A”B”C” are different in sizes. Notice that the dilation for this case makes the image bigger.
Question 6.
Math Journal How do you describe a transformation that maps an equilateral triangle onto itself using each of the following: translation, reflection, rotation, and dilation?
Answer:
The target of this task is to give the description of the rotation, dilation, translation and reflection of an equilateral triangle that maps itself to itself.
For rotation, note that a full rotation is 360°. Of course, every figure rotated at this degree maps itself to itself. Another angle of rotation for an equilateral triangle is a 120° rotation. Since all the sides and angles of the equilateral triangle are congruent then mapping one vertex of the triangle to another will just produce the same triangle in terms of size, position, and shape. Everything will be just congruent Therefore, a rotation at 120° makes the equilateral triangle and its image the same.
For dilation, note that the only scale factor that does not change orientation and size of any figure is 1. Therefore, the dilation at a scale of 1 makes the equilateral triangle and its image the same.
For the reflection, observe the altitude of the equilateral triangle. Creating a line of symmetry in this part of the triangle, divides the triangle into two equal parts. Thus, all the points have the same distance with its symmetric half from this Line. Therefore, the reflection of that makes the equiLateral triangle and its image the same is at the altitude of the triangle.
For the translation, there is no translation for an equilateral triangle that makes the triangle and its image the same. Since, if one vertex of the equilateral triangle moves up or down, or left or right all of its vertex will move that way, thus the whole triangle will move and change its location, unless the translation is 0.
Brain @ Work
Question 1.
A two-blade table fan is coded with two digits for easy identification. Each blade in the horizontal position shown in the picture is painted with the two-digit number. What number should be used so that when the blades make a half turn, the number will be read correctly?

Answer:
The goal is to determine the two-digit numbers that should e printed in the two-blade fan so that when it has rotated at an angle of 180° the number will not be upside down The trick is to choose two two-digit numbers for each blade that wherever the position of the blade is, horizontally, the number will stilt look the same. Consider numbers 11 and 69, at the original horizontal state of the blade, blade 11 will be at the right while blade 69 will be at the left After the rotation, blade 69 will be at the right while blade 11 will be at the left both can still be read correctly.
Question 2.
Line P with equation y = x + 2 maps onto line Q with equation y = -x + 4.
a) Describe a reflection that maps line P onto line Q.
Answer:
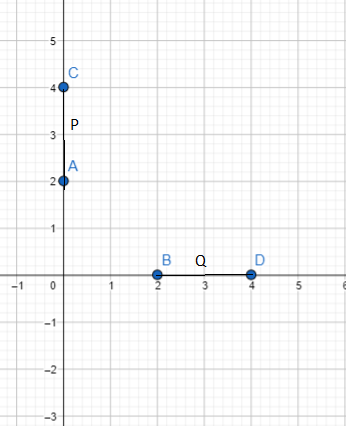
b) Describe a rotation that maps line P onto line Q.
Answer: Rotation means changing the figure clockwise or counterclockwise in the given equation line P rotation in the clockwise direction.
Question 3.
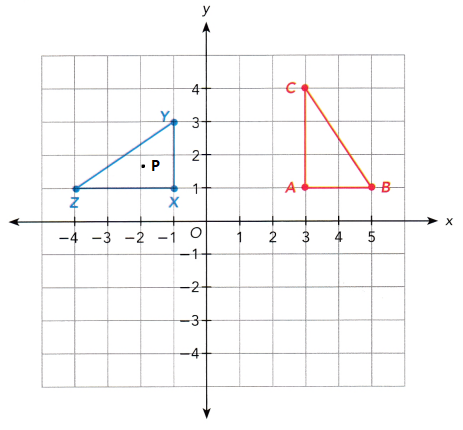
Triangle ABC is mapped onto triangle XYZ by a rotation 270° clockwise about center P. Both triangles are shown on the coordinate plane below. On a copy of the graph, mark and label the center P. What are the coordinates of center P? Explain how you found your answer.
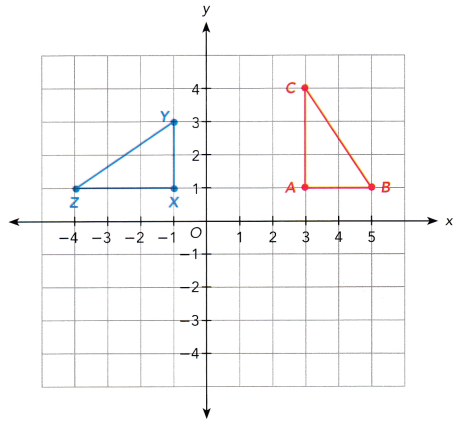
Answer:
Plot the point P on the rotation 270° clockwise figure. The coordinates of the P are x(-1,1), y(-1,3) and z(-4,3).
Question 4.
After a rain, a circular puddle shrunk steadily for two days in the sun. The puddle was 8 inches in diameter initially. It shrunk by a scale factor each day. After two days, the diameter of the puddle was 6.48 inches. What is the scale factor of dilation? Explain how you found your answer.
Answer:
Given that the circular puddle shrunk steadily for two days in the sun then the diameter of a puddle is 8 inches.
After two days the diameter of a puddle is 6.48 inches.
Scale factor = Diameter of a changed puddle/ Diameter of an original puddle
= 6.48 inches/8 inches
= 0.81 inches
Therefore the scalar factor of a dilation is 0.81 inches.