This handy Math in Focus Grade 8 Workbook Answer Key Chapter 9 Congruence and Similarity detailed solutions for the textbook questions.
Math in Focus Grade 8 Course 3 B Chapter 9 Answer Key Congruence and Similarity
Math in Focus Grade 8 Chapter 9 Quick Check Answer Key
Complete.
Question 1.
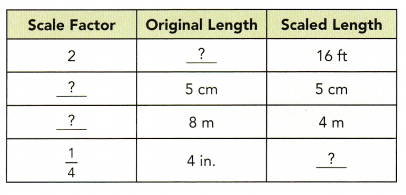
Answer:
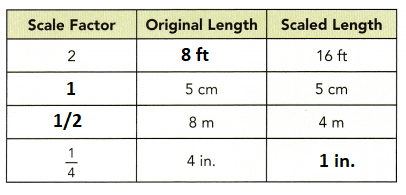
Explanation:
1. Scale factor: 2
2 × 8ft = 16 ft
2. Original length = 5
Scaled length = 5
Scale factor = 5/5 = 1
3. Original length = 8 m
Scaled length = 4 m
Scale factor = scale/actual = 4/8 = 1/2
4. Scale factor = 1/4
Original length = 4 inches
We know that
scale factor = scale/actual
1/4 = scale length/4
scaled length = 4/4
scaled length = 1 in.
Solve.
Question 2.
Shawn built a model of a ship whose length was 4,500 inches. His model was 15 inches long. Find the scale factor.
Answer:
Let the scale factor be x
Shawn built a model of a ship whose length was 4,500 inches.
His model was 15 inches long.
x × 15 = 4500
x = 4500/15
x = 300 inches
Question 3.
A line segment is 4 centimeters long. When projected on a screen, the line segment is 20 centimeters long. Find the scale factor.
Answer:
Let the scale factor be x
scale factor = scale/actual
Actual length = 4 cm
scaled length = 20 cm
scale factor = 20 cm/4 cm
scale factor = 5 cm
Thus the scale factor is 5 cm.
Question 4.
A model plane is built with a scale factor of \(\frac{1}{180}\). The actual length of the plane is 210 feet (2,520 inches). Find the length of the model.
Answer:
Given,
A model plane is built with a scale factor of \(\frac{1}{180}\).
The actual length of the plane is 210 feet (2,520 inches).
Scale/Actual = 1/180
1/180 = l/210 feet
210/180 = length
Length = 210/180
Length = 21/18
Length = 7/6
Length = 1.16 feet
Question 5.
The scale of a map is 2 inches : 3 kilometers. The length of a road on the map is 3 inches. Find the actual length of the road.
Answer:
Given,
The scale of a map is 2 inches : 3 kilometers.
The length of a road on the map is 3 inches
Let the actual length of the road be x.
2 in./ 3 km = 3 in / x km
x = (3 × 3)/2
x = 9/2 = 4.5 km
Thus the actual length of the road is 4.5 kilometers.
Question 6.
The diagram shows a plot of land ABCD drawn on a map.
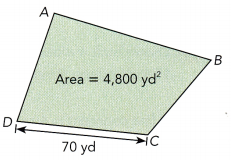
a) On the map, \(\overline{C D}\) is 1\(\frac{3}{4}\) inches. Find the scale of the map.
Answer:
b) Find the area of ABCD on the map.
Answer:
The measures of two interior angles are given for each triangle. Find the measure of the third interior angle.
Question 7.
△ABC: 20°, 80°
Answer:
Given
△ABC: 20°, 80°
The sum of interior angles of the triangle = 180°
∠a + ∠b + ∠c = 180°
20°+ 80° + ∠c = 180°
100° + ∠c = 180°
∠c = 180° – 100°
∠c = 80°
Thus the measure of the third interior angle is 80°
Question 8.
△KLM: 37°, 76°
Answer:
Given,
△KLM: 37°, 76°
The sum of interior angles of the triangle = 180°
∠k + ∠l + ∠m = 180°
37°+ 76° + ∠m = 180°
113° + ∠m = 180°
∠m = 180° – 113°
∠m = 67°
Thus the measure of the third interior angle is 67°
Question 9.
△PQR: 15°, 103°
Answer:
Given,
△PQR: 15°, 103°
The sum of interior angles of the triangle = 180°
∠p + ∠q + ∠r = 180°
15°+ 103° + ∠r = 180°
∠r = 180° – 118°
∠r = 62°
Find the unknown angle measure.
Question 10.
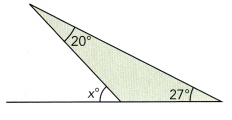
Answer:
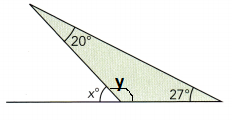
Let the unknown angle be y
The sum of three angles = 180°
20° + 27° + y = 180°
47° + y = 180°
y = 180° – 47°
y = 133°
x° + y° + 27° = 180°
x° + 133° + 27° = 180°
x° = 180° – 133° – 27°
x° = 20°
Thus the unknown angle is 20°
Question 11.
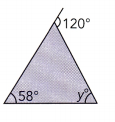
Answer:
y° + y° = 120°
2y° = 120°
y = 120°/2
y =60°
Solve for each variable.
Question 12.
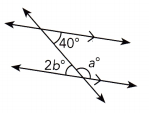
Answer:
a° + 2b° = 180
b° = 40° (alternate angles)
2b° = 80°
a° + 2b° = 180
a° + 80° = 180°
a° = 180° – 80°
a° = 100°
Question 13.
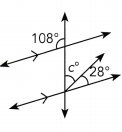
Answer:
c° + 28° = 180°
c° = 180° – 28°
c° = 152°