Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 5 Review Test to score better marks in the exam.
Math in Focus Grade 8 Course 3 A Chapter 5 Review Test Answer Key
Concepts and Skills
Solve each system of linear equations using the elimination method.
Question 1.
3x + 2y = 18
2x + 3y = 22
Answer:
3x + 2y = 18 Equation 1
2x + 3y = 22 Equation 2
We are given the system of equations:
2 ∙ (3x + 2y) = 2 ∙ 18 We can eliminate first either x, or y.
6x + 4y = 36 Equation 3 We usually choose to eliminate the variable which has smaller coefficients, in this case both have the same coefficients. We choose to eliminate x.
Multiply Equation 1 by 2:
3 ∙ (2x + 3y) = 3 ∙ 22 Multiply Equation 2 by 3:
6x + 9y = 66 Equation 4
(6a + 9y — (6x + 4y) = 66 — 36 We subtract Equation 3 from Equation 4:
6x + 9y — 6x — 4y = 30 Use the distributive property:
5y = 30 Simplify, 6x is eliminated:
\(\frac{5 y}{5}\) = \(\frac{30}{5}\) Divide by 5 and simplify:
y = 6
3x + 2(6) = 18 Substitute 6 for y in Equation 1:
3x + 12 = 18 Simplify:
Subtract 12 from both sides:
3x + 12 — 12 = 18 — 12
3x = 6 Simplify:
\(\frac{3 x}{3}\) = \(\frac{6}{3}\) Divide by 3:
x = 2
y = 6 The solution to the system of linear equations is
x = 2
y = 6
Question 2.
5x + y = 8
x + 3y = 10
Answer:
5x + y = 8 Equation 1 We are given the system of equations:
x + 3y = 10 Equation 2
3 ∙ (5x + y) = 3 ∙ 8 We can eliminate first either x, or y.
15x + 3y = 24 Equation 3 We usually choose to eliminate the variable which has smaller coefficients, in this case y. Multiply Equation 1 by 3:
(15x + 3y) – (x + 3y) = 24 – 10 We subtract Equation 2 from Equation 3:
15x + 3y – x – 3y = 14 Use the distributive property:
14x = 14 Simplify, 3y is eliminated:
\(\frac{14 x}{14}\) = \(\frac{14}{14}\)
Divide by 14 and simplify:
x = 1
5(1) + y = 8 Substitute 1 for x in Equation 1:
5 + y = 8 Simplify:
5 + y – 5 = 8 – 5 Subtract 5 from both sides:
y = 3 Simplify:
x = 1
The solution to the system of linear equations is
y = 3
x = 1; y = 3
Question 3.
\(\frac{1}{2}\)a + b = 7
a + 3b = 19
Answer:
\(\frac{1}{2}\)a + b = 7 Equation 1
a + 3b = 19 Equation 2
We are given the system of equations:
2 ∙ (\(\frac{1}{2}\)a + b) = 7 We can eliminate rirst either a, or b
a + 2b = 14 Equation 3 We usually choose to etiminate the variable which has smaller coefficients, in this case a.
Multiply Equation 1 by 2:
(a + 3b) — (a + 2b) = 19 — 14 We subtract Equation 3 from Equation 2:
a + 3b — a — 2b = 5 Use the distributive property
b = 5 Simplify, a is eliminated:
a + 3(5) = 19 Substitute 5 for b in Equation 2:
a + 15 = 19 Simplify:
a + 15 — 15 = 19 — 15 Subtract 15 from both sides:
a = 4 Simplify:
a = 4 The solution to the system of linear equations is
b = 5
a = 4 ; b = 5
Solve each system of linear equations using the substitution method.
Question 4.
a + 2b = 1
2a + b = 8
Answer:
a + 2b = 1 Equation 1 We are given the system of equations:
2a + b = 8 Equation 2
2a + b = 8 Use Equation 2 to express b in terms of a:
2a + b — 2a = 8 — 2a Subtract 2a from both sides:
b = 8 — 2a Equation 3 Simplify:
a + 2(8 — 2a) = 1 Substitute Equation 3 into Equation 1:
a + 16 — 4a = 1 Use the distributive property:
—3a + 16 = 1 Simplify:
—3a + 16 — 16 = 1 — 16 Subtract 16 from both sides:
—3a = —15 Simplify:
\(\frac{-3 a}{-3}\) = \(\frac{-15}{-3}\) Divide by -3:
a = 5 Simplify:
b = 8 — 2(5) Substitute 5 for a in Equation 3:
= 8 — 10
= -2
a = 5 The solution of the system ¡S:
b = -2
a = 5; b = -2
Question 5.
2x + 11y = 15
x – y = 1
Answer:
2x + 11y = 15 Equation 1 We are given the system of equations:
x — y = 1 Equation 2
x — y = 1 Use Equation 2 to express x in terms of y:
x – y + y = 1 + y Add y to both sides:
x = y + 1 Equation 3 Simplify:
2(y + 1) + 11y = 15 Substitute Equation 3 into Equation 1:
2y + 2 + 11y = 15 Use the distributive property:
13y + 2 = 15 Simplify:
13y + 2 — 2 = 15 — 2 Subtract 2 from both sides:
13y = 13 Simplify:
\(\frac{13 y}{13}\) = \(\frac{13}{13}\) Divide by 13:
y = 1 Simplify:
x = 1 + 1
= 2 Substitute 1 for y in Equation 3:
x = 2 The solution of the system is:
y = 1
x = 2
y = 1
Question 6.
\(\frac{1}{2}\)x + \(\frac{1}{2}\)y = 7
3x – y = 22
Answer:
We are given the system of equations:
\(\frac{1}{2}\)x + \(\frac{1}{2}\)y = 7 Equation 1
3x — y = 22 Equation 2
3x — y = 22 use Equation 2 to express y is terms of x:
3x — y — 3x = 22 — 3x Subtract 3x from both sides:
—y = 22 — 3x Simplify:
y = 3x — 22 Equation 3
\(\frac{1}{2}\)x + \(\frac{1}{2}\)(3x – 22) Substitute Equation 3 into Equation 1:
2 • \(\frac{1}{2}\)x + 2 • \(\frac{1}{2}\)(3x —22) = 2 • 7 Multiply both sides by 2:
x + 3x — 22 = 14 Simplify:
4x — 22 = 14
4x — 22 + 22 = 14 + 22 Add 22 to both sides:
4x = 36 Simplify:
\(\frac{4 x}{4}\) = \(\frac{36}{4}\) Divide by 4
x = 9 Simplify:
y = 3(9) — 22 Substitute 9 for x in Equation 3:
= 27 — 22
= 5
x = 9 The solution of the system is:
y = 5
x = 9
y = 5
Solve each system of linear equations using the graphical method. Use 1 grid square to represent 1 unit on both axes for the interval -3 to 8.
Question 7.
2x + 3y = 24
2x + y = 12
Answer:
2x + 3y = 24 Equation 1
2x + y = 12 Equation 2
We are given the system of equations:
2x + 3y = 24 We rewrite Equation 1 in slope-intercept form:
2x + 3y – 2x = 24 — 2x
3y = —2x + 24
\(\frac{3 y}{3}\) = \(\frac{-2 x+24}{3}\)
y = –\(\frac{2}{3}\)x + 8
2x + y = 12 we rewrite Equation 2 in slope-intercept rorm:
2x + y – 2x = 12 — 2x
y = —2x + 12
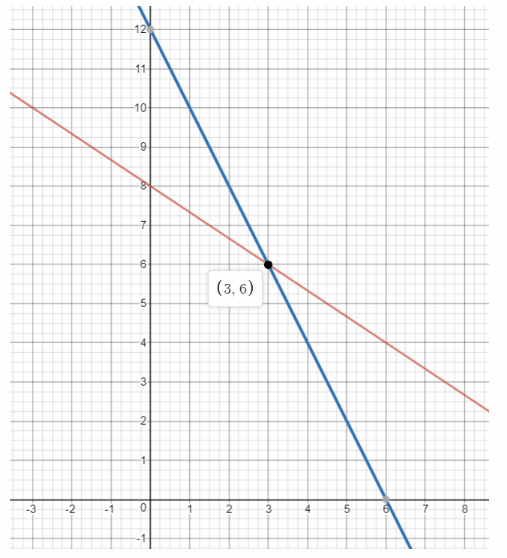
We graph the two equations: the first has slope —\(\frac{2}{3}\) and y-intercept 8, while the second has slope -2 and y-intercept 12:
x = 3 The point of intersection is (3, 6). Therefore the solution of the system of equations is
y = 6
x = 3; y = 6
Question 8.
2x + 5y = 1
3x – y = – 7
Answer:
2x + 5y = 1 Equation 1
3x – y = —7 Equatiou 2
We are given the system of equations:
2x + 5y = 1 We rewrite Equation 1 in slope-intercept form:
2x + 5y — 2x = 1 — 2x
5y= —2x + 1
\(\frac{5 y}{5}\) = \(\frac{-2 x+1}{5}\)
y = –\(\frac{2}{5}\)x + \(\frac{1}{5}\)
3x — y = —7 We rewrite Equation 2 in slope-intercept form:
3x — y — 3x = —7 — 3x
—y = —3x — 7
y = 3x + 7
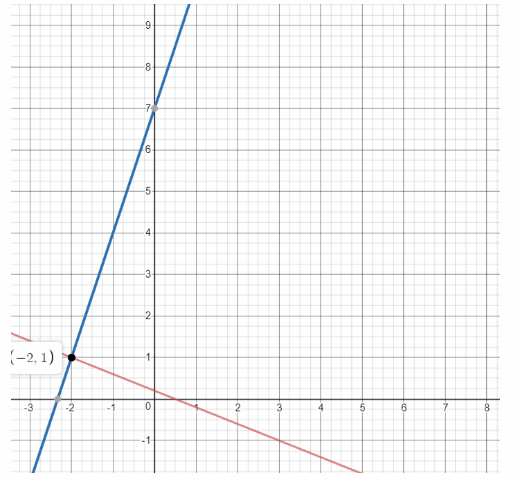
We graph the two equations: the first has slope —\(\frac{2}{5}\) and y-intercept \(\frac{1}{5}\), while the second has slope 3 and y-intercept 7:
x = -2 The point of intersection is (—2, 1). Therefore the solution of the system of equations is:
y = 1
x = —2; y = 1
Question 9.
x + 0.5y = 6
3x – y = 13
Answer:
x + 0.5y = 6 Equation 1
3x — y = 13 Equation 2
We are given the system of equations:
x + 0.5y = 6 We rewrite Equation 1 in stope-intercept form:
x + 0.5y — x = 6 — x
0.5y = —x + 6
\(\frac{0.5 y}{0.5}\) = \(\frac{-x+6}{0.5}\)
y = -2x + 12
3x — y = 13 We rewrite Equation 2 in slope-intercept form:
3x — y — 3x = 13 — 3x
—y = —3x + 13
y = 3x — 13
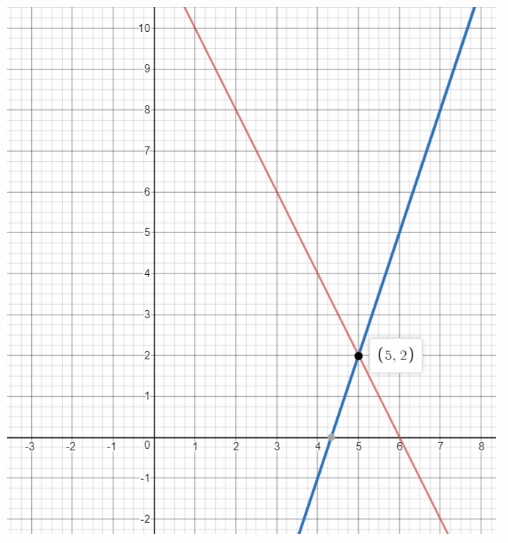
We graph the two equations: the first has slope -2 and y-intercept 12. while the second has slope 3 and y-intercept -13:
x = 5 The point of intersection is (5, 2). Therefore the solution of the system of equations is
y = 2
x = 5; y = 2
Solve each system of linear equations. Explain your choice of method.
Question 10.
x = 4y – 1
2x – 6y = – 1
Answer:
x = 4y — 1 Equation 1 We are given the system of equations:
2x — 6y = —1 Equation 2
5x + y = 15 As there is a variable with coefficient 1 (which is x in Equation 1), we can use the substitution method.
x = 4y — 1 Equation 1 expresses x is terms of y:
2(4y – 1) – 6y = —1 Substitute Equation 1 into Equation 2:
8y — 2 – 6y = —1 Use the distributive property
2y — 2 = —1 Simplify:
2y — 2 + 2 = —1 + 2 Add 2 to both sides:
2y = 1 Simplify:
\(\frac{2 y}{2}\) = \(\frac{1}{2}\) Divide by 2:
y = \(\frac{1}{2}\) simplify
x = 4(\(\frac{1}{2}\)) – 1 Substitute \(\frac{1}{2}\) for y in Equation 1:
= 2 – 1
= 1
x = 1 The solution of the system is
y = \(\frac{1}{2}\)
x = 1
y = \(\frac{1}{2}\)
Question 11.
3x – 14y = -49
5x + 2y = 45
Answer:
3x — 14y = -49 Equation 1
5x + 2y = 45 Equation 2
We are given the system of equations:
7 • (5x + 2y) = 7 . 45 The substitution method would lead to fractions as none of the variables has coefficient 1.
35x + 14y = 315 Equation 3
We use the elimination method.
We can eliminate first either z, or g.
We choose to eliminate the variable y because -14 is multiple of 2.
Multiply Equation 2 by 7:
(3x — 14y) + (35x + 14y) = —49 + 315 We add Equation 3 to Equation 1:
3x — 14y + 35x + 14y = 266 Simplify, 14y is eliminated:
38x = 266
\(\frac{38 x}{38}\) = \(\frac{266}{38}\) Divide by 38 and simplify
x = 7
5(7) + 2y = 45 Substitute 7 for x in Equation 2:
35 + 2y = 45 Simplify:
35 + 2y — 35 = 45 — 35 Subtract 35 from both sides:
2y = 10 Simplify:
\(\frac{2 y}{2}\) = \(\frac{10}{2}\) Divide by 2
y = 5 simplify
x = 7 The solution to the system of linear equations is
y = 5
x = 7
y = 5
Question 12.
x – \(\frac{1}{3}\)y = 6
2x + y = 2
Answer:
x – \(\frac{1}{3}\)y = 6 Equation 1
2x + y = 2 Equation 2
We are given the system of equations:
x – \(\frac{1}{3}\)y = 6 We can use substitution or graphical method as we have at least one variable with coefficient 1. We choose the graphical method
x – \(\frac{1}{3}\)y – x = 6 – x
–\(\frac{1}{3}\)y = -x + 6 We rewrite Equation 1 in slope-intercept form:
—3(\(\frac{1}{3}\)y) = —3(—x + 6)
y = 3x— 18
2x + y = 2 We rewrite Equation 2 in slope-intercept form:
2x + y — 2x = 2— 2x
y = —2x + 2
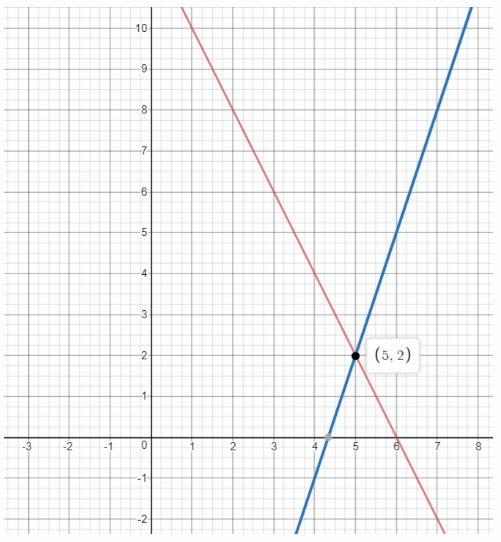
We graph the two equations: the first has slope 3 and y-intercept -18, while the second has slope -2 and y-intercept 2:
x = 5 The point of intersection is (5, 2). Therefore the solution of the system of equations is
y = 2
x = 5
y = 2
Identify whether each system of equations is inconsistent, dependent, or has a unique solution. Justify your answer. Solve the system of linear equations if it has a unique solution.
Question 13.
3x + 2y = 8
6x + 4y = 16
Answer:
3x + 2y = 8 Equation 1
6x + 4y = 16 Equation 2
we are given the system of equations
3x + 2y = 8 Rewrite Equation 1 in slope-intercept form y = mx + b
3x + 2y – 3x = 8 – 3x Subtract 3x from both sides and simplify
2y = -3x + 8
\(\frac{2 y}{2}\) = \(\frac{-3 x+8}{2}\) Divide both sides by 2 and simplify
y = \(-\frac{3}{2} x\) + 4
6x + 4y = 16 Rewrite Equation 2 in slope-intercept form y = mx + b:
6x + 4y — 6x = 16 — 6x Subtract 6x from both sides and simplify:
4y = —6x + 16
\(\frac{4 y}{4}\) = \(\frac{-6 x+16}{4}\) Divide both sides by 4 and simplify:
y = \(-\frac{3}{2} x\) + 4
Since Equation 1 and Equation 2 are equivalent, they have an infinite number of solutions.
Therefore system of linear equations is dependent
Dependent
Question 14.
\(\frac{x}{3}\) + y = 8
x + 3y = 10
Answer:
\(\frac{1}{3} x\) + y = 8 Equation 1
x + 3y = 10 Equation 2
We are given the system of equations:
\(\frac{1}{3} x\) + y = 8
Rewrite Equation 1 in slope-intercept form y = mx + b:
\(\frac{1}{3} x\) + y – \(\frac{1}{3} x\) = 8 – \(\frac{1}{3} x\) Subtract \(\frac{1}{3} x\) from both sides and simplify:
y = –\(\frac{1}{3} x\) + 8
x + 3y = 10 Rewrite Equation 2 in slope-intercept form y = mx + b
x + 3y — x = 10 — x Subtract x from both sides and simplify:
\(\frac{3 y}{3}\) = \(\frac{-x+10}{3}\) Divide both sides by 3 and simplify:
y = \(-\frac{1}{3} x\) + \(\frac{10}{3}\)
The linear equations have the same slope and different y-intercept. The system of linear equations is inconsistent because the system of Linear equations has no solution.
Inconsistent
Question 15.
\(\frac{1}{2}\)x + y = 7
x + 2y = 14
Answer:
\(\frac{1}{2}\)x + y = 7 Equation 1
x + 2y = 14 Equation 2
We are given the system of equations:
\(\frac{1}{2}\)x + y = 7 Rewrite Equation 1 in slope-intercept form y = mx + b:
\(\frac{1}{2}\)x + y — \(\frac{1}{2}\)x = 7 — \(\frac{1}{2}\)x Subtract \(\frac{1}{2}\)x from both sides and simplify:
y = –\(\frac{1}{2}\)x + 7
x + 2y = 14 Rewrite Equation 2 in slope-intercept form y = mx + b:
x + 2y — x = 14 — x Subtract x from both sides and simplify:
\(\frac{2 y}{2}\) = \(\frac{-x+14}{2}\) Divide both sides by 2 and simplify:
Since Equation 1 and Equation 2 are equivalent they have an infinite number of solutions.
Therefore system of linear equations is dependent.
Dependent
Question 16.
2x – \(\frac{1}{2}\)y = 10
y = 4x + 11
Answer:
2x — \(\frac{1}{2}\)y = 1o Equation 1
y = 4x + 11 Equation 2
We are given the system of equations:
2x – \(\frac{1}{2}\)y = 10 Rewrite Equation 1 in slope-intercept form y = mx + b:
2x – \(\frac{1}{2}\)y – 2x = 10 – 2x Subtract 2x from both sides and simplify:
–\(\frac{1}{2}\)y = -2x + 10
-2 ∙ (-\(\frac{1}{2}\)y) = -2(-2x + 10) Multiply both sides by -2 and simplify
y = 4x — 20
y = 4x + 11 Equation 2 is written in slope-intercept form y = mx + b
The linear equations have the same slope and different y-intercept The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent
Question 17.
2x – 5y = -21
4x + 3y = 23
Answer:
2x — 5y = —21 Equation 1
4x + 3y = 23 Equation 2
We are given the system of equations:
2(2x — 5y) = 2(—21) We use the elimination method.
4x — 10y = —42 Equation 3 Multiply Equation 1 by 2:
(4x + 3y) — (4x — 10y) = 23 — (—42) We subtract Equation 3 from Equation 2 and simplify:
4x + 3y — 4x + 10y = 65
13y = 65
\(\frac{13 y}{13}\) = \(\frac{65}{13}\) Divide by 13 and simplify:
y = 5
4x + 3(5) = 23 Substitute 5 for y in Equation 2:
4x + 15 = 23
4x + 15 — 15 = 23 — 15 Subtract 15 from both sides and simplify:
4x = 8
The system of linear equations has an unique solution:
\(\frac{4 x}{4}\) = \(\frac{8}{4}\) Divide by 4 and simplify:
x = 2
x = 2 The system of Linear equations has an unique solution:
y = 5
Unique solution (x = 2, y = 5)
Question 18.
6y – 12x = 60
4y – 40 = 8x
Answer:
6y — 12x = 60 Equation 1
4y — 40 = 8x Equation 2
We are given the system of equations:
6y — 12x = 60 Rewrite Equation 1 in slope-intercept form y = mx + b:
6y — 12x + 12x = 60 + 12x Add 12x to both sides and simplify
6y = 12x + 60
\(\frac{6 y}{6}\) = \(\frac{12 x+60}{6}\) Divide both sides by 6 and simplify:
y = 2x + 10
4y – 40 = 8x Rewrite Equation 2 in slope-intercept form y = mx + b
4y — 40 + 40 = 8x + 40 Add 40 to both sides and simplify:
4y = 8x + 40
\(\frac{4 y}{4}\) = \(\frac{8 x+40}{4}\) Divide both sides by 4 and simplify:
y = 2x + 10
Since Equation 1 and Equation 2 are equivalent, they have an infinite number of solutions. Therefore system of linear equations is dependent
Dependent
Problem Solving
Solve. Show your work.
Question 19.
Andy and Ben both worked a total of 88 hours one week. Ben worked 8 hours more than Andy. Find the number of hours each man had worked.
Answer:
Lets note:
a = the number of hours worked by Andy
b = the number of hours worked by Ben
a + b = 88 Equation 1 We write the system of equations:
b = a + 8 Equation 2
We use the substitution method.
b is expressed in terms of a in Equation 2:
a + (a + 8) = 88 Substitute Equation 2 into Equation 1:
a + a + 8 = 88 Simplify:
2a +8 = 88
2a + 8 – 8 = 88 — 8 Subtract 8 from both sides:
2a = 80 Simplify:
\(\frac{2 a}{2}\) = \(\frac{80}{2}\) Divide both sides by 2:
a = 40 simplify
b = 40 + 8 Substitute 40 for a in Equation 2:
= 48
So Andy worked 40 hours and Ben worked 48 hours
Andy: 40 hours
Ben: 48 hours
Question 20.
In three years’ time, Mr. Sullivan will be 3 times as old as his daughter. Six years ago, he was 6 times as old as she was. How old are they now?
Answer:
s + 3 = 3(d + 3) Equation 1
s — 6 = 6(d — 6) Equation 2
Lets note:
s = Mr Sullivans age now
d = the daughters age now
We can write the system of equations:
s — 6 = 6d — 36 We use the substitution method.
s — 6 + 6 = 6d — 36 + 6 Rewrite Equation 2 to express s in terms of d:
s = 6d — 30 Equation 3
(6d — 30) + 3 = 3(d + 3) Substitute Equation 3 in Equation 1 and simplify:
6d — 30 + 3 = 3d + 9
6d — 27 = 3d + 9
6d — 27 – 3d = 3d + 9 – 3d We subtract 3d from both sides:
3d — 27 = 9
3d — 27 + 27 = 9 + 27 Add 27 to both sides:
3d = 36
\(\frac{3 d}{3}\) = \(\frac{36}{3}\) Divide by 3 and simplify:
d = 12
s = 6(12) — 30 Substitute 12 for d in Equation 3:
= 72 – 30
= 42
d = 12 The solution to the system of linear equations is:
s = 42
Mr Sullivan’s age is 42 years, while his daughter’s is 12 years now
Mr Sullivan: 42 years
The daughter: 12 years
Question 21.
Samantha has a riddle for her sister: Find a pair of integers x and y that satisfy 7x + 3y = 64 and one of the integers is 3 times the other.
Answer:
7x + 3y = 64 Equation 1
x = 3y Equation 2
We write the systems of equations:
7x + 3y = 64 Equation 1
y = 3x Equation 2
x = 3y Equation 1 We solve the first system using substitution.
7(3y) + 3y = 64 Substitute Equation 2 into Equation 1:
21g + 3y = 64
24y = 64
\(\frac{24 y}{24}\) = \(\frac{64}{24}\) We determine y:
y = \(\frac{8}{3}\)
As y is not integer, this is not a solution.
y = 3x Equation 2 We solve the second system using substitution.
7x + 3(3x) = 64 Substitute Equation 2 into Equation 1:
7x + 9x = 64
16x = 64
\(\frac{16 x}{16}\) = \(\frac{64}{24}\) We determine x:
x = 4
y = 3(4) Substitute 4 for x in Equation 2:
= 12
x = 4 The two integers are 4 and 12.
y = 12
x = 4
y = 12
Question 22.
The shape ABC in the quilt block below is an isosceles triangle. In triangle ABC, AB = AC. The perimeter of triangle ABC is 27.3 inches. Find the values of x and y. Then find the length of each side of the triangle in inches.
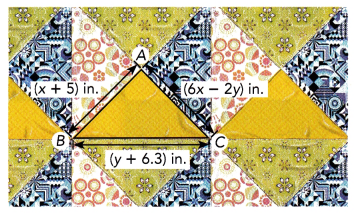
Answer:
x + 5 = 6x — 2y Equation 1
2(x + 5) + y + 6.3 = 27.3 Equation 2 We can write the system of equations:
x + 5 – x = 6x — 2y — x Equation 1
2x + 10 + y + 6.3 = 27.3 Equation 2
we bring me system to the standard form:
5x — 2y = 5 Equation 1
2x + y + 16.3 = 27.3 Equation 2
5x — 2y = 5 Equation 1
2x + y + 16.3 — 16.3 = 27.3 — 16.3 Equation 2
5x — 2y = 5 Equation 1
2x + y = 11 Equation 2
2x + y = 11 We use the substitution method.
2x + y — 2x = 11 — 2x We express y in terms of x from Equation 2:
y = —2x + 11 Equation 3
5x — 2(—2x + 11) = 5 Substitute Equation 3 into Equation 1:
5x + 4x — 22 = 5
9x — 22 = 5
9x — 22 + 22 = 5 + 22 We determines x:
9x = 27
\(\frac{9 x}{9}\) = \(\frac{27}{9}\)
x = 3
y = —2(3) + 11 Substitute 3 for x in Equation 3:
= -6 + 11
= 5
x = 3 The system’s solution is:
y = 4
AB = AC = x + 5 = 3 + 5 = 8 We determine AB and AC:
BC = y + 6.3 = 5 + 6.3 = 11.3 We determine BC:
x = 3; y = 5
AB = 8 inches; AC = 8 inches BC = 11.3 inches
Question 23.
A bus company requires 4 buses and 8 vans to take 240 school children to the library. It requires 2 buses and 9 vans to take 170 children to the museum. Calculate the number of children a bus can carry and the number of children a van can carry.
Answer:
Let’s note:
b = the number of children in a bus
v = the number of children in a van
4b + 8v = 240 Equation 1
26 + 9v = 170 Equation 2
We write the system of equations:
2(2b + 9v) = 2(170) We use the elimination method.
4b + 18v = 340 Equation 3 Multiply Equation 2 by 2:
(4b + 18v) — (4b + 8v) = 340 — 240 Subtract Equation 1 from Equation 3:
4b + 18v — 4b — 8v = 100 Simplify:
10v = 100
\(\frac{10 v}{10}\) = \(\frac{100}{10}\) Divide by 10 and simplify:
v = 10
2b + 9(10) = 170 Substitute 10 for v in Equation 2:
2b + 90 = 170
2b + 90 — 90 = 170 — 90 Subtract 90 from both sides:
2b = 80
\(\frac{2 b}{2}\) = \(\frac{80}{2}\) Divide both sides by 2:
b = 40 Simplify:
A bus can carry 40 children, while a van can carry 10 children.
Bus: 40 children
Van : 10 children
Question 24.
At noon, Balloon M is 60 meters above ground, and Balloon N is 50 meters above ground. Balloon M is rising at the rate of 10 meters per second, while Balloon N is rising at the rate of 15 meters per second.
a) Write a system of two linear equations in which each equation gives the height, h meters, of a balloon t seconds after noon. Then solve the system using a graphing calculator.
Answer:
h = 60 + 10t Equation 1 a) We write a system of equations giving the height of each balloon:
h = 50 + 15t Equation 2
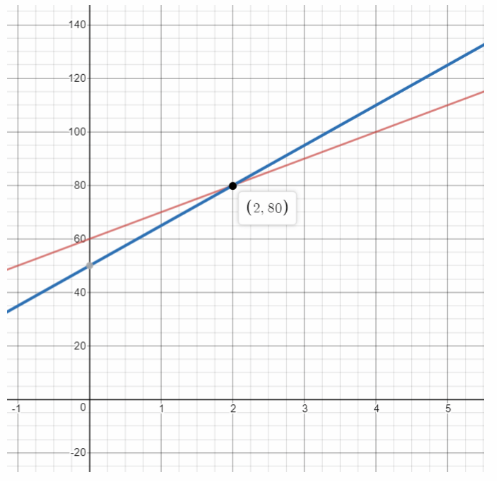
We use a graphing calculator to solve the system:
t = 2 The solution is:
h = 80
b) How many seconds after noon will the two balloons be at the same height?
How do you know?
Answer:
t = 2 seconds b) The two balloons will be at the same height when h = 80. We determined the time when this happens, which is the t-coordinate of the solution above:
a) t = 2, h = 80
b) 2 seconds
Question 25.
The water levels in two identical tanks rise at a rate of 4 inches per second. The water level, h inches, in Tank A is 3 inches at t = 0. The water level in Tank B is 16 inches at t = 3 seconds.
a) Write a system of equations for the water level h in the two tanks in terms of t.
Answer:
h = 3 + 4t Equation 1 a) we write system of equations for the water level in the two tanks
h = 16 + 4(t – 3) Equation 2
b) Graph the two equations on the same coordinate plane. Use 1 grid square on both axes to represent 1 unit for the interval 0 to 10.
Answer:
h = 4t + 3 Equation 1 b) We write the equations in slope-Intercept form
h = 16 + 4t – 12 Equation 2
h = 4t + 3 Equation 1
h = 4t + 4 Equation 2
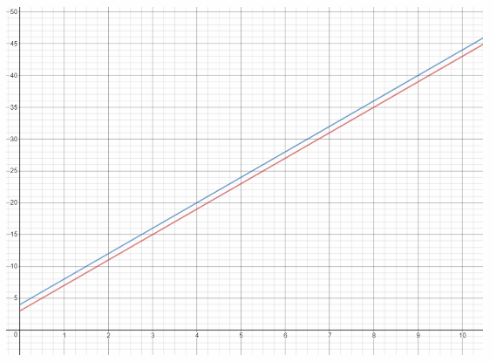
We graph the two equations the first has slope 4 and y-Intercept 3, while the second has slope 4 and y-intercept 4.
c) When will the two tanks have the same water level? How do you know?
Answer:
The two tanks will never have the same level because the system of equations in part (a) is inconsistent because the slope is the same, but the y-intercept is not
a)
h = 3 + 4t
h = 16 + 4(t — 3)
b) See graph
c) Never
Question 26.
Natalie has x bags of onions and y bags of potatoes. There are a total of 8 bags. Each bag weighs 2 pounds. The total weight of the bags is 16 pounds. She wants to find the value of x and y.
a) Write a system of two linear equations.
Answer:
x + y = 8 Equation 1
2x + 2y = 16 Equation 2
a) We write a system of equations:
b) State with reasons whether the system of equations has a unique solution, is inconsistent, or is dependent.
Answer:
\(\frac{1}{2}\) = \(\frac{1}{2}\) = \(\frac{8}{16}\) b) We notice that the coefficients of the variables and the constants are proportional:
This means that the system is dependent
c) Can Natalie find the value of x and y? Why?
Answer:
She cannot find the value of x and y because there are an infinity of solutions.
a)
x + y = 8
2x + 2y = 16
b) Dependent system
c) No