Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 5 Lesson 5.5 Inconsistent and Dependent Systems of Linear Equations to score better marks in the exam.
Math in Focus Grade 7 Course 3 A Chapter 5 Lesson 5.5 Answer Key Inconsistent and Dependent Systems of Linear Equations
Math in Focus Grade 8 Chapter 5 Lesson 5.5 Guided Practice Answer Key
Identify whether each system of linear equations is inconsistent or has a unique solution. Justify your reasoning.
Question 1.
11x + y = 2 — Equation 1
22x + 2y = 3 —Equation 2
Rewrite each linear equations in slope-intercept form y = mx + b.
Equation 1
11x + y = 2
![]() =
= ![]() Subtract 11x from both sides.
Subtract 11x from both sides.
y = ![]() Simplify.
Simplify.
Equation 2
22x + 2y = 3
![]() =
= ![]() Subtract 22x from both sides.
Subtract 22x from both sides.
![]() =
= ![]() Simplify.
Simplify.
![]() =
= ![]() Divide both sides by 2.
Divide both sides by 2.
y = ![]() Simplify.
Simplify.
The slope of the graph of the Equation 1 is ![]() and the y-intercept is
and the y-intercept is ![]() .
.
The slope of the graph of the Equation 2 is ![]() and the y-intercept is
and the y-intercept is ![]() .
.
The graphs of the linear equations have the same ![]() and different
and different ![]() . The system of linear equations is
. The system of linear equations is ![]() , because the system of linear equations has no solution.
, because the system of linear equations has no solution.
Answer:
11x + y = 2 Equation 1 We are given the system of equations:
22x + 2y = 3 Equation 2
11x + y = 2 Rewrite Equation 1 in slope-intercept form y = mx + b:
11x + y — 11x = 2 — 11x Subtract 11x from both sides:
y = —11x + 2 Simplify:
22x + 2y = 3 Rewrite Equation 2 in slope-intercept form y = mx + b
22x + 2y — 22x = 3 — 22x Subtract 22x from both sides
2y = —22x + 3 Simplify:
\(\frac{2 y}{2}\) = \(\frac{-22 x+3}{2}\) Divide both sides by 2:
y = -11x + \(\frac{3}{2}\) Simplify:
The slope of the graph of Equation 1 is -11 and the y-intercept is 2.
The slope of the graph of Equation 2 is -11 and the y-intercept is \(\frac{3}{2}\).
The graphs of the linear equations have the same slope and different y-intercept. The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent
Question 2.
13x + y = 23
26x + 2y = 21
Answer:
13x + y = 23 Equation 1 We are given the system of equations:
26x + 2y = 21 Equation 2
13x + y = 23 Rewrite Equation 1 in slope-intercept form y = mx + b:
13x + y — 13x = 23 — 13x Subtract 13x from both sides
y = —13x -i- 23 Simplify:
26x + 2y = 21 Rewrite Equation 2 in slope-intercept form y = mx + b:
26x + 2y — 26x = 21 — 26x Subtract 26x from both sides:
2y = -26x + 21 Simplify:
\(\frac{2 y}{2}\) = \(\frac{-26 x+21}{2}\) Divide both sides by 2:
y = —13x + \(\frac{21}{2}\) Simplify:
The slope of the graph of Equation 1 is -13 and the gj-intercept is 23.
The slope of the graph of Equation 2 is -13 and the y-intercept is \(\frac{21}{2}\).
The graphs of the linear equations have the same slope and different y-intercept The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent
Question 3.
\(\frac{1}{2}\)x + y = 4
3x + 8y = 16
Answer:
\(\frac{1}{4}\)x + y = 4 Equation 1
3x + 8y = 16 Equation 2
We are given the system of equations:
\(\frac{1}{2}\)x + y = 4 Rewrite Equation 1 in slope-intercept form y = mx + b:
\(\frac{1}{2}\)x + y – \(\frac{1}{2}\)x = 4 – \(\frac{1}{2}\)x Subtract 11x from both sides:
y = – \(\frac{1}{2}\)x + 4 Simplify:
3x + 8 = 16 Rewrite Equation 2 in slope-intercept form y = mx + b:
3x + 8y — 3x = 16 — 3x Subtract 3x from both sides:
8y = —3x + 16 Simplify:
\(\frac{8 y}{8}\) = \(\frac{-3 x+16}{8}\) Divide both sides by 8:
y = \(-\frac{3}{8}\)x + 2 simplify
The slope of the graph of Equation 1 is – \(\frac{1}{2}\) and the y-intercept is 4.
The slope of the graph of Equation 2 is – \(\frac{3}{8}\) and the y-intercept is 2.
– \(\frac{1}{2}\)x + 4 = — \(\frac{3}{8}\) + 2 The graphs of the linear equations have different slopes, therefore tne system of linear equations has a unique solution.
8 ∙ (-\(\frac{1}{2}\)x + 4) = 8 ∙ (-\(\frac{3}{8}\)x + 2
—4x + 32 = -3x + 16
-4x + 32 + 4x = -3x + 16 + 4x
32 = x + 16
32 — 16 = x + 16 — 16
x = 16
y = –\(\frac{3}{8}\)(16) + 2
= -6 + 2
= -4
Unique solution (x = 16; y = -4)
Question 4.
\(\frac{1}{3}\)x + y = 7
x + 3y = 6
Answer:
\(\frac{1}{3}\)x + y = 7 Equation 1
x + 3y = 6 Equation 2
We are given the system of equations:
\(\frac{1}{3}\)x + y = 7 Rewrite Equation lin slope-intercept form y = mx + b:
\(\frac{1}{3}\)x + y – \(\frac{1}{3}\)x = 7 – \(\frac{1}{3}\)x Subtract \(\frac{1}{3}\)x from both sides:
y = –\(\frac{1}{3}\)x + 7 Simplify:
x + 3y = 6 Rewrite Equation 2 in slope-intercept form y = mx + b:
x + 3y — x = 6 — x Subtract x from both sides:
3y = —x + 6 Simplify:
\(\frac{3 y}{3}\) = \(\frac{-x+6}{3}\) Divide both sides by 3:
y = \(\frac{1}{3}\)x + 2 Simplify:
The slope of the graph of Equation 1 is —\(\frac{1}{3}\) and the y-intercept is 7
The slope of the graph of Equation 2 is –\(\frac{1}{3}\) and the y-irtercept is 2.
The graphs of the linear equations have the same slope and different y-intercept The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent
Identify whether the system of linear equations is inconsistent or has a unique solution. Justify your reasoning.
Question 5.
5x + 2y = 4
20x + 8y = 30
Answer:
5x + 2y = 4 Equation 1
20x + 8y = 30 Equation 2
We are given the system of equations:
5x + 2 = Rewrite Equation 1 in slope-intercept form y = mx + b:
5x + 2y — 5x = 4 — 5x Subtract 5x from both sides and simplify:
\(\frac{2 y}{2}\) = \(\frac{-5 x+4}{2}\)
y = \(-\frac{5}{2}\)x + 2 Divide both sides by 2 and simplify:
20x + 8y = 30 Rewrite Equation 2 in slope-intercept form y = mx + b:
20x + 8y – 20x = 30 — 20x Subtract 20x from both sides and simplify:
8y = -20x + 30
\(\frac{8 y}{8}\) = \(\frac{-20 x+30}{8}\) Divide both sides by 8 and simplify:
y = –\(\frac{5}{2}\)x + \(\frac{15}{4}\)
The slope of the graph of Equation 1 is –\(\frac{5}{2}\) and the y-intercept is 2.
The slope of the graph of Equation 2 is —\(\frac{5}{2}\) and the y-intercept is \(\frac{15}{4}\).
The graphs of the linear equations have the same slope and different y-intercept The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent
Question 6.
7x + y = 14
10x + 4y = 32
Answer:
7x + y = 14 Equation 1 We are given the system of equations
10x + 4y = 32 Equation 2
7x + 4y = 14 Rewrite Equation 1 in slope-Intercept form y = mx + b
7x + y — 7x = 14 — 7x subtract 7x from both sides and simplify
y = —7x + 14 simplify
10x + 4y = 32 Rewrite Equation 2 in slope-intercept form y = mx + b
10x + 4y – 10x = 32 — 10x Subtract 10x from both sides and simplify:
4y = -10x + 32 simplify
\(\frac{4 y}{2}\) = \(\frac{-10 x+32}{4}\) Divide both sides by 4
y = –\(\frac{5}{2}\)x + 8 Simplify:
The slope of the graph of Equation 1 is -7 and the y-intercept is 14.
The slope of the graph of Equation 2 is –\(\frac{5}{2}\) and the y-intercept is 8.
—7x + 14 = —\(\frac{5}{2}\)x + 8 The graphs of the linear equations have different slopes, therefore the system of linear equations has an unique solution.
2 ∙ (-7x + 14) = 2(-\(\frac{5}{2}\)x + 8)
—14x + 28 = —5x + 16
—14x + 28 + 14x = —5x + 16 + 14x
28 = 9x + 16
28 — 16 = 9x + 16 — 16
12 = 9x
\(\frac{12}{9}\) = \(\frac{9 x}{9}\)
x = \(\frac{4}{3}\)
y = –\(\frac{5}{2}\) ∙ \(\frac{4}{3}\) + 8
= –\(\frac{10}{3}\) + 8
= \(\frac{14}{3}\)
Unique solution (x = \(\frac{4}{3}\); y = \(\frac{14}{3}\))
Question 7.
12x + 4y = 16
9x + 3y = 12
Answer:
12x + 4y = 16 Equation 1
9x + 3y = 12 Equation 2
we are given the system of equations:
12x + 4y = 16 Rewrite Equation 1 in slope-intercept form y = mx + b:
12x + 4y — 12x = 16 — 2x Subtract 12x from both sides and simplify:
4y = —12x + 16
\(\frac{4 y}{4}\) = \(\frac{-12 x+16}{4}\) Divide both sides by 4 and simplify:
y = —3x + 4
9x + 3y = 12 Rewrite Equation 2 in slope-intercept form y = mx + b:
9x + 3y — 9x = 12 — 9x Subtract 9x from both sides and simplify:
3y = —9x + 12
\(\frac{3 y}{4}\) = \(\frac{-9 x+12}{3}\) Divide both sides by 3 and simplify:
y = -3x + 4
Since Equation 1 and Equation 2 are equivalent, they have an infinite number of solutions. Therefore system of linear equations is dependent.
Dependent
Math in Focus Course 3A Practice 5.5 Answer Key
Graph each system of linear equations using a graphing calculator. State whether each system of equations is inconsistent or has a unique solution.
Question 1.
3x + y = 4
6x + 2y = 14
Answer:
3x + y = 4 Equation 1 We are given the system of equations:
6x + 2y = 14 Equation 2
3x + = 4 Rewrite Equation 1 in slope-intercept form y = mx + b:
3x + y — 3x = 4 — 3x Subtract 3x from both sides:
y = —3x + 4 Simplify:
6x + 2y = 14 Rewrite Equation 2 in slope-intercept form y = mx + b:
6x + 2y — 6x = 14 — 6x Subtract 6x from both sides:
2y = —6x + 14 Simplify:
\(\frac{2 y}{2}\) = \(\frac{-6 x+14}{2}\) Divide both sides by 2:
y = -3x + 7 Simplify:
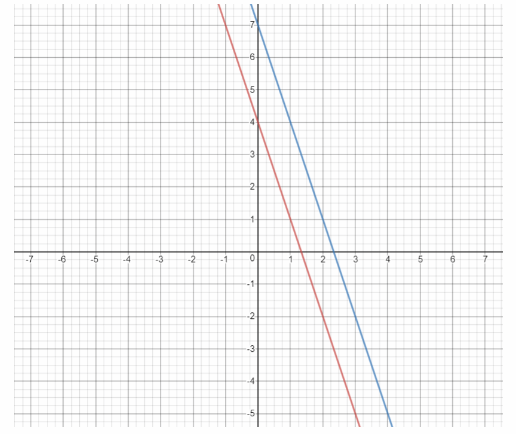
We graph the two equations using a graphing calculator:
The graphs of the linear equations are parallel tines, so there is no point of intersection. Since there are no points that lie on both graphs, the system of linear equations is inconsistent
Inconsistent
Question 2.
10x + 5y = 15
x + y = 3
Answer:
10x + 5y = 15 Equation 1
x + y = 3 Equation 2
We are given the system of equations:
10x + 5y = 15 Rewrite Equation 1 in slope-intercept form y = mx + b:
10x + 5y — 10x = 15 — 10x Subtract 10x from both sides and simplify:
5y = 15 — 10x
\(\frac{5 y}{5}\) = \(\frac{-10 x+15}{5}\) Divide by 5 and simplify:
y = —2x + 3 Rewrite Equation 2 in slope-intercept form y = mx + b:
x + y — x = 3 — x Subtract x from both sides and simplify:
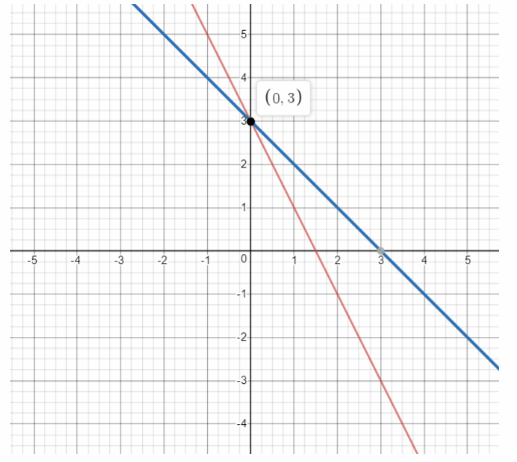
We graph the two equations:
x = 0
The graphs intersect in the point (0, 3). The system of linear equations has an unique solution:
y = 3
Unique solution (x = 0, y = 3)
Question 3.
x – 2y = 14
4y = 5 + 2x
Answer:
x — 2y = 14 Equation 1
4y = 5 + 2x Equation 2
We are given the system of equations:
x — 2y = 11 Rewrite Equation 1 in slope-intercept form y = mx + b:
x — 2y — x = 14 — x Subtract x from both sides and simplify:
-2y = 14 – x
\(\frac{-2 y}{-2}\) = \(\frac{14-x}{-2}\) Divide by -2 and simplify:
y = \(\frac{1}{2}\)x – 7
Divide by -2 and simplify:
4y = 5 + 2x Rewrite Equation 2 in slope-intercept form y = mx + b:
\(\frac{4 y}{4}\) = \(\frac{2 x+5}{4}\) Divide both sides by 4 and simplify:
y = \(\frac{1}{2}\)x + \(\frac{5}{4}\)
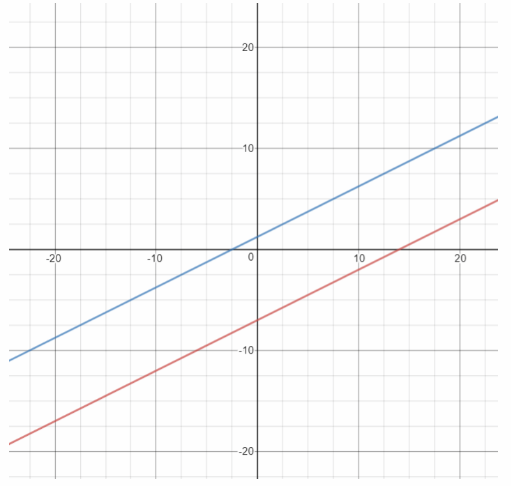
Graph both equations using a graphing calculator:
The graphs of the linear equations are parallel therefore there is no point to lie on both graphs, so the system has no solution, it is inconsistent.
Inconsistent
State whether each system of linear equations is inconsistent, dependent, or has a unique solution. Justify each answer. Solve each system of linear equations if possible.
Question 4.
x + y = 3
8x + 8y = 32
Answer:
x + y = 3 Equation 1
8x + 8y = 32 Equation 2
We are given the system of equations:
x + y = 3 Rewrite Equation 1 in slope-intercept form y = mx + b:
x + y — x = 3 — x Subtract x from both sides and simplify:
y = -x + 3
8x + 8y = 32 Rewrite Equation 2 in slope-intercept form y = mx + b:
8x + 8y — 8x = 32 — 8x Subtract 8x from both sides and simplify:
\(\frac{8 y}{8}\) = \(\frac{-8 x+32}{8}\) Divide both sides by 8 and simplify:
y = -x + 4
The linear equations have the same slope and different y-intercept The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent
Question 5.
6x + 2y = 12
3x + y = 21
Answer:
6x + 2y = 12 Equation 1
3x + y = 21 Equation 2
We are given the system of equations:
6x + 2y = 12 Rewrite Equation 1 in slope-intercept form y = mx + b:
6x + 2y — 6x = 12 — 6x Subtract 6x from both sides and simplify:
2y = —6x + 12
\(\frac{2 y}{2}\) = \(\frac{-6 x+12}{2}\) Divide both sides by 2 and simplify:
y = —3x + 6
3x + y = 21 Rewrite Equation 2 in slope-intercept form y = mx + b
3x + y – 3x = 21 – 3x Subtract 3x from both sides and simplify
y = -3x + 21
The linear equations have the same slope and different y-Intercept. The system of linear equations is Inconsistent because the system of linear equations has no solution.
Inconsistent
Question 6.
3x – 6y = 12
x – 2y = 4
Answer:
3x — 6y = 12 Equation 1
x — 2y = 4 Equation 2
We are given the system of equations:
3x – 6y = 12 Rewrite Equation 1 in slope-intercept form y = mx + b:
3x — 6y — 3x = 12 — 3x Subtract 3x from both sides and simplify:
—6y = —3x + 12
\(\frac{-6 y}{-6}\) = \(\frac{-3 x+12}{-6}\) Divide both sides by -6 and simplify:
y = \(\frac{1}{2}\)x – 2
x – 2y = 4 Rewrite Equation 2 in slope-intercept form y = mx + b:
x — 2y — x = 4 — x Subtract x from both sides and simplify:
—2y = —x + 4
\(\frac{-2 y}{-2}\) = \(\frac{-x+4}{-2}\) Divide both sides by -2 and simplify:
y = \(\frac{1}{2}\)x – 2
Since Equation 1 and Equation 2 are equivalent, they have an infinite number of solutions.
Therefore system of linear equations is dependent
Dependent
Question 7.
-15x + 3y = 3
-5x + y = 21
Answer:
—15x + 3y = 3 Equation 1
—5x + y = 21 Equation 2
We are given the system of equations:
-15x + 3y = 3 Rewrite Equation 1 in slope-intercept form y = mx + b:
—15x + 3y — 15x = 3 + 15x Add 15x to both sides and simplify
3y = 15x + 3
\(\frac{3 y}{3}\) = \(\frac{15 x+3}{3}\) Divide both sides by 3 and simplify:
y = 5x + 1
-5x + y = 21 Rewrite Equation 2 in slope-intercept form y = mx + b:
—5x + y + 5x = 21 + 5x Add 5x to both sides and simplify:
y = 5x + 21
The linear equations have the same slope and different y-intercept. The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent
Question 8.
2x + y = 8
4x – 2y = 24
Answer:
2x + y = 8 Equat ion 1
4x – 2y = 24 Equation 2
We are given the system of equations:
2x + y = 8 Rewrite Equation 1 in slope-intercept form y = mx + b:
2x + y — 2x = 8 — 2x Subtract 2x from both sides and simplify:
y = —2x + 8
4x — 2y = 24 Rewrite Equation 2 in slope-intercept form y = mx + b:
4x — 2y — 4x = 24 — 4x Subtract 4x from both sides and simplify:
—2y = —4x + 24
\(\frac{-2 y}{-2}\) = \(\frac{-4 x+24}{-2}\) Divide both sides by -2 and simplify:
y = 2x — 12
The slope of the graph of Equation 1 is -2 and the y-intercept is 8.
The slope of the graph of Equation 2 is 2 and the y-intercept is —12.
—2x + 8 = 2x — 12 The graphs of the linear equations have different slopes, therefore the system of linear equations has an unique solution.
—2x + 8 + 2x = 2x – 12 + 2x
8 = 4x — 12
8 + 12 = 4x — 12 + 12
4x = 20
x = \(\frac{20}{4}\)
x = 5
y = -2(5) + 8
= —10+8
= -2
Unique solution (x = 5; y = -2)
Question 9.
8x + 7y = 9
40x + 35y = 45
Answer:
8x + 7y = 9 Equation 1
40x + 35y = 45 Equation 2
We are given the system of equations:
8x + 7y = 9 Rewrite Equation 1 in slope-intercept form y = mx + b:
8x + 7y – 8x = 9 — 8x Subtract 8x from both sides and simplify:
7y = -8x + 9
\(\frac{7 y}{7}\) = \(\frac{-8 x+9}{7}\)
y = –\(\frac{8}{7}\)x + \(\frac{9}{7}\) Divide both sides by 7 and simplify:
40x + 35y = 45 Rewrite Equation 2 in slope-intercept form y = mx + b:
40x + 35y — 40x = 45 — 40x Subtract 40 from both sides and simplify:
35y = —40x + 45
\(\frac{35 y}{35}\) = \(\frac{-40 x+45}{35}\) Divide both sides by 35 and simpbfy:
y = –\(\frac{8}{7}\)x + \(\frac{9}{7}\)x
Since Equation 1 and Equation 2 are equivalent, they have an infinite number of solutions. Therefore system of linear equations is dependent
Dependent
Question 10.
x + 3y = 9
2x + 6y = 5
Answer:
x + 3y = 9 Equation 1
2x + 6y = 5 Equation 2
We are given the system of equations:
x + 3y = 9 Rewrite Equation 1 in slope-intercept form y = mx + b:
x + 3y — x = 9 — x Subtract x from both sides and simplify:
\(\frac{3 y}{3}\) = \(\frac{-x+9}{3}\) Divide both sides by 3 and simplify:
y = \(-\frac{1}{3} x\) + 3
2x + 6y = 6
Rewrite Equation 2 in slope-intercept form y = mx + b:
2x + 6y — 2x = 5 — 2x Subtract 2x from both sides and simplify:
6y = —2x + 5
\(\frac{6 y}{6}\) = \(\frac{-2 x+5}{6}\) Divide both sides by 6 and simplify:
y = –\(\frac{1}{3} x\) + \(\frac{5}{6}\)
The linear equations have the same slope and different y-intercept. The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent
Question 11.
9x + 21y = 27
6x + 14y = 18
Answer:
9x + 21y = 27 Equation 1
6x + 14y = 18 Equation 2
We are given the system of equations:
9x + 21y = 27 Rewrite Equation 1 in slope-intercept form y = mx + b:
9x + 21y – 9x = 27 — 9x Subtract 9x from both sides and simplify:
21y = —9x + 27
\(\frac{21 y}{21}\) = \(\frac{-9 x+27}{21}\) Divide both sides by 21 and simplify:
y = \(-\frac{3}{7}\)x + \(\frac{9}{7}\)
6x + 14y = 18 Rewrite Equation 2 in slope-intercept form y = mx + b
6x + 14y — 6x = 18 — 6x Subtract 6x from both sides and simplify:
14y = —6x + 18
\(\frac{14 y}{14}\) = \(\frac{-6 x+18}{14}\) Divide both sides by 14 and simplify:
y = \(-\frac{3}{7}\) + \(\frac{9}{7}\)
Since Equation 1 and Equation 2 are equivalent, they have an infinite number of solutions.
Therefore system of linear equations is dependent
Dependent
Question 12.
5x + 4y = 6
15x + 12y = 18
Answer:
5x + 4y = 6 Equation 1
15x + 12y = 18 Equation 2
We are given the system of equations:
5x + 4y = 6 Rewrite Equation 1 in slope-intercept form y = mx + b:
5x + 4y — 5x = 6 — 5x Subtract 4x from both sides and simplify:
4y = -5x + 6
\(\frac{4 y}{4}\) = \(\frac{-5 x+6}{4}\) Divide both sides by 5 and simplify:
y = \(-\frac{5}{4}\)x + \(\frac{3}{2}\)
15x + 12y = 18 Rewrite Equation 2 in slope-intercept form y = mx + b:
15x + 12y — 15x = 18 — 15x Subtract 15x from both sides and simplify:
12y = -15x + 18
\(\frac{12 y}{12}\) = \(\frac{-15 x+18}{12}\) Divide both sides by 12 and simplify:
y = \(-\frac{5}{4}\)x + \(\frac{3}{2}\)
Since Equation 1 and Equation 2 are equivalent, they have an infinite number of solutions.
Therefore system of linear equations is dependent
Dependent
Solve. Show your work.
Question 13.
David says he bought 9 apples and 6 apricots for $8.50 yesterday and bought 3 apples and 2 apricots for $7.40 today.

a) Write a system of equations to find the cost of an apple and an apricot.
Answer:
9x + 6y = 8.50 Equation 1
3x + 2y = 7.40 Equation 2
a) Lets note:
x = the cost of an apple
y = the cost of an apricot
We can write the system of equations:
b) State with reasons whether the system of equations has a unique solution, is inconsistent, or is dependent.
Answer:
9x + 6y = 8.50 b) Rewrite Equation 1 in slope-intercept form y = mx + b
9x + 6y — 9x = 8.50 – 9x Subtract 9x from both sides and simplify:
6y = -9x + 8.50
\(\frac{6 y}{6}\) = \(\frac{-9 x+8.50}{6}\) Divide both sides by 6 and simplify:
y = \(-\frac{3}{2}\)x + \(\frac{4.25}{3}\)
3x + 2y = 7.40 Rewrite Equation 2 in slope-intercept form y = mx + b:
3x + 2y — 3x = 7.40 — 3x Subtract 3x from both sides and simplify:
2y = 7.40 — 3x
\(\frac{2 y}{2}\) = \(\frac{-3 x+7.40}{2}\) Divide both sides by 2 and simplify:
y = –\(\frac{3}{2}\) + 3.70
The linear equations have the same slope and different y-intercept. The system of linear equations is inconsistent because the system of linear equations has no solution.

c) What does this tell you about the cost of apples and apricots on those two days?
Answer:
The cost of at least one type of fruits is different in the two days.
a) 9x + 6y = 8.50
3x + 2y = 7.40
b) Inconsistent system
c) The unit price changed
Question 14.
Ms. Cohen gave a riddle: A string is 2 meters longer than a rod. Half of the rod is 1 meter shorter than half of the string. Is this true or false?
a) Write a system of equations to find the length of the string and the length of the rod.
Answer:
s = r + 2 Equation 1
\(\frac{1}{2}\)r = \(\frac{1}{2}\)s – 1 Equation 2
(a) Let’s note:
s=the length of a string
r=the length of a rod
We can write the system of equations:
b) State with reasons whether the system of equations has a unique solution, is inconsistent, or is dependent.
Answer:
s = r + 2 b) Equation 1 is in slope-intercept form:
2 • \(\frac{1}{2}\)r = 2 • (\(\frac{1}{2}\)s – 1) We write Equation 2 in slope-intercept form:
r = s – 2
r + 2 = s – 2 + 2
s = r + 2
The two equations are equivalent therefore the system of equations is dependent and it has an infinity of solutions.
c) Comment on Ms. Cohen’s riddle.
Answer:
The answer ‘false’ to the question aims the situation in which the system is inconsistent while the answer ‘true’ reflects the cases in which the system either has a solution, or is dependent
a)
s = r + 2
\(\frac{1}{2}\)r = \(\frac{1}{2}\)s – 1
b) dependent system
c)The riddle is true as the system nas an infinity of solutions.
Question 15.
Math Journal Mr. Braunstein uses a cell phone plan that charges 2¢ per minute for local calls and 3.5¢ per minute for long distance calls. He made x minutes of local calls and y minutes of long distance calls in June. In July, he made 2x minutes of local calls and 2y minutes of long distance calls. His bill was $12 in June and $24 in July. Can he find how many minutes of each type of call he made each month? Explain.
Answer:
0.02x + 0.035y = 12 Equation 1
0.02(2x) + 0.035(2y) = 24 Equation 2
We write the system of equations:
All the coefficients of the two equations and the constants on the right are proportional, therefore the system is dependent which means the system has infinitely many solutions. This means he cannot find how many minutes of each type of call he made each month.
No (dependent system of equations)
Brain @ Work
Question 1.
Lorraine has $110 and Jane has $600 in their bank accounts. Lorraine’s account balance increases by $30 every year and her account balance will be C dollars in x years. Jane’s account balance reduces by $40 every year and her account balance will also be C dollars in x years.
a) Write two equations of C in terms of x.
Answer:
C = 110 + 30x
a) We write an equation for Lorraine account:
C = 600 — 40x We write an equation for Janes account:
b) Solve this system of linear equations to find the amount in the girls’ account balances when they are equal.
Answer:
C = 110 + 30x Equation 1 b) We write the system of equations:
C = 600 — 40x Equation 2
110 + 30x = 600 — 40x We substitute Equation 1 in Equation 2 and determine x:
110 + 30x + 40x = 600 — 40x + 40x
110 + 70x = 600
110 + 70x — 110 = 600— 110
70x = 490
x = \(\frac{490}{70}\)
x = 7
C = 110 + 30(7) Substitute 7 for c in Equation 1 to determine C:
= 110+ 210
= 320
a) C = 110 + 30x ; C = 110 + 30x
b) $320
Question 2.
The diagram below shows a 1-centimeter block of metals A and B.
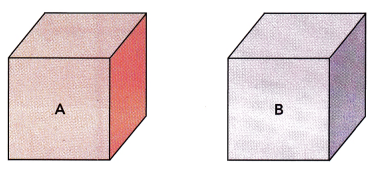
Five blocks of A and two blocks of B have a total mass of 44 grams. Three blocks of A and five blocks of B have a total mass of 34 grams. An alloy is made by melting and mixing two blocks of metal A and one block of metal B.
![]()
Answer:
Lets note:
a = the mass of an A bIock
b = the mass of a B block
5a + 2b = 44 Equation 1
3a + 5b = 34 Equation 2
We write the system of equations:
5(5a + 2b) 5(44) Multiply Equation 1 by 5:
25a + 10b = 220 Equation 3
2(3a + 5b) = 2(34) Multiply Equation 2 by 2:
6a + 10b = 68 Equation 4 from Equation 3:
(25a + 10b) – (6a + 10b) = 220 — 68 we subtract Equation 4 from Equation 3:
25a + 10b — 6a — 1ob = 152 Simplify:
19a = 152
\(\frac{19 a}{19}\) = \(\frac{152}{19}\) We divide both sides by 19 and simplify:
a = 8
5(8) + 2b = 44 Substitute 8 for a in Equation 1 to determine b:
40 + 2b = 44
40 + 2b — 40 = 44 — 40
2b = 4
\(\frac{2 b}{2}\) = \(\frac{4}{2}\)
b = 2
![]()
we determine the density of the alloy
= \(\frac{2(8)+2}{3}\) = \(\frac{18}{3}\)
= 6 grams/cm3
Question 3.
The table shows Joseph’s phone usage and the total charges over three months.
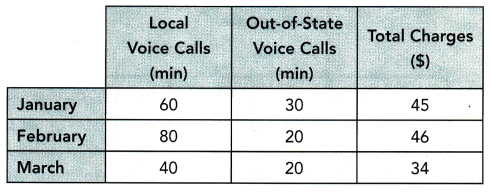
Joseph suspects that there are errors in the charges. Use systems of linear equations to check whether the charges are correct.
Answer:
Let’s note:
x = the cost of a minute of a local voice call
y = the cost of one minute of an cut-of-state voice call
\(\frac{60}{40}\) = \(\frac{30}{20}\) ≠ \(\frac{45}{34}\) We notice that then coefficients of the variables for January and March are proportional, but the constants are not:
60x + 30y = 45 Equation 1
40x + 20y = 34 Equation 2
This means that the system of equations corresponding to these months is inconsistent
Therefore there is no solution, which is not correct: the charges for at least one of the months January and March is wrong
Incorrect