Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 5 Lesson 5.4 Solve Systems of Linear Equations by Graphing to score better marks in the exam.
Math in Focus Grade 7 Course 3 A Chapter 5 Lesson 5.4 Answer Key Solve Systems of Linear Equations by Graphing
Math in Focus Grade 8 Chapter 5 Lesson 5.4 Guided Practice Answer Key
Technology Activity
Materials:
- graphing calculator
Explore The Graphical Method
Work in pairs.
Step 1.
Solve the system of linear equations using the elimination method or substitution method.
x + 2y = 4
x – y = 1
Step 2.
To solve this system of linear equations using a graphing calculator, solve each equation for y and enter each expression for y into the calculator.
Step 3.
Press the key. Use the function and select 5:lntersect to find
where the two graphs intersect.
Caution
Be sure to use parentheses around any fractional coefficients, and use the ![]() key if the coefficient is negative.
key if the coefficient is negative.
Step 4.
Repeat step 1 to step 3 for the system of linear equations
6x – 5y = -3,
x + y = 5.
Math Journal How is the solution you found in step 1 related to the coordinates of the point of intersection in step 3? Why do you think this happens?
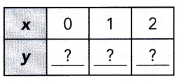
Solve using the graphical method. Copy and complete the tables of values. Graph the system of linear equations on the same coordinate plane. Use 1 grid square on both axes to represent 1 unit for the x interval from -1 to 3 and the y interval from -1 to 5.
Question 1.
2x + y = 5
x – y = -2
2x + y = 5
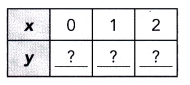
x – y = -2
From the graph, the slope of 2x + y = 5 is ![]() and the y-intercept is
and the y-intercept is ![]() . The slope of x – y = -2 is
. The slope of x – y = -2 is ![]() and its y-intercept is
and its y-intercept is ![]() .
.
The point of intersection is (![]() ,
, ![]() ). Therefore, the solution to the system of equations is x =
). Therefore, the solution to the system of equations is x = ![]() and y =
and y = ![]() .
.
Solve using the graphical method. Graph each system of linear equations on the same coordinate plane. Use 1 grid square on both axes to represent 1 unit for the Interval from -4 to 4.
Answer:
2x + y = 5
x – y = -2
We are given the system of equations:
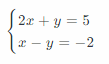
For the equation 2x + y = 5 we build the table of values:
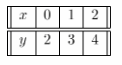
For the equation x – y = -2 we build the table of values:
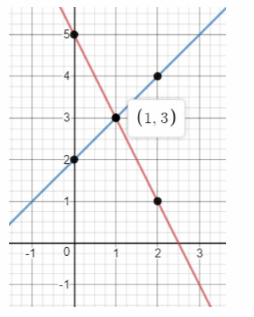
We graph the two lines:
From the graph, the slope of 2x + y = 5 is -2 and the y-Intercept is 5.
The slope of x – y = -2 is 1 and the y-Intercept is 2.
The point of intersection is (1, 3). Therefore the solution of the system of equations is x = 1 and y = 3.
x = 1; y = 3
Question 2.
x + 2y = 5
x + y = 2
Answer:
x + 2y = 5
x + y = 2
We are given the system of equations:
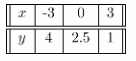
For the equation x + 2y = 5 we build the table of values:
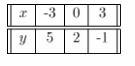
For the equation x + y = 2 we build the table of values:
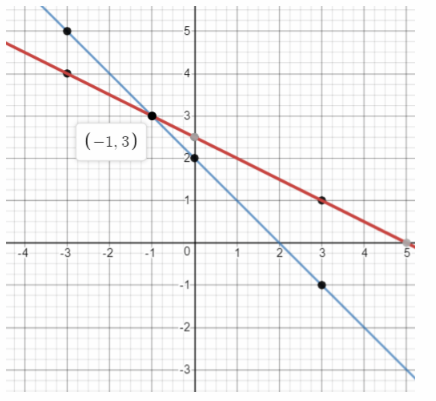
We graph the two lines:
From the graph, the slope of x + 2y = 5 is -0.5 and the y-Intercept is 2.5. The slope of x + y = 2 is -1 and the y-Intercept is 2.
The point of intersection is (-1, 3). Therefore the solution of the system of equations is x = -1 and y = 3.
x = -1; y = 3
Question 3.
3x + 2y = 8
x – y = 1
Answer:
3x + 2y = 8
x – y = 1
We are given the system of equations:
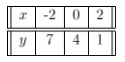
For the equation 3x + 2y = 8 we build the table of values:
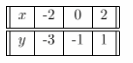
For the equation x – y = 1 we build the table of values:
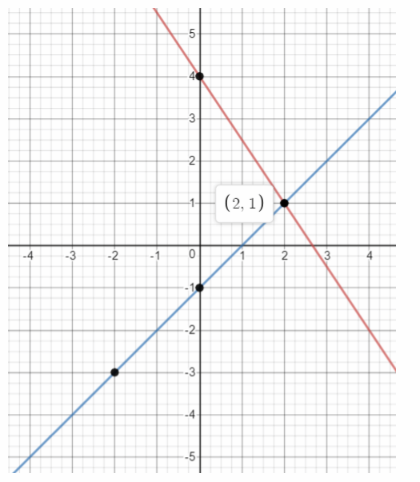
We graph the two lines:
From the graph, the slope of 3x + 2y = 8 is -1.5 and the y-Intercept is 4. The slope of x – y = 1 is 1 and the y-Intercept is -1.
The point of intersection is (2, 1). Therefore the solution of the system of equations is x = 2 and y = 1.
x = 2; y = 1
Use graph paper. Use 1 grid square on both axis to represent 10 seconds for the t interval from 110 to 150 seconds, and 10°F for the T interval from 300 to 350°F.
Question 4.
Two ovens are being heated. Their temperatures are represented by the equations
Oven 1: T = t + 200
Oven 2: T = 2t + 80
where T is the temperature in °F of the oven and t is the time in seconds. Solve the system of linear equations graphically. When will the temperatures of the ovens be the same?
Answer:
T = t + 200
T = 2t + 80
We are given the system of equations:
For the equation T = t + 200 the slope is 1 and the y-intercept is 200.
For the equation T = 2t + 80 the slope is 2 and the y-intercept is 80.
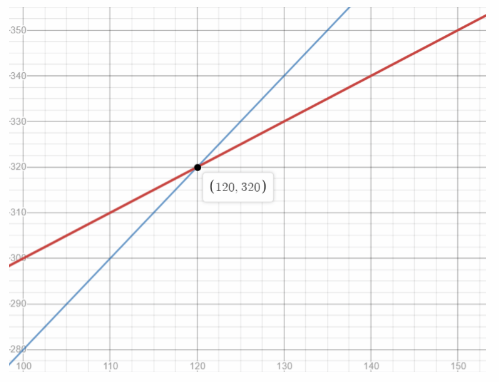
We sketch the graph of the two equations using the slope and the y-irtercept values:
The point of intersection is (120, 320). Therefore the solution of the system of equations is t = 120 and T = 320.
t = 120 seconds; T = 320° F
Math in Focus Course 3A Practice 5.4 Answer Key
For this practice, unless otherwise stated, use 1 grid square to represent 1 unit on both axes for the interval from —8 to 8. Solve each system of linear equations using the graphical method.
Question 1.
x + y = 6
2x + y = 8
Answer:
x + y = 6
2x + y = 8
We are given the system of equations:
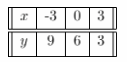
a) Copy and complete the tables of values for the system of linear equations, x + y = 6

Answer:
For the equation x + y = 6 we build the table of values:
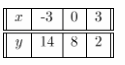
For the equation 2x + y = 8 we build the table of values:
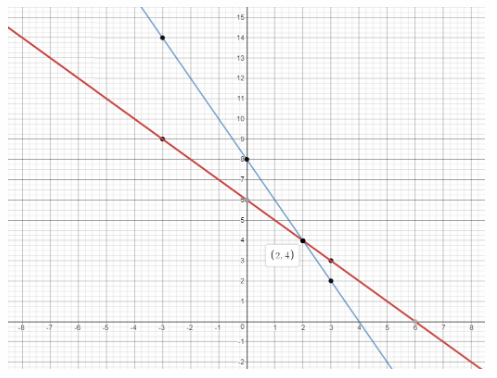
b) Graph x + y = 6 and 2x + y = 8 on the same coordinate plane. Find the point of intersection.
Answer:
We graph the two lines:
From the graph, the slope of x + y = 6 is -1 and the y-intercept is 6
The slope of 2x + y = 8 is -2 and the y-intercept is 8.
The point of intersection is (2, 4).
c) Use the graph in b) to solve the system of linear equations.
Answer:
Therefore the solution of the system or equations is x = 2 and y = 4.
x = 2; y = 4
Question 2.
x + y = 5
x – y = 2
a) Copy and complete the tables of values for the system of linear equations, x + y = 5

Answer:
x + y = 5
x – y = 2
We are given the system of equations:
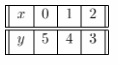
For the equation x + y = 5 we build the table of values:
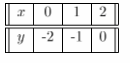
For the equation x – y = 2 we build the table of values:
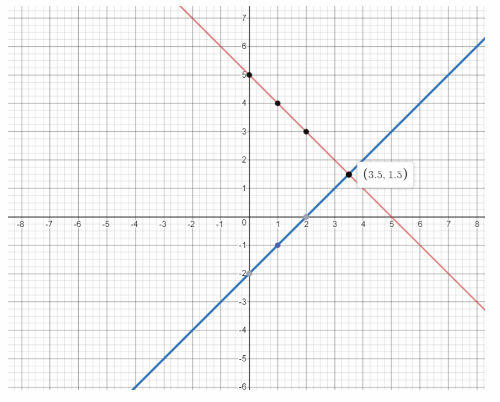
We graph the two lines:
b) Graph x + y = 5 and x — y = 2 on the same coordinate plane. Find the point of intersection.
Answer:
From the graph, the slope of x + y = 5 is -1 and the y-intercept is 5
The slope of x – y = 2 is 1 and the y-intercept is -2.
The point of intersection is (3.5, 1.5)
c) Use the graph in b) to solve the system of linear equations.
Answer:
Therefore the solution oi me system or equations is x = 3.5 and y = 1.5.
x = 3.5; y = 1.5
Question 3.
x + 2y = 5
2x – 2y = 1
a) Graph x + 2y = 5 and 2x — 2y = 1 on the same coordinate plane. Find the point of intersection of the graphs.
Answer:
x + 2y = 5
2x – 2y = 1
We are given the system of equations:
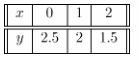
For the equation x + 2y = 5 we build the table of values:
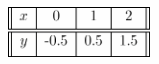
For the equation 2x — 2y = 1 we build the table of values:
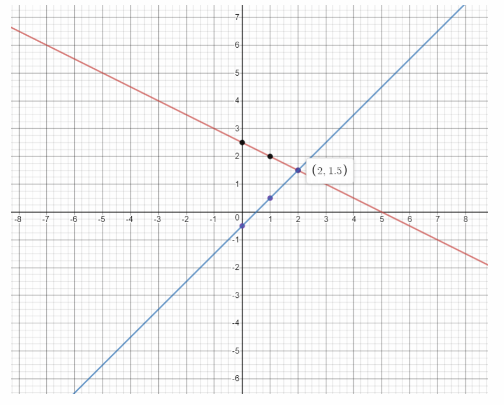
We graph the two lines:
b) Use the graph in a) to solve the system of linear equations.
Answer:
From the graph, the slope of x + 2y = 5 is -0.5 and the y-intercept is 25.
The slope of 2x – 2y = 1 is 1 and the y-intercept is -0.5.
The point of intersection is (2, 1.5). Therefore the solution of the system of equations is x = 2 and y = 1.5.
x = 2; y = 1.5
Question 4.
2x + 3y= -1
x – 2y = 3
a) Graph 2x + 3y = -1 and x – 2y = 3 on the same coordinate plane. Find the point of intersection of the graphs.
Answer:
2x + 3y = -1
x – 2y = 3
We are given the system of equations:
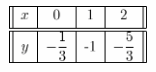
For the equation 2x + 3y = -1 we build the table of values:
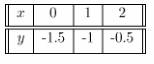
For the equation x — 2y = 3 we build the table of values:
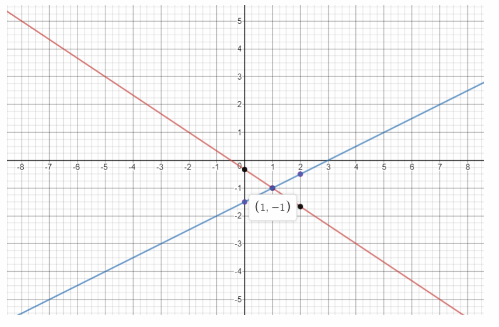
We graph the two lines:
b) Use the graph in a) to solve the system of linear equations.
Answer:
From the graph, the slope of 2x + y = 5 is –\(\frac{2}{3}\) and the y-intercept is –\(\frac{1}{3}\)
The slope of x – 2y = 3 is 0.5 and the y-intercept is -1.5.
The point of intersection is (1, -1). Therefore the solution of the system of equations is x = 1 and y = -1.
x = 1: y = -1
Solve each system of equations using the graphical method.
Question 5.
x = 2y
y = x + 2
Answer:
x = 2y Equation 1
y = x + 2 Equation 2
We are given the system of equations:
y = 0.5x We rewrite Equation 1 in slope-intercept form:
y = x + 2 Equation 2 is written in slope-intercept form:
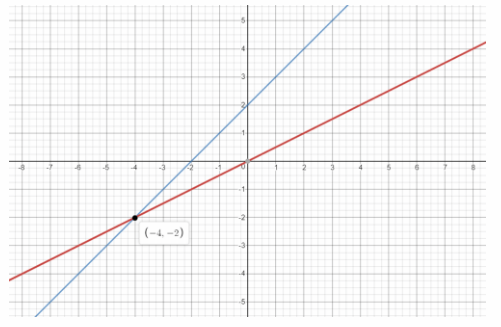
We graph the two equations: the first has slope 0.5 and y-intercept 0, while the second has slope 1 and y-intercept 2:
The point of intersection is (-4, -2). Therefore the soLution of the system of equations is x = -4 and y = -2.
Question 6.
y = 3
y = 2x + 1
Answer:
y = 3 Equation 1
y = 2x + 1 Equation 2
We are given the system of equations:
y = 3 Equation 1 is written in slope-intercept form:
y = 2x + 1 Equation 2 is written in slope-intercept form:
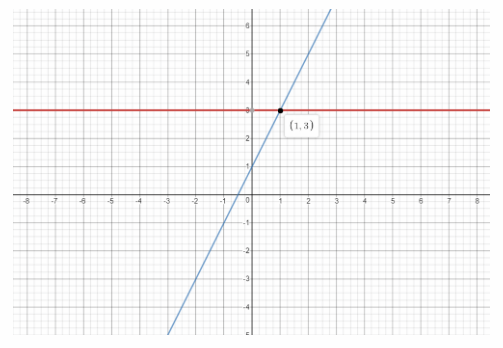
We graph the two equations: the first has slope 0 and y-intercept 3 (horizontal line), while the second has slope 2 and y-intercept 1:
The point of intersection is (1, 3). Therefore the solution of the system of equations is x = 1 and y = 3.
x = 1; y = 3
Question 7.
x = 2
y = 2x – 8
Answer:
x = 2 Equation 1
y = 2x — 8 Equation 2
We are given the system of equations:
x = 2 Equation 1 is the equation of a vertical line:
y = 2x – 8 Equation 2 is written in slope-intercept form:
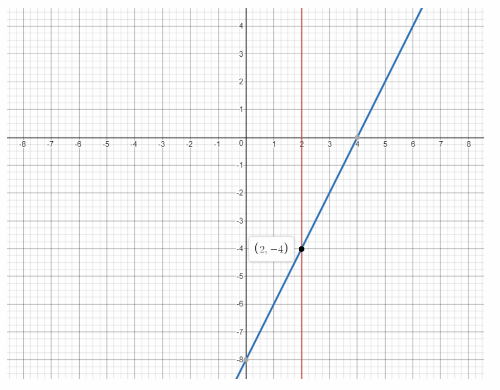
We graph the two equations: the first is vertical passing through (2, 0), while the second slope 2 and y-intercept-8:
The point of intersection is (2, -4). Therefore the solution of the system of equations is x = 2 and y = -4.
x = 2 ; y = -4
Question 8.
3x – 2y = 19
3y = 2x – 21
Answer:
3x – 2y = 19 Equation 1
3y = 2x — 21 Equation 2
We are given the system of equations:
3x – 2y – 3x = 19 – 3x We rewrite Equation 1 in slope-intercept form:
-2y = -3x + 19
y = \(\frac{3}{2}\)x – \(\frac{19}{2}\)
y = \(\frac{3}{2}\)x – \(\frac{19}{2}\)
y = \(\frac{2}{3}\)x – 7
We rewrite Equation 2 in slope-intercept form:
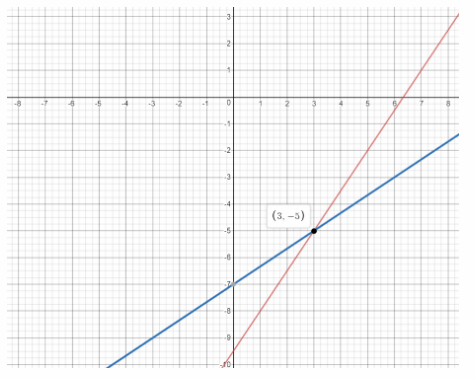
We graph the two equations: the first has slope \(\frac{3}{2}\) and y-intercept –\(\frac{19}{2}\), while the second has slope \(\frac{1}{2}\) and y-intercept -7:
The point of intersection is (3, -5) Therefore the solution of the system of equations is x = 3 and y = -5.
x = 3; y = -5
Question 9.
2x + y = 11
x + 3y = 18
Answer:
2x + y = 11 Equation 1
x + 3y = 18 Equation 2
We are given the system of equations:
2x + y — 2x = 11 – 2x We rewrite Equation 1 in slope-intercept form:
y = 11 — 2x
x + 3y — x = 18 – x We rewrite Equation 2 in slope-intercept form:
3y = 18 – x
y = –\(\frac{1}{3}\)x + 6
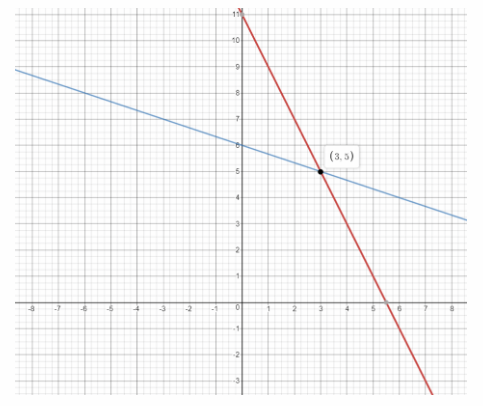
We graph the two equations: the first has slope -2 and y-intercept 11, while the second has slope –\(\frac{1}{3}\) and y-intercept 6:
The point of intersection is (3, 5). Therefore the solution of the system of equations is x = 3 and y = 5
x = 3, y = 5
Question 10.
x + 2y = 1
4y – x = 17
Answer:
x + 2y = 1 Equation 1
4y — x = 17 Equation 2
We are given the system of equations:
x + 2y – x = 1 – x We rewrite Equation 1 in slope-intercept form:
2y = -x + 1
y = –\(\frac{1}{2}\)x + \(\frac{1}{2}\)
4y — x + x = 17 + x We rewrite Equation 2 in slope-intercept form:
4y = x + 17
y = \(\frac{1}{4}\)x + \(\frac{17}{4}\)
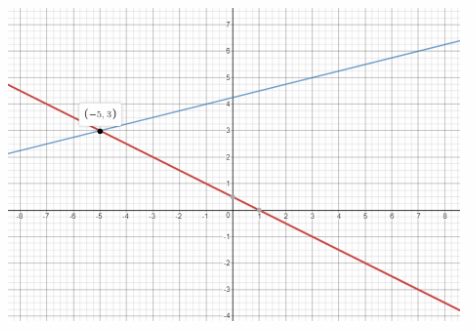
We graph the two equations: the first has slope –\(\frac{1}{2}\) and y-intercept \(\frac{1}{2}\), while the second has slope \(\frac{1}{4}\) and y-intercept \(\frac{17}{4}\)
The point of intersection is (-5, 3) Therefore the solution of the system of equations is x = -5 and y = 3.
x = -5; y = -3
Solve. Show your work.
Question 11.
Marianne jogged from point P to point Q while Walter jogged from point Q to point P. Point P and point Q are 7.5 kilometers apart. Marianne’s motion is represented by d = 8t and Walter’s motion is represented by 2d + 14t = 15, where t hours is the time and d kilometers is the distance from point P.
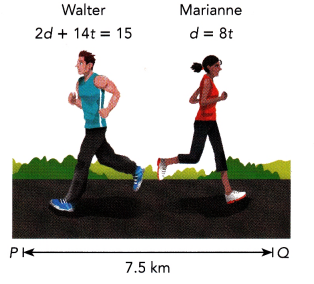
a) Solve the system of linear equations using the graphical method.
Answer:
We are given the system of equations:
d = 8t Equation 1
2d + 14t = 15 Equation 2
d = 8t a) Equation 1 is written in slope-intercept form:
2d + 14t — 14t = 15 — 14t We rewrite Equation 2 in slope-intercept form:
2d = -14t + 15
d = -7t + 7.5
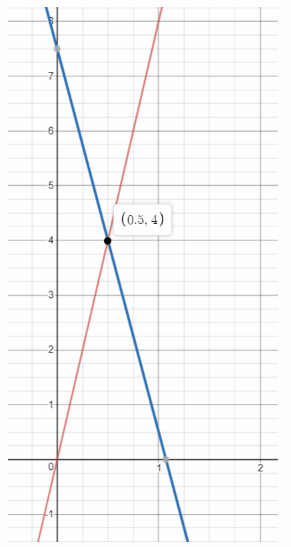
img 36
We graph the two equations the first has slope 8 and y-intercept 0, while the second has sope -7 and y-
intercept 7.5:
The point of intersection is (0.5, 4). Therefore the solution of the system of equations is t = 0.5 and
d = 4.
b) When did Marianne and Walter meet? How far from point Q did they meet?
Answer:
t = 0.5 hours b) The t-coordinate of the intersection point s the time after which they met
d = 4 km The d-coordinate of the intersection point is the distance from point P when they met:
7.5 — 4 = 3.5 km The distance from point Q is
a) t = 0.5; d = 4
b) 0.5 hours; 3.5 km
Question 12.
Math Journal Explain when it is convenient to use each method of solving a system of linear equations: Elimination, substitution, and graphical. Give an example for each method.
Answer:
3x – 4y = 25
2x + 5y = 77
The elimination method is used when none of the variables has coefficient 1.
For example:
y = 2x + 3
3x – 2y = 7 The substitution method ¡s used when one of the variables has coefficient 1
For example:
y = 2x + 1
y = -x + 2
The graphical method is used when one of the variables has coefficient 1 in both equations.
For example:
The choice depends on the coefficients of the variables
Question 13.
Two cyclists are traveling along a track in the same direction. Their motions are described by the linear equations d = 10t and d – 8t = 2, where t hours is the time and d miles is the distance from point A on the-Track.
Answer:
d = 10t Equation 1
d – 8t = 2 Equation 2
We are given the system of equations:
a) Solve the system of linear equations using a graphing calculator.
Answer:
d = 8t a) Equation 1 is written in sLope-intercept form:
d — 8t + 8t = 2 + 8t We rewrite Equation 2 in slope-intercept form:
d = 8t + 2
We graph the two equations using a graphing calculator:
3d?
The point of intersection is (1,10). Therefore the solution of the system of equations is t = 1 and d = 10.
b) When will the cyclists meet?
Answer:
t = 1 hour b) The t-coordinate of the intersection point is the time after which they met
a) t = 1; d = 10
b) 1 hour
Question 14.
Dr. Murray is heating a beaker containing Liquid A and a beaker containing Liquid B. The temperature of Liquid A is represented by T = 2t + 140 and the temperature of Liquid B is represented by T = t + 160, where T°F is the temperature of the liquid after t seconds.
Answer:
T = 2t + 140 Equation 1
T = t + 160 Equation 2
We are given the system of equations:
a) Solve the system of linear equations using a graphing calculator.
Answer:
Equation 1 and Equation 2 are written in slope-intercept
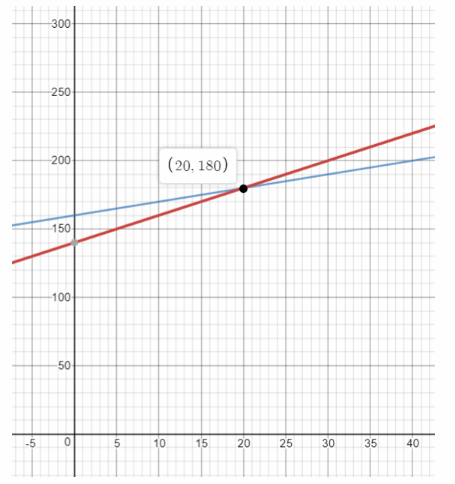
We graph the two equations using a graphing calculator:
The point of intersection is (20, 180). Therefore the solution of the system of equations is t = 20 and T = 180.
b) When will the temperatures of the liquids be the same?
Answer:
t = 20 seconds b) The t-coordinate of the intersection point is the time after which the temperatures are
the same:
a) t = 20;T = 180;
b) 20 seconds
Question 15.
A carpenter is hammering an iron nail and another carpenter is hammering a copper nail. The temperatures of the nails increase during the hammering. The temperature of the iron nail is represented by T = 2t + 70 and the temperature of the copper nail is represented by T = 3t + 65, where T°F is the temperature of the nail after t seconds.
Answer:
T = 2t + 70 Equation 1
T = 3t + 65 Equation 2
We are given the system of equations:
a) Solve the system of linear equations using a graphing calculator.
Answer:
Equation 1 and Equation 2 are written in slope-intercept form.
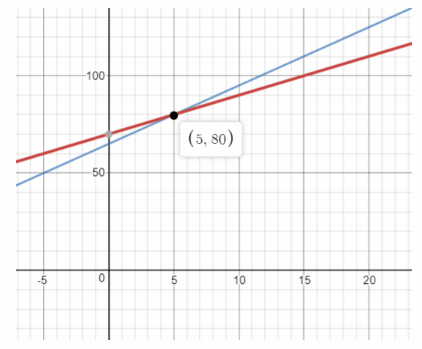
We graph the two equations using a graphing calculator
The point of intersection is (5, 80). Therefore the solution of the system of equations is t = 5 and T = 80.
b) When will the temperatures of the nails be the same?
Answer:
t = 5 seconds b) The t-coordinate of the intersection point is the time after which the temperatures are
the same:
a) t = 5; T = 80;
b) 5 seconds