Math in Focus Grade 8 Chapter 5 Lesson 5.3 Answer Key Real-World Problems: Systems of Linear Equations

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 5 Lesson 5.3 Real-World Problems: Systems of Linear Equations to score better marks in the exam.

Math in Focus Grade 7 Course 3 A Chapter 5 Lesson 5.3 Answer Key Real-World Problems: Systems of Linear Equations

Math in Focus Grade 8 Chapter 5 Lesson 5.3 Guided Practice Answer Key

Solve using systems of linear equations.

Question 1.
Two bowls and one cup have a mass of 800 grams. One bowl and two cups have a mass of 700 grams. Find the mass of a bowl and the mass of a cup.
Let the mass of a bowl be b grams and the mass of a cup be c grams.
Mass of two bowls and on cup:  =  – Equation 1

Mass of one bowl and two cups:  =  – Equation 2

Use Equation 1 to express c in terms of b:

The mass of a bowl grams and the mass of a cup is grams.
Answer:
The mass of a bowl is 300 grams and
the mass of a cup is 200 grams,

Explanation:

Solve using systems of linear equations.

Question 2.
Elizabeth is thinking of a two-digit number. When the tens digit is subtracted
from the ones digit, the difference is 2. One-fifth of the number is 1 less than
the sum of the digits. What is the number?
Answer:
Let the tens digit be c and the ones digit be d.
Tens digit subtracted from ones digit:

If the tens digit is c and the ones digit is d, then the value of the number is 10c + d.

Substitute 3 for c into Equation 3:
d = 5
=
The number is .
Answer:

Question 3.
Christopher is thinking of two positive integers.
The sum of the integers is 27. When twice the first integer is added to
half of the second integer, the sums 24. Find i the integers.

Answer:
The integers are x =7 and y = 20,

Explanation:
Given Christopher is thinking of two positive integers.
Let numbers be x and y , x+y = 27,
When twice the first integer is added to
half of the second integer, the sums 24,
2x +y/2 = 24,
x = 27-y,
2(27-y) + y/2 = 24,
4(27-y)+y = 48,
108-4y +y = 48,
108-3y = 48,
3y = 108-48,
3y = 60,
y = 60/3 = 20 and x = 27-20 = 7.

Math in Focus Course 3A Practice 5.3 Answer Key

Solve using systems of linear equations.

Question 1.
Jean stocked her aquarium with 36 fresh-water fish, which cost $212.
The male fish cost $5 each, while the female fish cost $7 each.
Find the number of male fish and the number of female fish.

Answer:
The number of male fish is 20 and the number of female fish is 16,

Explanation:
Given Jean stocked her aquarium with 36 fresh-water fish, which cost $212.
The male fish cost $5 each, while the female fish cost $7 each.
Lets take male fish as M and female fish as F,
M + F = 36, M = 36-F and 5M +7F = 212,
5(36-F) +7F = 212,
180- 5F +7F = 212,
2F = 212-180= 32,
F = 32/2 = 16, So M = 36 – 16 = 20.
The number of male fish is 20 and the number of female fish is 16.

Question 2.
Seventy concert tickets were sold for $550. Each adult ticket cost
$9 and each children’s ticket cost $5.
Find the number of adult tickets and the number of children’s tickets sold.
Answer:
50 is the number of adult tickets and 20 is the number of children’s tickets sold,

Explanation:
Given Seventy concert tickets were sold for $550. Each adult ticket cost
$9 and each children’s ticket cost $5. Let number of adult tickets be a and
number of children tickets is c, a + c = 70, a = 70 -c, 9a +5c = 550,
9(70-c) + 5c = 550,
630 – 9c +5c = 550,
630-550 = 4c,
80 = 4c,
c = 80/4 = 20,
so a= 70 – 20 = 50 tickets.
50 is the number of adult tickets and 20 is the number of children’s tickets sold.

Question 3.
George paid $2.75 for 4 granola bars and 1 apple.
Addison paid $2.25for 2 granola bars and 3 apples.
Find the cost of each granola bar and each apple.
Answer:
The cost of each granola is $0.6 and each apple is $0.35,

Explanation:
Given George paid $2.75 for 4 granola bars and 1 apple.
Addison paid $2.25 for 2 granola bars and 3 apples.
Lets take granola as g and apple as a
4g+ a = 2.75, a = 2.75 -4g
2g +3a = 2.25, substituting
2g +3 (2.75 -4g)= 2.25,
2g +8.25 – 12g = 2.25,
10g = 8.25-2.25,
10g = 6,
g = 6/10= $0.6,
a = 2.75 – 4 X 0.6 = 2.75 – 2.4 = $0.35,
The cost of each granola is $0.6 and each apple is $0.35.

Question 4.
4 thumb drives and 1 compact disk have a total capacity of 9 gigabytes.
5 thumb drives have 9 gigabytes more capacity than 1 compact disk.
Find the capacity of 1 thumb drive and the capacity of 1 compact disk.
Answer:
The capacity of 1 thumb drive is 2GB and
the capacity of 1 compact disk is 1 GB,

Question 5.
A book cover has the length and width (in inches) shown in the diagram.

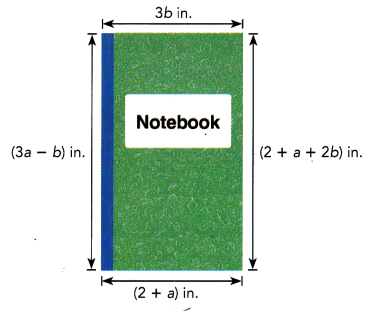
a) Find the values of a and b.
Answer:
a=4in and b = 2in,

Explanation:
We have equations  (3a-b) = 2+a+2b,
3a – a = 2+2b +b,
2a = 2 + 3b,
2a – 3b = 2  equation 1
and 3b = 2+a means  2a -2-a =2,
a =4 so 3b = 2+4 = 6, b= 6/3 = 2. ,
therefore a = 4in and b = 2in.

b) Find the perimeter of the book cover.
Answer:
Peimeter of the book cover is 32in,

Explanation:
Given l = 3a-b = 3 x 4 – 2 = 12-2 = 10, width = 3 b = 3 X 2 = 6,
perimeter = 2(l+w) = 2(10+ 6)= 2(16)= 32 in.

Question 6.
Eileen saves dimes and quarters. She has 40 coins,
which totaled $6.55, in her bank. How many of each coin does she have?
Answer:
Eileen has 23 dimes and 17 quarters,

Aiden is a percussionist in his school band. One instrument he
plays is in the shape of an equilateral triangle shown below.
The side lengths are in inches. Find x and y.

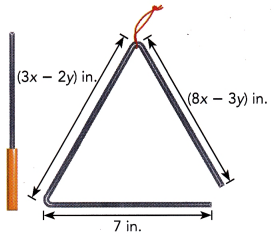
Answer:
x = -1 and y = -5,
Explanation:
Given Aiden is a percussionist in his school band. One instrument he
plays is in the shape of an equilateral triangle so
3x – 2y = 7,
3x = 2y +7,
x = (2y +7)/3,
8x – 3y = 7 substituting x
8(2y +7)/3 = 7+3y,
16y +56 = 3(7 +3y)
16y +56 = 21 +9y
16y -9y = 21-56,
7y = -35, y = -35/7 = -5,x=(2X -5+7)/3 = (-10+7)/3 = -3/3 = -1.

Question 8.
Mrs. Green gave three riddles for her class to solve.

a) The sum of the digits of a two-digit number is 11.
Twice the tens digit plus 2 equals ten times the ones digit. What is the number?
Answer:
The number is 92,

Explanation:
Given the sum of the digits of a two-digit number is 11.
x + y = 11,y = 11-x
Twice the tens digit plus 2 equals ten times the ones digit
2x + 2 = 10y,
2x + 2 = 10(11-x),
2x +2 = 110 -10x,
2x +10x = 110-2,
12x = 108, x = 108/12 = 9, so y = 11-9 = 2,
the number is 92.

b) There are two numbers. The first number minus the second number is 15.
One-third of the sum of the numbers is one quarter of the first number.
What are the two numbers?
Answer:
The two numbers are 12 and -3,

Explanation:
Let x and y be the numbers ,
The first number minus the second number is 15. x – y = 15,
(x +y)/3 = x/4,
4x + 4y = 3x,
x = -4y, substituting  -4y – y = 15,
-5y = 15, y = -15/5 = -3,
x = – 4(-3) = 12.
The two numbers are 12 and -3.

c) A two-digit number is 1 more than eight times the sum of the digits.
The ones digit is 3 less than the tens digit. What is the number?
Answer:
The number is 41,

Explanation:
Given A two-digit number is 1 more than eight times the sum of the digits.
10x + y = 8(x+y)+1
The ones digit is 3 less than the tens digit means x = y +3,
10(y +3)+y = 8(y+3) +8y +1,
10 y + 30 +y = 8y + 24 +8y +1,
11y + 30 = 16 y +25,
16y – 11y = 30 -25,
5y = 5, y = 5/5 = 1, x = 1+ 3 = 4,
The number is 41.

Question 9.

On Saturday, $585 was collected from the sale of 55 tickets for a performance.
The table below shows the information about the sale of the tickets.
Find the number of adult tickets and the number of student’s tickets sold on that day.

Answer:
30 number of adult tickets and 25 number of student’s tickets sold on that day,

Explanation:
Given Students tickets cost 12 X .25 = 3, 12-3 =9 is the cost for student tickets,
Let a be the number of adult tickets and s the number of
student’s tickets sold on that day, a + s = 55 , s = 55-a and
12a +9s = 585,
12a+9(55 -a) = 585,
12a + 495 -9a = 585,
3a = 585- 495= 90,
a= 90/3 = 30, s = 55-30 = 25.
30 number of adult tickets and 25 number of student’s tickets sold on that day.

Question 10.
Eight years ago, Mr. Fontana was six times as old as his son.
In twelve years’ time, he will be twice as old as his son. How old are they now?

Answer:
Fathers age is 38 and sons age is 13 years old,
Explanation:
Let f be fathers age now and s be sons age now,
Eight years ago, Mr. Fontana was six times as old as his son.
f – 8 = 6(s -8), In twelve years’ time, he will be twice as old as his son,
f + 12 = 2(s+12),
f = 2s +24-12 = 2s+12,
2s +12 – 8 = 6s – 48,
2s +4 = 6s -48,
6s-2s = 48+4,
4s = 52,
s = 52/4 = 13, f = 2 X 13 +12 = 26 +12 = 38.
Fathers age is 38 and sons age is 13 years old.

Question 11.
A restaurant sells four combo meals. Jolly Meal, which cost $12.60,
consists of 2 yogurt cups and 1 sandwich. The $pecial Meal, which is
made up of 2 sandwiches and 1 yogurt cup, cost $13.50.
Calculate the cost of the following combo meals if the charge for
sandwiches and yogurt cups are the same for all combo meals.
a) Children’s Meal: 1 sandwich and 1 yogurt cup
Answer:
Children’s Meal: 1 sandwich and 1 yogurt cup is $8.7,

Explanation:
Given a restaurant sells four combo meals.
Jolly Meal, which cost $12.60, consists of 2 yogurt cups and 1 sandwich.
The $pecial Meal, which is made up of 2 sandwiches and 1 yogurt cup, cost $13.50.
Let sandwiches is s and yogurt is y
Jolly Meal 2y +s = $12.60, s = 12.60 – 2y,
2s +y = $13.50,
2 (12.60 -2y)+y =13.50,
25.2 – 4y +y = 13.50,
25.2-13.50 = 3y,
3y = 11.7,y = 11.7/3 = 3.9,
so s = 12.60 – 2(3.9) = 12.60 – 7.8 = 4.8,
therefore 1 sandwich and 1 yogurt cup is $4.8 + $3.9 = $8.7.

b) Family Meal: 2 sandwiches and 3 yogurt cups
Answer:
Family Meal: 2 sandwiches and 3 yogurt cups is $21.3,

Explanation:
We got sandwiches s = $4.8, yogurt y = $3.9,
so for 2 sandwiches and 3 yogurt cups it is
2X $4.8 and 3 X $3.9 = $9.6 + $11.7 = $21.3.

Question 12.
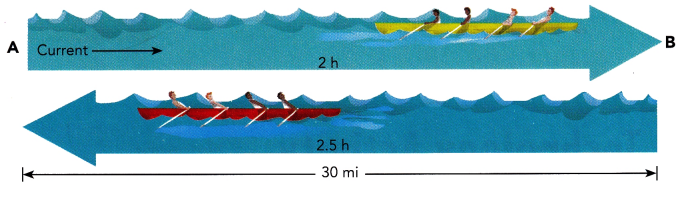
In a boat race, Jenny’s team rowed their boat from point A to point 8 and back to point A.
Points A and 8 are 30 miles apart. During the race,
there was a constant current flowing from A to 8.
She took 2 hours to travel from A to 8 and 2.5 hours to travel from 8 to A.

a) Calculate the speed of the boat from A to 6 and the speed from 8 to A.
Answer:
The effective speed of the boat downstream is 15 mph,
The effective speed of the boat upstream is 12 mph,
Explanation:
Given one way distance is 30 miles,
Down stream travel took 2 hours,
and Up stream travel took is 2.5 hours,
The effective speed downstream was 30/2 = 15 miles per hour,
The effective speed upstream was 30/2.5 = 12 miles per hour,
The effective speed downstream is u + v, where u is the speed of the
boat in the still water and v is the current speed,
The effective speed up stream is u – v,
u + v = 15, u – v = 12, v = u -12,
u + (u -12) = 15,
2u = 15+ 12 = 27, u = 27/2 = 13.5 mph,
v = 13.5 – 12 = 1.5 mph

b) Find the speed of the boat from A to B if there was no current.
Answer:
The speed of the boat in still water is 13.5 mph

c) Find the speed of the current.
Answer:
The speed of the current is 1.5 mph

Question 13.
Alex deposited $3,500 in two banks. The first bank paid 2% simple interest
per year while the second bank paid 3%. At the end of one year,
the difference in the interest amounts was $30. Find the amount Alex deposited in each bank.
Answer:
Alex deposited $2,700 in one bank and $800 in another bank,

Explanation:
Given Alex deposited $3,500 in two banks,
x + y = 3500,so y = 3500-x
The first bank paid 2% simple interest
per year while the second bank paid 3% and
At the end of one year,
the difference in the interest amounts was $30.
I = pRT interest of x is x X 0.02,
Interest of y is y X 0.03,
0.02x-0.03 y = 30 multiplying both sides by 100,
2x – 3y = 3000,substituting x
2x – 3(3500 – x) = 3000,
2x – 10,500  +3x = 3000,
5x = 10,500 + 3,000= 13,500,
x = 13,500/5 = $2700, y = 3500 – 2700 = $800,
Alex deposited $2,700 in one bank and $800 in another bank.

Question 14.
Greg’s favorite activities are bike riding and hip-hop dancing.
He wants to try to do these activities for 6 hours each week.
He would also like to try to burn off about 2,100 calories a week.
He finds that biking uses about 425 calories each hour and
hip-hop dancing uses about 325 calories each hour.
He wants to do bike riding for x hours and hip-hop dancing for y hours each week.

a) Copy and complete the following table.

Answer:

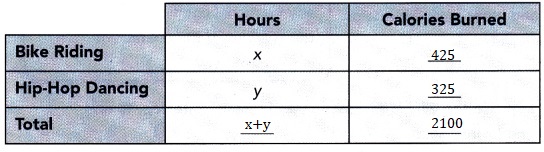
Explanation:
Copied and completed the table as shown above.

b) How much time should he spend doing each activity to accomplish his goal?
Answer:
Greg’s wants to do bike riding for 3/2 or 1.5 hours and
hip-hop dancing for 9/2 or 4.5 hours eqch week,

Explanation:
Given Greg’s favorite activities are bike riding and hip-hop dancing.
He wants to try to do these activities for 6 hours each week.
He would also like to try to burn off about 2,100 calories a week.
He finds that biking uses about 425 calories each hour and
hip-hop dancing uses about 325 calories each hour.
Let x hours is bike riding and y hours br hip hop dancing so
x + y = 6, y = 6 – x and 425x + 325y = 2,100 substituting y
425x +325(6-x) =2100,
425x + 1950 – 325x = 2100,
100x = 2100-1950=150,
x = 150/100 = 3/2, y = 6-3/2 = 9/2,
So Greg’s wants to do bike riding for 3/2 or 1.5 hours and
hip-hop dancing for 9/2 or 4.5 hours each week.

Question 15.
In an experiment, Matthew was given two saline (salt) solutions,
whose concentrations are shown below. He had to prepare 10 fluid ounces of
a new saline solution with a 27% concentration from the two solutions.
Calculate the volume of each solution used to prepare the new solution.

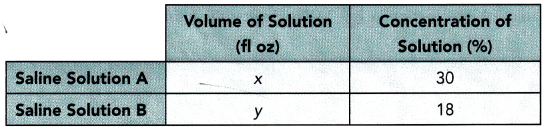
Answer:
The volume of each solution used to prepare the new solution is
x as 7.5 fl oz and y as 2.5 fl oz,

Explanation:
Given Matthew was given two saline (salt) solutions,
whose concentrations are 30 and 18. He had to prepare 10 fluid ounces of
a new saline solution with a 27% concentration from the two solutions.
The volume of each solution used to prepare the new solution is
30x +18 y = 270 and x + y = 10, y = 10 -x,
30 x+18(10-x)=270,
30x +180 – 18x = 270,
12 x = 270-180,
12x = 90, x= 90/12 = 7.5 and y= 10-7.5 = 2.5, therefore
the volume of each solution used to prepare the new solution is
x as 7.5 fl oz and y as 2.5 fl oz.