Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 5 Lesson 5.2 Solving Systems of Linear Equations Using Algebraic Methods to score better marks in the exam.
Math in Focus Grade 7 Course 3 A Chapter 5 Lesson 5.2 Answer Key Solving Systems of Linear Equations Using Algebraic Methods
Math in Focus Grade 8 Chapter 5 Lesson 5.2 Guided Practice Answer Key
Solve each system of linear equations using the elimination method.
Question 1.
2a+ 3b= 29 —Equation 1
2a — b = 17 — Equation 2
Subtract Equation 2 from Equation 1:

Answer:
The solution to the system of linear equations is a = 23/2 and b =6,
Explanation:

Question 2.
2x – y = 2
3x + y = 13
Answer:
The solution to the system of linear equations is x = 3 and y =4.
Explanation:
Given 2x -y =2 -Equation 1,
3x + y = 13- Equation 2 Adding Equation 2 and 1,
2x – y =2
3x + y =13
5x = 15,
x = 15/5 = 3, substituting x =3 in Equation 1
y = 2x -2= 2 X 3 -2 = 6-2 =4.
Question 3.
x + 6 = 1
x + y = 6
Answer:
The solution to the system of linear equations is x = -5 and y = 11,
Explanation:
Given x + 6 =1 means x = 1-6 = -5,
substituting x = -5 in Equation 2 – x + y = 6 as x = -5,
-5 + y = 6, y = 6 +5 = 11.
Therefore x = -5 and y = 11.
Solve each system of linear equations using the elimination method.
Question 4.
7m + 2n = -8
2m = 3n – 13
Answer:
The solution to the system of linear equations is m = -2 and n =3,
Explanation:
Given 7m +2n = -8 – Equation 1 and 2m = 3n – 13- Equation 2,
to make elmination we need common values we multiply
Equation 1 by 3 and Equation 2 by 2 so that n becomes common,
3 X(7m +2n )= 3 X -8 = 21m + 6n = -24 and
2 X 2m = 2 X (3n – 13)= 4m = 6n – 26 means 6n = 4m + 26,
so 21m + 4m + 26 = -24, 25m = -24-26,
25m = -50,
m = -50/25 = -2, so substituting m= -2 in 2m = 3n -13,
2(-2)+13 = 3n,
-4+13 = 3n,
3n = 9, n = 9/3 = 3.
Question 5.
3x – 2y = 24
5x + 4y = -4
Answer:
The solution to the system of linear equations is x = 4 and y = -6,
Explanation:
Given Equation 1 as 3x -2y = 24 and Equation 2 as 5x +4y = -4,
to make elmination we need common values we multiply
Equation 1 by 2 so that y can be elminated,
2X(3x-2y =24)= 6x -4y = 48 adding with Equation 2
6x -4y =48
(+)5x +4y = -4
11x = 44,
x = 44/11 = 4, we substitute x = 4 in Equation 1 ,
3 X 4 – 2y = 24,
12- 2y = 24,
12-24 = 2y,
2y = -12, y = -12/2 = -6.
Question 6.
2x + 7y = -32
4x – 5y = 12
Answer:
The solution to the system of linear equations is y = -4 and x = -2,
Explanation:
Given 2x +7y = -32 Equation 1 and 4x -5y = 12 Equation 2,
to make elmination we need common values we multiply
Equation 1 by -2 so that x can be elminated,
-2 X(2x +7y=-32) = -4x – 14y = 64 now we add eqaution 1 with
equation 2 as -4x – 14y = 64
(+) 4x- 5y =12
-19y = 76, y = -76/19 =-4, substituting y =-4
4x -5(-4)=12, 4x +20 = 12, 4x = 12-20 = -8, 4x = -8 , x =-8/4 = -2.
Solve each system of linear equations by using the substitution method.
Question 7.
2x + y = 5 — Equation 1
y = 4x – 7 — Equation 2
Substitute Equation 2 into Equation 1:

Answer:
The solution to the system of linear equations is x =2 and y =1,
Explanation:

Question 8.
4x + 3y = 23 — Equation 1
5x + y = 15 — Equation 2
Use Equation 2 to express y in terms of x:
5x + y = 15

Answer:
The solution to the system of linear equations is x =2 and y = 5,
Explanation:

Question 9.
3x – y = 8
2x + 3y = 9
Answer:
The solution to the system of linear equations is x = 3 and y = 1,
Explanation:
Given 3x – y =8 Equation 1 and 2x +3y = 9 Equation 2,
we can write Equation 1 as y = 3x -8,
substituting y in Equation 2 as
2x +3 (3x -8) = 9,
2x + 9x – 24 =9,
11x = 9+ 24 = 33, x = 33/11 = 3,so y = 3 X 3 – 8 = 9-8 = 1.
Question 10.
7m + 2n = -8
2m = 3n – 13
Answer:
The solution to the system of linear equations is m = -2 and n =3,
Explanation:
Given 7m +2n = -8 Equation 1 and 2m = 3n – 13 Equation 2,
to make elmination we need common values we multiply
Equation 1 by 3 and Equation 2 by 2 so that n can be elminated as
3(7m +2n =-8) = 21m +6n = -24 – equation 3and
2(2m = 3n -13) = 4m = 6n – 26 means 6n = 4m +26 substituting 6n in eqaution 3
21m +4m + 26 = -24,
25m = -24 -26 = -50 , m = -50/25 = -2, now
6n = 4(-2)+ 26 = -8 +26 = 18,
6n = 18, n = 18/6 = 3.
Solve each system of linear equations using elimination method or
substitution method. Explain why you choose each method.
Question 11.
2x + 3y = 29
2x – 17 = y
Answer:
The solution to the system of linear equations is x = 10 and y = 3,
used substitution method as already y is given in Equation 2,
Explanation:
Given 2x+3y = 29 as equation 1 and y already there ,
so we use substitution method as y = 2x -17 in equation 1
2x + 3(2x – 17) = 29,
2x + 6x – 51= 29,
8x = 29 +51= 80,
x = 80/8 = 10,
y = 2 X 10 -17 = 20 -17 = 3.
Question 12.
3a – 2b = 5
2a – 5b = 51
Answer:
The solution to the system of linear equations is a= -7 and b = -13,
Used elmination method because of no common values of a and b,
Explanation:
Given 3a- 2b =5 Equation 1 and 2a – 5b = 51 in Equation 2 in both
equations a or b is not common so we use elmination and we multiply
equation 1 by 2 2(3a-2b =5) = 6a – 4b = 10 and equation 2 by 3
3(2a -5b = 51) = 6a – 15b = 153 subtracting eqaution 2 from eqaution 1
6a-4b =10
(-) -6a +15b =-153
11 b = -143,
b = – 143/11 = -13, substituting in eqaution 1
3a -2(-13)=5,
3a +26 =5,
3a = 5 -26 = -21,
a = -21/3 = -7.
Math in Focus Course 3A Practice 5.2 Answer Key
Solve each system of linear equations using the elimination method.
Question 1.
2j + k = 6
j – k = 8
Answer:
The solution to the system of linear equations is j = 14/3 and k = -10/3,
Explanation:
Given 2j +k =6 equation 1,
j – k = 8 equation 2 adding 1 and 2
2j+j = 6 +8,
3j = 14,
j = 14/3,
k = j – 8 = 14/3 – 8 = 14- 24/3 = -10/3,.
Question 2.
2j + 3k = 11
2j – 5k = 3
Answer:
The solution to the system of linear equations is j =4 and k =1,
Explanation:
Given 2j +3k = 11 – Equation -1, 2j – 5k =3- Equation -2
subtracting eqaution 2 from 1
2j +3k =11
-2j +5k = -3
8k = 8, k = 8/8 = 1, substuting k =1 in equtation 2
2j – 5 = 3, 2j = 3+5 = 8, j = 8/2 = 4.
Question 3.
3m + n = 30
2m – n = 20
Answer:
The solution to the system of linear equations is m = 10, n =0.
Explanation:
Given 3m + n = 30 Equation 1, 2m -n = 20 Equation 2
adding 1 and 2 we get
3m +n =30
2m – n =20
5m = 50, m = 50/5 = 10, substituting m = 10 in equation2
2 X 10 – n =20,
n = 20 – 20 = 0.
Question 4.
3x – y = 9
2x – y = 7
Answer:
The solution to the system of linear equations is x =2 and y = -3,
Explanation:
Given 3x -y = 9 Equation 1 and 2x -y =7 Equation 2,
subtracting eqaution 2 from 1
3x -y =9
-2x +y =-7
x = 2, substituting x =2 in 2(2)-y = 7,
y = 4 – 7 = -3,
Question 5.
5s – t = 12
3s + t = 12
Answer:
The solution to the system of linear equations is s = 3 and t =3,
Explanation:
Given 5s -t =12 as equation 1 and 3s +t = 12 equation 2 adding1 & 2
5s -t =12,
(+)3s+t =12
8s = 24, s = 24/8 = 3, substituting s = 3 in eqaution 2
t = 12 – 3s,
t = 12 – 3 X 3 = 12-9 = 3.
Question 6.
2b + c = 10
2b – c = 6
Answer:
The solution to the system of linear equations is b = 4 and c = 2,
Explanation:
Given 2b + c = 10 as equation 1 and
2b – c =6 as equation 2 adding euqtion 1 & 2
2b +c =10
(+) 2b -c =6
4b = 16, b = 16/4 = 4, substituting b = 4 in equation 2
2X4 -6 = c,
c = 8-6 = 2.
Question 7.
3m – n = 7
21m + 6n = -29
Answer:
The solution to the system of linear equations is m = 1/3 and n = -6,
Explanation:
Given 3m – n = 7 as equation 1 means n = 3m -7,
21m +6n = -29 is equation 2 substituting n = 3m -7 in equation 2
21m +6(3m -7) = -29,
21m +18m – 42 = -29,
39m = -29+42,
39m = 13,
m = 13/39 = 1/3, substituting n = 3(1/3)-7 = 1-7 = -6.
Question 8.
7a + b = 10
2a + 3b = -8
Answer:
The solution to the system of linear equations is
Explanation:
Given 7a + b = 10 as equation 1 we get b = 10-7a,
we have 2a + 3b = -8 as equation 2 substituting b = 10-7a in
equation 2 –2a +3(10-7a) =-8,
2a + 30 – 21a = -8,
-19a = -8 -30
a = 38/19= 2, substituting a=2 in b = 10 -7 X2 = 10 – 14 = -4.
Question 9.
2p + 5q = 4
7p + 15q = 9
Answer:
The solution to the system of linear equations is p= -3 and q = 2,
Explanation:
Given 2p +5q = 4 as eqaution 1 and 7p +15 q = 9 as equation 2,
if we multiply eqauation 1 with 3 we get 15 q so that we can easily
subtract from equation 2 so
3 X (2p +5q = 4)= equation 1 becomes
6p + 15q = 12 now we subtract equation 2
(-) 7p -15q = -9
-p = 3, p = -3 substituting p =-3 in 2p+5q = 4,
2(-3)+5q = 4,
5q = 4+6 = 10, q = 10/5 = 2.
Solve each system of linear equations using the substitution method.
Question 10.
2j + k = 3
k = j – 9
Answer:
The solution to the system of linear equations is j = 4 and k = -5,
Explanation:
Given 2j +k = 3 as equation 1 and wehave k = j -9 substituting in
equation 1 2j+(j -9) = 3,
3j = 3 + 9 = 12,
j = 12/3 = 4, therefore k = 4 – 9 = -5.
Question 11.
2h + 3k = 13
h = 2k – 4
Answer:
The solution to the system of linear equations is h =2 and k = 3,
Explanation:
Given 2h +3k = 13 as equation 1 and h = 2k-4
substituting h in equation 1 as
2 (2k-4) +3k = 13,
4k – 8 +3k = 13,
7k = 13+8= 21,
k = 21/7 = 3,So h = 2 X 3 – 4 = 6-4 =2.
Question 12.
3m + b = 23
m – b = 5
Answer:
The solution to the system of linear equations is b = 2 and m =7,
Explanation:
Given 3m+ b = 23 as equation 1 and as m-b = 5 ,
b = m-5 substituting in equation 1 3m + m -5 = 23,
4m = 23+5, 4m = 28, m= 28/4 = 7,
b = 7 – 5= 2.
Question 13.
3h – k = 10
h – k = 2
Answer:
The solution to the system of linear equations is h =4 and k =2,
Explanation:
Given 3h – k =10 as equation 1 and h -k = 2 ,
k = h -2 substituting in eqaution 1 k,
3h -h +2 = 10,
2h = 10-2 = 8,
h = 8/2 = 4 therefore k = h -2 = 4-2 =2.
Question 14.
3s – t = 5
s + 2t = 4
Answer:
The solution to the system of linear equations is s =2 and t = 1,
Explanation:
Given 3s – t = 5 as equation 1 and s +2t = 4 means
s = 4-2t substituting s in equation 1 we get
3(4-2t)- t =5,
12 – 6t – t =5,
12 -7t =5,
7t = 12-5 = 7,
t =7/7 = 1, therefore s = 4 – 2X 1 = 4-2 =2.
Question 15.
2x + y = 20
3x + 4y = 40
Answer:
The solution to the system of linear equations is x = 8 and y = 4,
Explanation:
Given 2x +y = 20 as equation 1 and 3x +4y = 40 equation2,
Equation 1 can be written as y = 20-2x and
sustituted in equation 2 as 3x +4 (20-2x) = 40,
3x + 80 – 8x = 40,
-5x = 40 -80= -40,
5x = 40,
x = 40/5 = 8, so y = 20 -2 X 8 = 20 -16 =4.
Question 16.
3x + 2y = 0
5x – 2y = 32
Answer:
The solution to the system of linear equations is x = 4 and y = -6,
Explanation:
Given 3x+ 2y = 0 as equation 1 and 5x -2y = 32 as equation 2,
adding equation 1 and 2 we get
3x +2y =0,
5x -2y = 32
8x = 32,
x = 32/8 = 4 substituting x = 4 in equation 1
3(4) +2y = 0,
2y = -12, y = -12/2 = -6.
Question 17.
5x – y = 20
4x + 3y = 16
Answer:
The solution to the system of linear equations is x = 4 and y =0,
Explanation:
Given 5x – y = 20 as equation 1 and 4x +3y = 16 as equation 2
From equation 1 we have y = 5x -20,
substituting y in equation 2
4x + 3(5x -20) = 16,
4x + 15x – 60 = 16,
19x = 16 +60,
19 x = 76,
x = 76/19 = 4, so y = 5 x 4 – 20 = 0.
Question 18.
3p + 4q = 3
\(\frac{1}{2}\) + q = 3p
Answer:
The solution to the system of linear equations is p =\(\frac{1}{3}\) and
q = \(\frac{1}{2}\),
Explanation:
Given 3p +4q = 3 as equation 1 and \(\frac{1}{2}\) + q = 3p as equation 2
q = 3p – (1/2) substituting in equation 1
3p+4(3p – 1/2) =3,
3p +12 p – 2 = 3,
15p = 3+2 = 5,
p = 5/15 = 1/3, now q = 3 X 1/3 -1/2 = 1 – 1/2 = 1/2,
so p =\(\frac{1}{3}\) and q = \(\frac{1}{2}\).
Solve each system of linear equations using the elimination method or
substitution method. Explain why you choose each method.
Question 19.
2x + 7y = 32
4x – 5y = -12
Answer:
The solution to the system of linear equations is x= 2 and y =4,
used elimination method to elminate x,
Explanation:
Given 2x +7y = 32 as equation 1 and we have
4x – 5y = -12 as equation 2 if we multiply equation 1 by 2 and
subtarct equation 2 we can eliminate x
2X(2x +7y) = 64,
4x +14 y = 64
-4x +5y = 12
19y = 76, y = 76/19 = 4, now 4x -5 X 4= -12,
4x – 20 = -12,
4x = 8, x = 8/4 = 2.
Question 20.
3x + 3y = 22
3x – 2y = 7
Answer:
The solution to the system of linear equations is x = 13/3 and
y =3 used elmination method to elminate x,
Explanation:
Given 3x +3y = 22 as equation 1 and 3x – 2y = 7 as
equation 2 subtracting equation 2 from 1 we can eliminate x
3x + 3y = 22,
-3x +2y = -7
5y = 15, y = 15/5 = 3, substituting y =3 in eqaution 2
3x – 2 X 3 = 7,
3x = 7+6 = 13,
x = 13/3.
Question 21.
7m + 2n = 20
2m = 3n – 5
Answer:
The solution to the system of linear equations is m = 2 and n =3,
used subtitution method,
Explanation:
Given 7m + 2n = 20 as equation 1 and 2m = 3n -5,
so using substitution m = (3n-5)/2 in equation 1,
7 (3n- 5)/2 + 2n = 20
7 (3n -5) + 4n = 40,
21n – 35 + 4n = 40,
25n = 40 +35 = 75,
25n = 75, n = 75/25 = 3,
n = 3, so m = (3 X3 -5)/2 = (9-5)/2 = 4/2 = 2.
Question 22.
3h – 4k = 35
k = 2h – 20
Answer:
The solution to the system of linear equations is h = 15 and
k =10 used substitution method,
Explanation:
Given 3h – 4k = 35 as equation 1 and k =2h – 20,
substituting k in equation 1
3h – 4(2h – 20) = 35,
3h – 6h + 80 = 35,
– 3h + 80 = 35,
3h = 80-35 = 45,
3h = 45, h = 45/3 = 15, so k = 2 X 15 – 20 = 30-20 = 10.
Question 23.
2h + 7k = 32
3h – 2k = -2
Answer:
The solution to the system of linear equations is h = 2 and k = 4,
used elmination method,
Explanation:
Given 2h +7k = 32 as equation 1 and 3h – 2k = -2 as equation 2
multiplying equation 1 by 3 and eqaution 2 by 2 to elminate h,
3(2h+ 7k= 32) becomes 6h + 21 k = 96 and
2(3h – 2k=-2) becomes 6h – 4k = -4 substracting 2 from 1,
6h +21k = 96
-6h +4k = 4
25 k = 100,
k = 100/25 = 4, substituting k =4 in eqaution 2
3h – 2 X 4= -2,
3h = -2 + 8 = 6,
h = 6/3 = 2.
Question 24.
2m+4=3n
5m – 3n = -1
Answer:
The solution to the system of linear equations m = -11 and n -6,
used substitution method,
Explanation:
Given 2m+ 4 = 3n as equation 1 and 5m – 3n = -1 as equation 2,
substituting 3n in equation 2 as
5m -3(2m +4) =-1,
5m – 6m -12 = -1,
-m = -1 + 12 = 11, m = -11, therefore 3n = 2 (-11) + 4,
3n = -22 + 4 = -18,
n = -18/3 = -6.
Solve.
Question 25.
Math Journal Sam solves the following system of linear equations by the elimination method,
without using calculator.
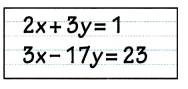
He can multiply the first equation by 3 and the second equation by 2 in order to eliminate x.
Or he can eliminate y by multiplying the first equation by 17 and the second equation by 3.
Which way should Sam choose? Explain.
Answer:
Sam can either choose any of the methods by
using method 1 he can elminate x or
by using method 2 he can elminate y and find solutions,
Explanation:
Given in method 1 sam can multiply the first equation by 3 and the
second equation by 2 in order to eliminate x and in method 2
he can eliminate y by multiplying the first equation by 17 and
the second equation by 3 therefore Sam can either choose any of the method by
using method 1 he can elminate x or
by using method 2 he can elminate y and find solutions,
Method 1 :
3 X (2x + 3y = 1) and 2 X (3x – 17 y =23)
6x + 9y =3 and
(-)6x – 34y = 46
43 y = -43, y = -43/43, y = -1, substuting y = -1 in 2x +3y = 1,
2x + 3X -1 = 1,
2x – 3 = 1,
2x = 1+3 = 4, x = 4/2 = 2.
Method 2:
17 X (2X +3y = 1) and 3 ( 3x – 17y =23),
34x + 51 y = 17
9x – 51 y = 69
43x = 86, x = 86/43 = 2, x = 2 substituting 2 X 2 + 3y = 1,
4 +3y = 1, 3y = 1-4 = -3, 3y = -3, y = -3/3 = -1,
therefore by both methods we got x =2 and y = -1 ,
Sam can either choose any of the methods.