Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 5 Lesson 5.1 Introduction to Systems of Linear Equations to score better marks in the exam.
Math in Focus Grade 7 Course 3 A Chapter 5 Lesson 5.1 Answer Key Introduction to Systems of Linear Equations
Math in Focus Grade 8 Chapter 5 Lesson 5.1 Guided Practice Answer Key
Solve the system of linear equations by copying and completing the tables of values.
The values x and y are positive integers.
Question 1.
A bottle of water and a taco cost $3. The cost of 3 bottles of water is $1 more than the cost of a taco.
Let x be the price of a bottle of water and y be the price of a taco in dollars.
The related system of equations and tables of values are:
3x – y = 1
x + y = 3
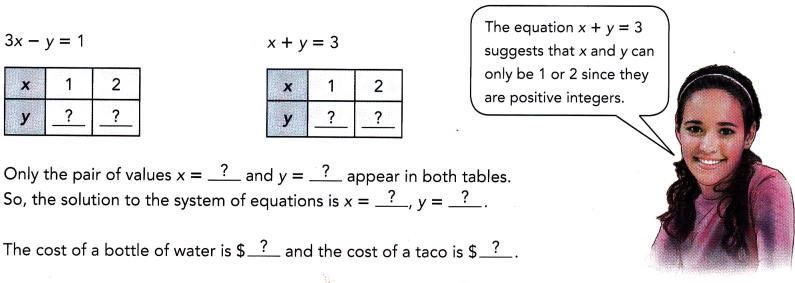
Answer:
The cost of a bottle of water is $2 and the cost of a taco is $1,
Explanation:

Solve each system of equations by making tables of values, x and y are positive integers.
Question 2.
x + y = 6
x + 2y = 8
Answer:
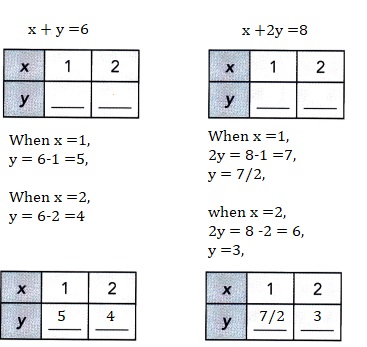
Explanation:
Solved each system of equations by making tables of values, x and y are positive integers.
For equation x+y = 6, when x =1 then y =5 and when x =2 then y=4,
For equation x +2y =8, when x =1 then y =7/2 and when x = 2 then x =3.
Question 3.
x + y = 8
x – 3y = -8
Answer:
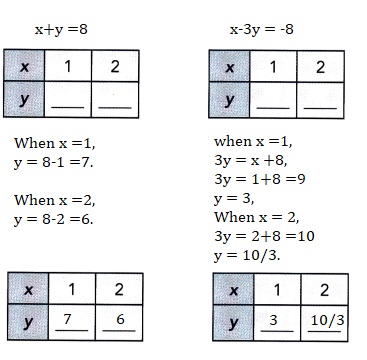
Explanation:
Solved each system of equations by making tables of values, x and y are positive integers.
For equation x+y = 6, when x =1 then y =5 and when x =2 then y=4,
For equation x +2y =8, when x =1 then y =7/2 and when x = 2 then x =3.
For each linear equation, list in a table enough values for x and y to obtain a solution.
Remember that they must be positive integers.

Technology Activity
Materials:
- graphing calculator
Use Tables On A Graphing Calculator To Solve A System Of Equations
Work in pairs.
You can use a graphing calculator to create tables of values and solve systems of equations.
Use the steps below to solve this system:
8x + y = 38
x – 4y = 13
Step 1.
Solve each equation for y in terms of x. Input the two resulting expressions for y into the equation screen.
Caution
Use parentheses around fractional coefficients and the ![]() key for negative coefficients
key for negative coefficients
Step 2.
Set the table function to use values of x starting at 0, with increments of 1.
Step 3.
Display the table. It will be in three columns as shown.
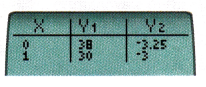
Step 4.
Find the row where the two y-values are the same. This y-value and the corresponding x-value will be the solutión to the equations.
The solution to the system of equations is given by x = ![]() and y =
and y = ![]() .
.
Math Journal How can you tell from the two columns of y-values that there is only one row where the y-values are the same?
Math in Focus Course 3A Practice 5.1 Answer Key
Solve each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.
Question 1.
2x + y = 5
x – y = -2
Answer:
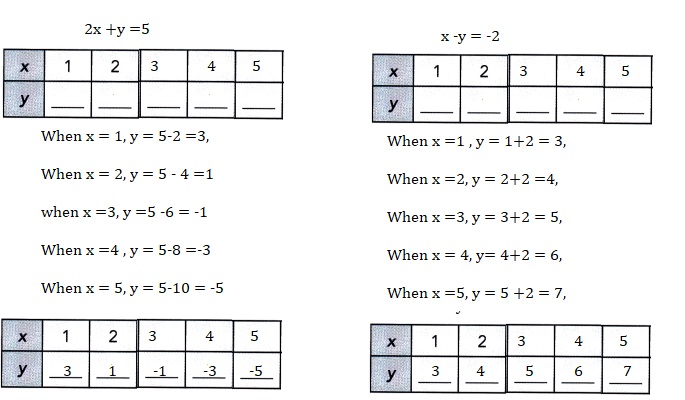
Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.
Question 2.
x + 2y = 4
x = 2y
Answer:
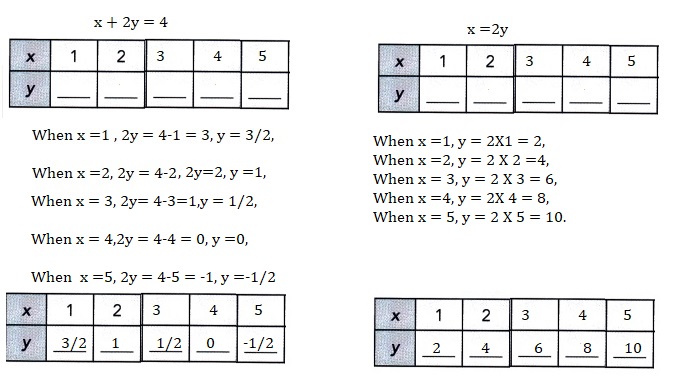
Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.
Question 3.
3x + 2y = 10
5x – 2y = 6
Answer:

Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.
Question 4.
x – 2y = -5
x = y
Answer:
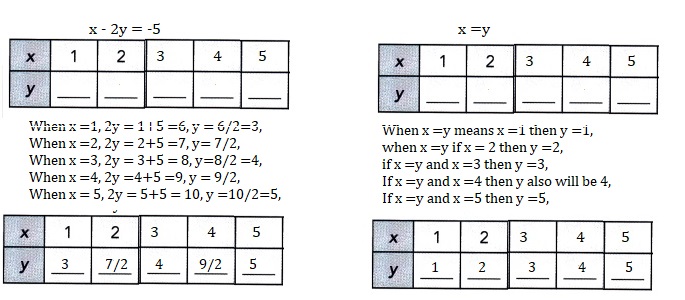
Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.
Question 5.
2y – x = -2
x + y = 2
Answer:
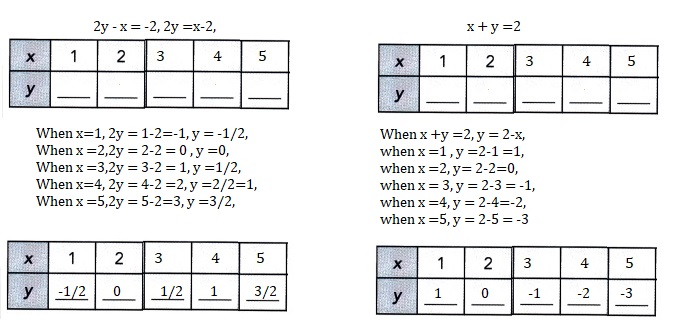
Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.
Question 6.
2x + y = 3
x + y = 1
Answer:
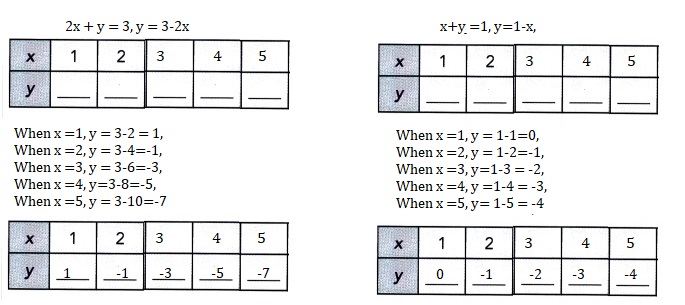
Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.
Question 7.
x + 2y = 1
x – 2y = 5
Answer:

Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.
Question 8.
2x – y = 5
2y + x = -1
Answer:
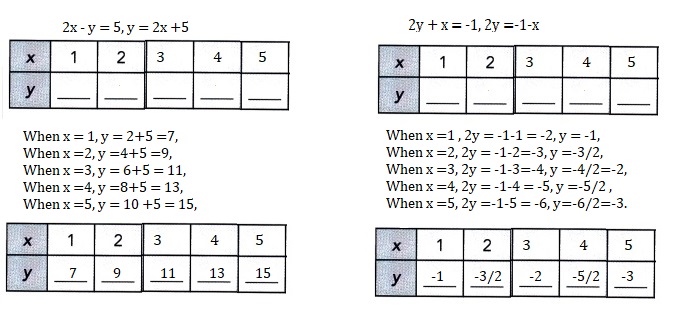
Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.
Question 9.
2x + y = -1
x + y = 1
Answer:
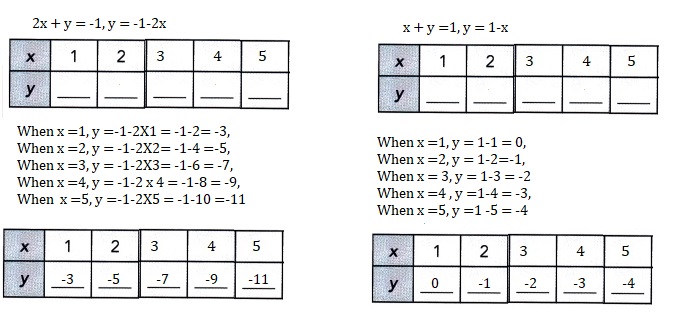
Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.
Solve by making a table of values. The values x and y are integers.
Question 10.
A shop sells a party hat at x dollars and a mask at y dollars.
On a particular morning, 10 hats and 20 masks were sold for $30.
In the afternoon, 8 hats and 10 masks were sold for $18. The related system of linear equations is:
10x + 20y =30
8x + 10y = 18
Solve the system of linear equations. Then find the cost of each hat and each mask.
Answer:
The cost of each hat is $1 and each mask is$1,
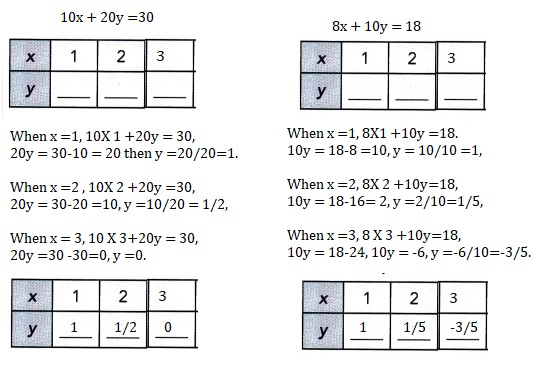
Explanation:
Given A shop sells a party hat at x dollars and a mask at y dollars.
On a particular morning, 10 hats and 20 masks were sold for $30.
In the afternoon, 8 hats and 10 masks were sold for $18.
The related system of linear equations is:
10x + 20y =30—(1)
8x + 10y = 18—-(2) dividing equation 1 by 10 we get
x +2y = 3,
x = 3-2y substituting in equation 2 we get
8(3-2y) +10y =18,
24 – 16y+10y =18,
24 -6y =18,
6y = 24 -18,
6y =6, y =1 we have x = 3-2X 1 = 3-2 = 1.
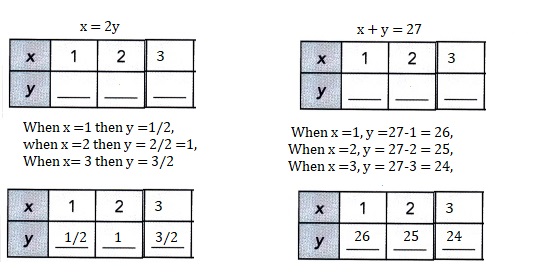
Question 11.
Alicia is x years old and her cousin is y years old.
Alicia is 2 times as old as her cousin.
Three years later, their combined age will be 27 years.
The related system of linear equations is:
x = 2y
x + y = 27
Solve the system of linear equations. Then find Alicia’s age and her cousin’s age.
Answer:
Alicia’s age is 18 and her cousin’s age is 9 years old,
Explanation:
GivenAlicia is x years old and her cousin is y years old.
Alicia is 2 times as old as her cousin.
Three years later, their combined age will be 27 years.
The related system of linear equations is: x = 2y,
x + y = 27 solving the equations 2y + y = 27,
3y = 27, y = 27/3 =9, so x = 2X 9 = 18, Alicia’s age is 18 and her
cousin’s age is 9 years old.
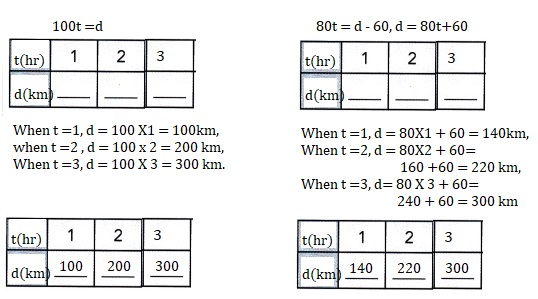
Question 12.
Steve and Alex start driving at the same time from Boston to Paterson.
The journey is d kilometers. Steve drives at 100 kilometers per hour and
takes t hours to complete the journey. Alex, who drives at 80 kilometers per hour is
60 kilometers away from Paterson when Steve reaches Paterson.
The related system of linear equations is:
100t = d
80t = d – 60
Solve the system of linear equations by making tables of values.
Then find the distance between Boston and Paterson.
Answer:
300 kilometers is the distance between Boston and paterson,
Explanation:
Given Steve and Alex start driving at the same time from Boston to Paterson.
The journey is d kilometers. Steve drives at 100 kilometers per hour and
takes t hours to complete the journey. Alex, who drives at 80 kilometers per hour is
60 kilometers away from Paterson when Steve reaches Paterson.
The related system of linear equations is:
100t = d
80t = d – 60 substituting 80t = 100t -60,
100t-80t = 60,
20t = 60, t = 60/20, t =3 so distance is 100 X 3= 300 kilometers.