This handy Math in Focus Grade 8 Workbook Answer Key Chapter 11 Lesson 11.1 Compound Events detailed solutions for the textbook questions.
Math in Focus Grade 8 Course 3 B Chapter 11 Lesson 11.1 Answer Key Compound Events
Math in Focus Grade 8 Chapter 11 Lesson 11.1 Guided Practice Answer Key
Tell whether the outcomes described are from a simple or compound event. If it is a compound event, identify the simple events that form the compound event.
Question 1.
Obtaining two heads when two coins are tossed
Answer:
There are two simple events each consisting of tossing a coin.
Thus it is a compound event
Question 2.
Winning a football game
Answer:
Simple event
Question 3.
Getting a number less than 4 or getting a number greater than 5 when a fair six-sided number die is rolled
Answer: Simple event
Question 4.
Rolling two fair six-sided number dice and obtaining a sum of 10 from the throws
Answer: There are two simple events each consisting of rolling a fair number die.
Represent and tell the number of possible outcomes for each compound event described.
Question 5.
Two fair coins are tossed together.
Answer:
The possibilities of tossing two coins are {(HH), (TT), (H,T), (T, H)}
Thus there are 4 outcomes of tossing two fair coins.
Question 6.
The results of rolling two fair six-sided number dice are multiplied.
Answer:
(1, 1), (1, 2) (1, 3), (1, 4) (1, 5) (1, 6)
(2, 1), (2, 2) (2, 3), (2, 4) (2, 5) (2, 6)
(3, 1), (3, 2) (3, 3), (3, 4) (3, 5) (3, 6)
(4, 1), (4, 2) (4, 3), (, 4) (4, 5) (4, 6)
(5, 1), (5, 2) (5, 3), (5, 4) (5, 5) (2, 6)
(6, 1), (6, 2) (6, 3), (6, 4) (6, 5) (6, 6)
The possible outcomes are 36.
Question 7.
A fair six-sided number die and a fair four-sided number die labeled 1 to 4 are rolled. The results that face down on both number dice are recorded.

Answer:
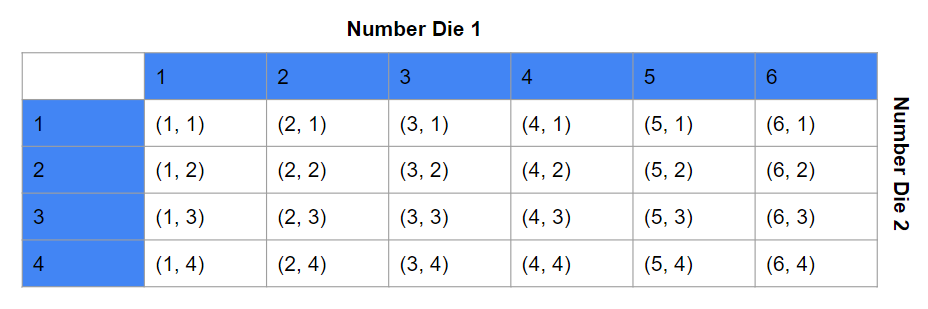
For each compound event, draw a tree diagram to represent the possible outcomes. Then tell the number of possible outcomes.
Question 8.
Joshua has two bags. In the first bag, there are 2 blue beads and 1 green bead. In the second bag, there are 3 lettered cards with the letters P, Q, and R. Joshua randomly takes an item from the first bag, and then from the second bag.
Answer:
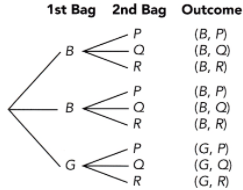
The possible outcomes are 9
Where,
B represents blue
G represents Green
P represents letter P
Q represents letter Q
R represents letter R
Question 9.
A fair coin is tossed then a fair four-sided color die with faces painted yellow, green, blue, and black is rolled. The color facing down is the result recorded.
Answer:
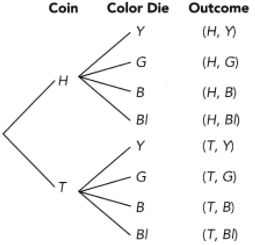
The possible outcomes are 8.
Where,
H represents heads
T represents tails
Y represents yellow
G represents green
B represents blue
B represents black
Math in Focus Course 3B Practice 11.1 Answer Key
Tell whether each statement is True or False.
Question 1.
Selecting letter A from the word PROBABILITY is a compound event.
Answer:
P – 1
R – 1
O – 1
B – 2
A – 1
I – 2
L – 1
T – 1
Y – 1
So, the statement is false.
Question 2.
Selecting letter B from the word BASEBALL and ABLE is a simple event.
Answer:
B – 2
A – 2
S – 1
E – 1
L – 2
The statement is false
ABLE is a simple event
Question 3.
Tossing a fair six-sided number die to get either an even number or a five is a compound event.
Answer:
Rolling an even number: {2, 4, 6}
Rolling a 5: {5}
The statement “Tossing a fair six-sided number die to get either an even number or a five is a compound event” is false.
Question 4.
Umberto has 3 red cards and 4 blue cards. Drawing two red cards in a row, without replacing the first card before drawing the second card, is a compound event.
Answer: true
Tell whether the outcomes described are from a simple or compound event. If it is a compound event, identify the simple events that form the compound event.
Question 5.
Getting a 6 when a fair six-sided number die is rolled.
Answer:
Rolling a 6: {6}
A simple event is an event with only one outcome.
Question 6.
Rolling three fair six-sided number dice and obtaining a sum of 18 from the throws.
Answer:
There are 3 possible outcomes.
A compound event is an event with more than one outcome.
Question 7.
Getting an eighteen when a fair twenty-sided number die is rolled.

Answer:
There is one possible outcome thus it is a simple event.
Question 8.
Susan has 3 red cards and 4 blue cards. She first draws a blue card. Without replacing the first card, she then draws another blue card.
Answer: Compound event
Solve. Show your work.
Question 9.
In the top drawer, there are two battery operated flash lights, one red and one yellow. In the second drawer, there are three packages of batteries: small, medium, and large. A flashlight and a package of batteries are randomly selected.
a) Use a possibility diagram to represent the possible outcomes.
Answer:
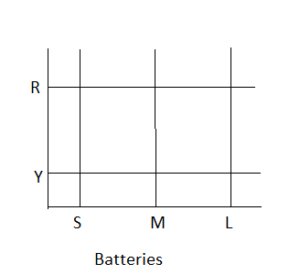
R represents red
Y represents yellow
S represents small
M represents medium
L represents large
b) How many possible outcomes are there?
Answer: 6 outcomes
Question 10.
Two electronic spinners, A and B, are spun by pressing a button. Spinner A has four sectors labeled 1 to 4, while B has three sectors, labeled 1 to 3. Spinner B, due to technical error, will never land on number 2 if spinner A lands on a 4.
a) Use a possibility diagram to represent the possible outcomes.
Answer:
The target of this task is to analyze the events of turning two spinners labelled t 2, 3, and 4, and 1, 2, and 3 then make a diagram that shows all its possibLe outcomes then determine the number of its possible outcomes given a condition of not being able to get (4, 2).
Since there are two spinners A and B, marked from 1 – 4 and 1 – 3 then the illustration for the possible outcomes would be as depicted in the table.
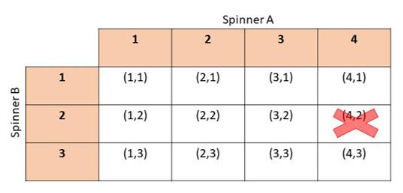
b) How many possible outcomes are there?
Answer:
The possible outcomes are (1, 1), (2, 1), (3, 1), (4, 1), (1, 2), (2, 2), (3, 2), (1, 3), (2, 3), (3, 3). and (4, 3)Therefore, there are 11 possible outcomes.
Question 11.
Winston has two boxes. The first box has 3 black pens and 1 red pen. The second box has 1 green ball and 1 yellow ball. Use a tree diagram to represent the possible outcomes for randomly drawing a pen and a ball. Then tell the number of possible outcomes.

Answer:
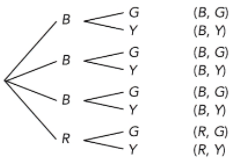
8 outcomes
R represents red
Y represents yellow
G represents green
B represents black
Question 12.
Seraphina first tosses a fair six-sided number die. She then tosses a fair coin. Use a tree diagram to represent the possible outcomes.
Answer:
The objective of this task is to make a tree diagram for the possibLe outcomes for tossing a number die and flipping a coin.
Observe that rolling a die has 6 possible outcomes, then start the tree diagram with 6 branches. Now, at the end of these branches put the possible outcomes: 1, 2, 3, 4, 5 and 6. Next in tossing a coin, since there are 2 possible outcomes then for each number, make another 2 branches. At the end of these branches put the possibLe outcomes: H for head and T for tail. Finally, conclude the possible results. The tree diagram for this event would be as depicted below.
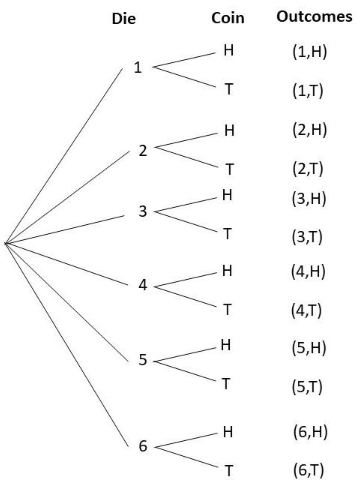
Question 13.
A game was designed such that a participant needs to accomplish 2 rounds to be considered the overall winner. The first round is to roll a 4 from a fair four-sided number die labeled 1 to 4. The result recorded is the number facing down. The second round is to randomly draw a red ball from a box of 2 differently colored balls.
a) Draw a tree diagram to represent the possible outcomes.
Answer:
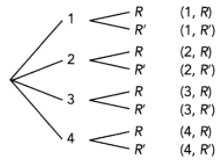
R represents red
R’ represents not red
b) How many possible outcomes are there?
Answer: 8 outcomes
c) Math Journal If the participant first draws the colored ball and then rolls the four-sided number die, will the number of possible outcomes be the same? Use a diagram to explain your reasoning.
Answer: Yes, there are still 8 outcomes
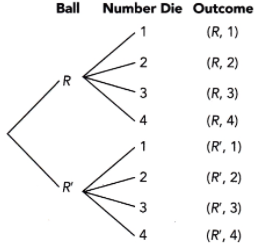
R represents red
R’ represents not red
Question 14.
Zoe first rolls a fair four-sided number die labeled 1 to 4. Then she rolls another fair four-sided number die labeled 2 to 5. The result recorded is the number facing down.

a) Use a possibility diagram to find the number of favorable outcomes for an odd sum.
Answer:
Note that there are 4 possible outcomes for born toss of the die, add these results, then the outcomes in tossing a die twice and adding their result would be as depicted in the table. Mark the sum that are odd.
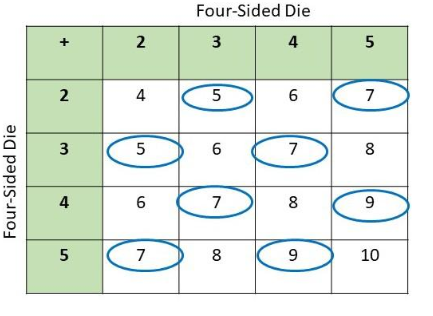
Observe that there are 16 possib[e outcomes and 8 are odd then

Therefore, the probability of obtaining an odd sum is \(\frac{1}{2}\).
b) Use a possibility diagram to find the number of favorable outcomes for a difference greater than 2.
Answer:
Since there are 4 possible outcomes for both toss of the die, subtract these results, then the outcomes in tossing a die twice and subtracting their result would be as depicted in the table. Mark the difference that are bigger than 2.
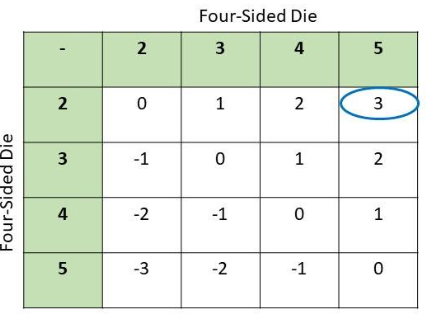
Notice that there are 16 possible outcomes and only 1 is larger than 2 then

Therefore, the probability of obtaining a difference greater than 2 is \(\frac{1}{16}\).