This handy Math in Focus Grade 8 Workbook Answer Key Chapter 9 Lesson 9.1 Understanding and Applying Congruent Figures detailed solutions for the textbook questions.
Math in Focus Grade 8 Course 3 B Chapter 9 Lesson 9.1 Answer Key Understanding and Applying Congruent Figures
Math in Focus Grade 8 Chapter 9 Lesson 9.1 Guided Practice Answer Key
Identify the figures that seem congruent. Explain why they seem so.
Question 1.
Answer: Figures A and F seems congruent because they have the same shape and same size.
Question 2.
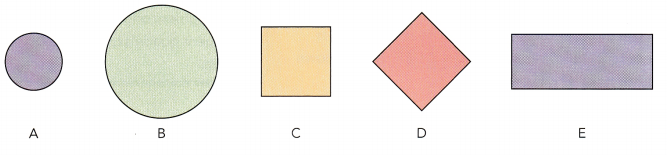
Answer: C and D seems congruent because they have the same shape and same size.
Complete.
Question 3.
The quadrilaterals below are congruent. Write the statement of congruence.
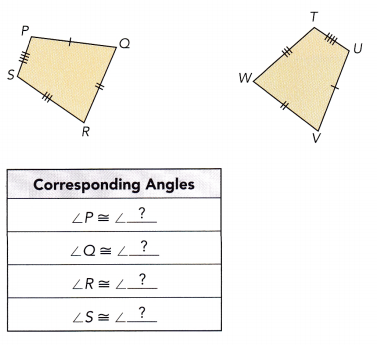
So, the statement of congruence is PQRS ≅ ____________.
Answer:
The corresponding angles from the above figure is
∠P = ∠U
∠S = ∠T
∠R = ∠W
∠S = ∠V
So, the statement of congruence is PQRS ≅ UTWV.
Question 4.
To make two congruent quadrilaterals, Wendy cut two pieces of cardboard, one on top of the other. She measured the lengths of some sides of the quadrilaterals.
a) Find the values of the variables x, y, and z. All lengths are in inches.
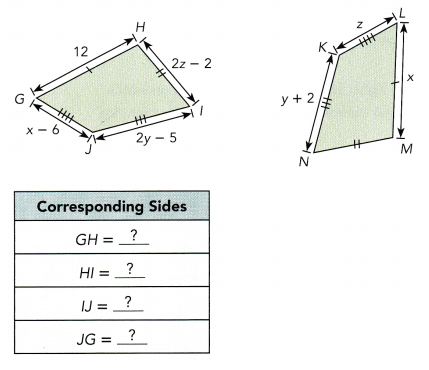
Solve for x:
x = 
LM =
Solve for y.
2y – 5 = IJ =
2y – 5 + 5 = Add 5 to both sides.
2y = Simplify.
2y – y = Subtract y from both sides.
y = Simplify.
Solve for z:
x – 6 = JG =
– 6 = Substitute x = .
= z Simplify.
So, the value of x is , y is , and z is .
Answer:
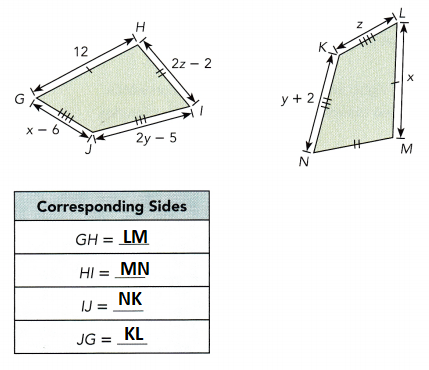
Solve for x:
x = 12 LM = 12
Solve for y.
2y – 5 = y + 2 IJ = NK
2y – 5 + 5 = y + 2 + 5 Add 5 to both sides.
2y = y + 7 Simplify.
2y – y = 7 Subtract y from both sides.
y = 7 Simplify.
b) What is the length of each side of GHIJ? of NKLM?
GH = in., HI = in., IJ = in., JG = in.
NK = in., KL = in., LM = in., MN = in.
Answer:
GH = 12 in., HI = 10 in., IJ = 7 in.,
JG = in.
x – 6 = z
12 – 6 = z
z = 6
NK = 7 in., KL = 6 in., LM = 12 in.,
MN = 10 in.
2z – 2 = 2 (6) – 2 = 12 – 2 = 10
Technology Activity
Materials:
geometry software
OBSERVE THE CONGRUENCE IN TRIANGLES
STEP 1: Draw △ABC and △DEFso that m∠CAB m∠FDE, AB = DE, and AC = DF. Draw the two triangles such that point A is 10 units to the left of point D.
STEP 2: Translate △ABC 10 units to the right. Select the Translate function within the Transform menus. Do the two triangles overlap? Are the two triangles congruent?
STEP 3: Repeat STEP 1 and STEP 2 for triangles with different dimensions. Which pairs of corresponding parts did you specify to be congruent? Was this sufficient to make the triangles congruent?
STEP 4: Repeat STEP 1 to STEP 3 with △ABC and △DEF so that m∠CAB = m ∠FDE, AB = DE, and m∠CBA = m∠FED.
STEP 5: Repeat STEP 1 to STEP 3 with △ABC and △DEF so that BC = EF, AB = DE, and AC = DF.
STEP 6: Repeat STEP 1 to STEP 3 with △ABC and △DEF so that m∠CAB = m ∠FDE = 90°, BC = EF, and AC = DF.
Math Journal How are △ABC and △DEF related in each case? What are the four sets of the minimum conditions for two triangles to be congruent?
Answer:
Question 5.
Justify whether the triangles are congruent. If they are congruent, write the statement of congruence and state the test used.
a)
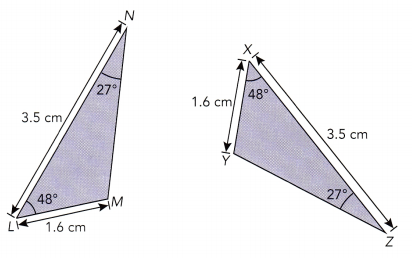
LN = , m∠ = m∠, and LM = .
By the SAS test, △LMN ≅ .
Caution
In the SAS test, the angle congruent to its corresponding angle must be the included angle, which is the angle between the congruent corresponding sides.
Answer:
LN = XZ, m∠ = NML = m∠YXZ, and LM = XY.
By the SAS test, △LMN ≅ △XYZ.
b)
m∠ABE = m∠ Corr. ∠s
m∠BAE = m∠ Corr.∠s
m∠AEB = m∠ ∠sum of triangle
Three pairs of congruent angles do not ensure that the triangles are .
Answer:
m∠ABE = m∠BCD Corr. ∠s
m∠BAE = m∠CBD Corr.∠s
m∠AEB = m∠BDC ∠sum of triangle
Three pairs of congruent angles do not ensure that the triangles are CONGRUENT.
Math in Focus Course 3B Practice 9.1 Answer Key
Name the figures that are congruent. Name the corresponding congruent line segments and angles.
Question 1.
ABCD is a parallelogram with diagonal \(\overline{B D}\).
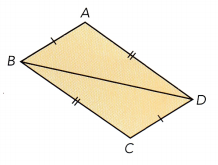
Answer: Yes the above parallelogram is congruent (△BAD ≅ △DCB).
AB = CD and AD = BC because opposite sides of a parallelogram are equal.
∠ABD = ∠CDB And ∠BAD = ∠DCB
Question 2.
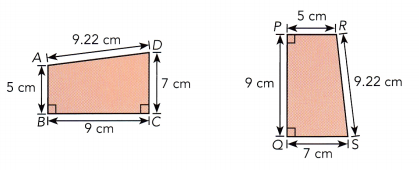
Answer:
ABCD ≅ PQRS
AB = PR = 5 cm
AD = RS = 9.22 cm
BC = PQ = 9 cm
DC = QS = 7 cm
∠ABC = ∠RPQ
∠DCB = ∠SQP
Solve. Show your work.
Question 3.
WXYZ is a rectangle with diagonal \(\overline{W Y}\). Explain, using the given test for congruent triangles, why △WXY is congruent to △YZW.
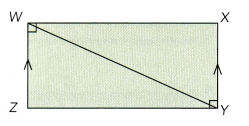
a) SSS
Answer: WX = ZY
WZ = XY
WY = WY
b) SAS
Answer:
WX = ZY
m∠ZWX= m∠ZYX
WZ = XY
c) ASA
Answer:
m∠ZWY= m∠XYW
d) HL
Answer:
ΔWXY = ΔWZY (right angled triangle)
WY = WY (Hypotenuse)
Question 4.
ABCDE is a regular pentagon with congruent diagonals \(\overline{B E}\) and \(\overline{B D}\).
a) Justify △ABE ≅ △CBD with a test for congruent triangles.
Answer:
We can test whether the given figures are congruent by testing SSS, ASA, SAS, and HL.
SSS test:
AB = BC
AE = CD
BE = BD
b) Name a pair of congruent quadrilaterals.
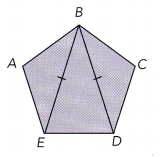
Answer: △ABE ≅ △CBD because the shape and size are equal.
Question 5.
△ABC is congruent to △PQR. Find the values of x, y, and z.
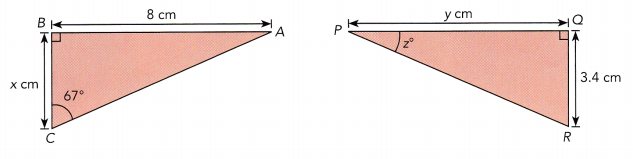
Answer:
Given,
△ABC is congruent to △PQR.
AB = PQ
BC = QR
AC = PR
AB = 8 cm
So, PQ = y = 8 cm
BC = x cm
We know that
BC = QR
So, BC = 3.4 cm
m∠BCA= m∠QPR
m∠BCA= 67°
So, m∠QPR = 67°
Question 6.
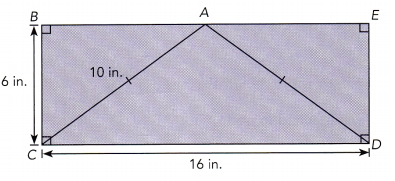
a) Name the figure that is congruent to trapezoid BADC.
Answer: The figure that is congruent to trapezoid BADC is AECD.
b) Find the length of each side of the trapezoid you named in a).
Answer:
From the figure, we can see that
BC = ED
AC = AD
BE = CD
Now we will find the unknown values of the figure.
BC = 6 in.
So, ED = 6 in.
AC = 10 in.
AC = AD = 10 in.
BE = CD
CD = 16 in
So, BE = CD = 16 in.
Question 7.
A piece of fabric has many printed shapes of congruent triangles and congruent quadrilaterals on it.
a) The pieces of fabric shown are congruent quadrilaterals. Find the value of x, y, and z.
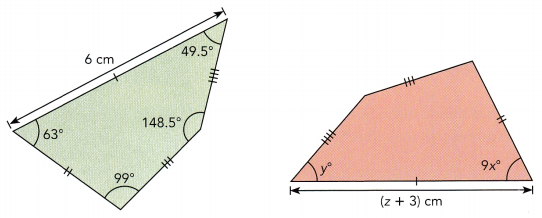
Answer:
z + 3 = 6 cm
z = 6 – 3
z = 3 cm
9x° = 63°
x° = 63/9
x = 7
y° = 49.5
b) The pieces of fabric shown are congruent triangles. Find the value of p, q, and r.
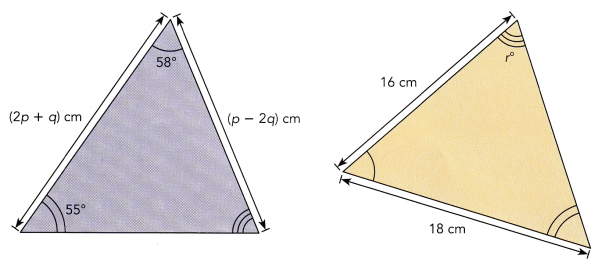
Answer:
2p + q = 18 cm—- eq. 1
p – 2q = 16 cm—-eq. 2
2p + q = 18 cm—- eq. 1 × 2
4p + 2q = 36 cm
p – 2q = 16 cm
5p = 52 cm
p = 52/5
p = 10.4 cm
substitute the value of p in the eq.2
10.4 – 2q = 16 cm
10.4 – 16 = 2q
-5.6 = 2q
q = -5.6/2
q = -2.8 cm
The sum of all three angles = 180°
55° + 58° + r° = 180°
113° + r° = 180°
r° = 180° – 113°
r° = 67°
Question 8.
The origami cornflower is formed by making symmetrical folds in a paper square. In the diagram, AB = BC = DE = EF and OA = OC = OD = OF. Write two possible statements of congruence for ABCO.
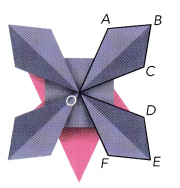
Answer:
△ABO and △BCO seems congruent
AB = BC.
Question 9.
In making this suspension bridge, engineers connected two cables at the same point P on the concrete piers and at the same distance from the base of the concrete piers at R.
a) Which congruence test ensures that △PQR is congruent to △PSR? Explain.
Answer: SAS (Side Angle Side). Each triangle in the below figure is a right angled triangle at R and congruent with the same size and shape.
b) How many other pairs of congruent triangles are attached to each concrete pier? Explain.
Answer: There are 10 pairs of congruent triangles that are attached to each concrete pier.
Question 10.
This skyscraper has several symmetric triangles overlaid on a grid of horizontal and vertical lines. In each direction, these lines are parallel.
a) This face of the building is symmetric about \(\overline{G K}\), so AB = CD, AX = CX, and BX = DX. Give the statement of congruence for △ABX and tell which congruence test you used.
Answer: SSS test is used to tell whether the figure is congruent. △ABX ≅ △CDX
b) Is △EFG congruent to △HJK? Explain.
Answer: No because the shape of the triangles is same but the size of the triangles are different.