Math in Focus Grade 8 Chapter 9 Lesson 9.2 Answer Key Understanding and Applying Similar Figures

This handy Math in Focus Grade 8 Workbook Answer Key Chapter 9 Lesson 9.2 Understanding and Applying Similar Figures detailed solutions for the textbook questions.

Math in Focus Grade 8 Course 3 B Chapter 9 Lesson 9.2 Answer Key Understanding and Applying Similar Figures

Math in Focus Grade 8 Chapter 9 Lesson 9.2 Guided Practice Answer Key

Identify the figures that seem similar. Explain why.

Question 1.

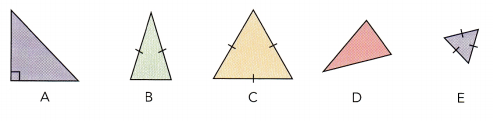
Answer: A and E are the similar triangle because all the sides are equal. The shape of A and E are the same but the size is different.

Hands-On Activity

Materials

• ruler
• scissors

EXPLORE ANGLE MEASURES IN SIMILAR TRIANGLES

STEP 1: Draw an acute-angled triangle. Name the angle at each vertex A, B, and C as shown below. Draw a line segment parallel to \(\overline{B C}\). Name the line segment \(\overline{D E}\).

STEP 2: Cut △ABC along its edges. Then cut the triangle along \(\overline{D E}\). You should have one small triangle, △ADE, and a trapezoid, BDEC.

STEP 3: Place ∠B on top of the angles in A ADE, one by one. Which angle has the same measure as ∠B?

STEP 4: Place ∠C on top of the angles of △ADE, one by one. Which angle has the same measure as ∠C?

STEP 5: In the diagram in STEP 1, \(\overline{D E}\) and \(\overline{B C}\) are parallel and intersected by \(\overline{A B}\) and \(\overline{A C}\). What do you know about angle measures formed when a line intersects two parallel lines? How does this fact support what you saw in STEP 3 and STEP 4?

Math Journal Triangles ADE and ABC are similar because they have the same shape but not the same size. In these triangles, △ADE and AABC are called corresponding angles. Two other pairs of corresponding angles are angles AED and ACB and angles DAE and BAC. What did you observe about the measures of each pair of corresponding angles?
Answer: ∠B and ∠D are the corresponding angles.
∠E and ∠C are the corresponding angles.

Solve.

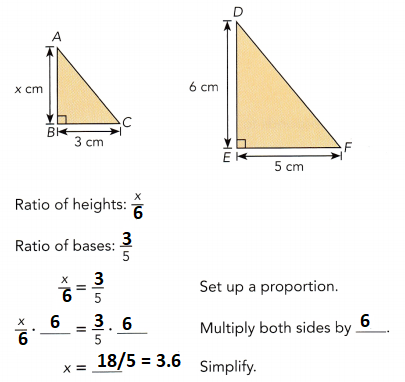
Question 2.
Triangle ABC and triangle DBF are similar triangles. Find the value of x.

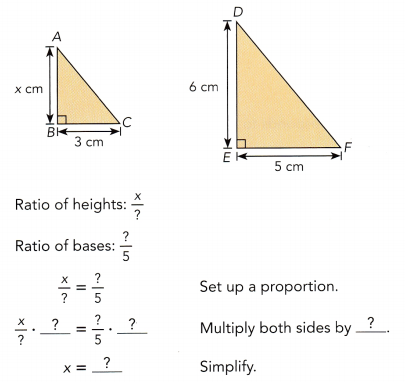
Answer:

Question 3.
An engineer wants to make a bridge across a river at \(\overline{P R}\). The diagram shows the known measurements. \(\overline{S P}\) and \(\overline{T R}\) are straight lines and triangle RPQ is similar to triangle TSQ. Find the width x of the river.

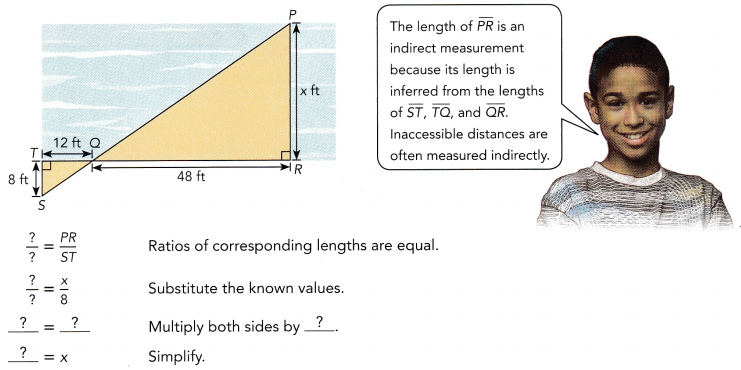
The width of the river is feet.
Answer:

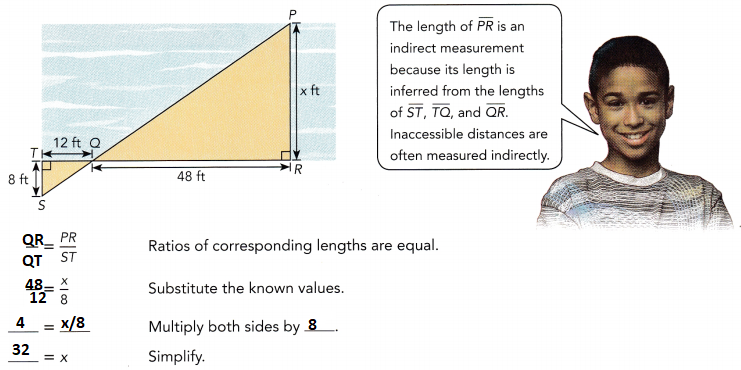
The width of the river is 32 feet.

Question 4.
△ABC and △DEF are similar triangles. Find m∠D, m∠E, and m∠F.

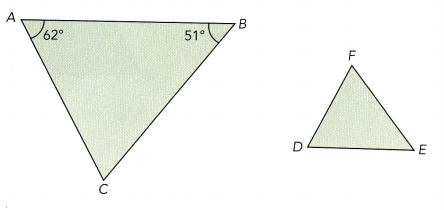
The corresponding angles of similar triangles have measures.
So m∠D = m∠ = ,
m∠E = m∠ = ,
and m∠F = 180° – – ∠ sum of triangle
= .
Answer:
The corresponding angles of similar triangles have same or equal measures.
So m∠D = m∠A = 62°,
m∠E = m∠B = 51°,
and m∠F = 180° – 62° – 51° ∠ sum of triangle
m∠F = 67°

Question 5.
The area of △AXY is 12 square centimeters. Find the area of △ABC.
Use the ratio of corresponding lengths to find the ratio of the areas.

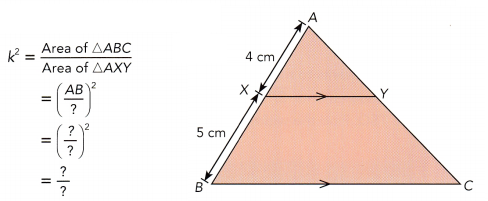
Let the area of △ABC be x square centimeters.
Use the ratio of the areas to find x.
\(\frac{x}{12}\) = k² The ratio of the areas equals k².
\(\frac{x}{12}\) = \(\frac{?}{?}\) Substitute for k²,
\(\frac{x}{12}\) • 12 = \(\frac{?}{?}\) • Multiply both sides by .
x = Simplify.
The area of △ABC is square centimeters.
Answer:

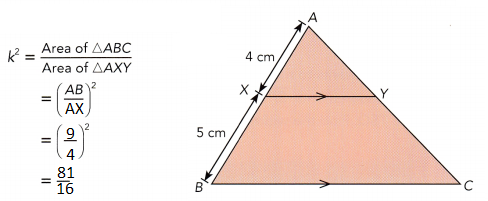
\(\frac{x}{12}\) = k² The ratio of the areas equals k².
\(\frac{x}{12}\) = \(\frac{81}{16}\) Substitute 81/16 for k²,
\(\frac{x}{12}\) • 12 = \(\frac{81}{16}\) • 12 Multiply both sides by 12.
x = 60.75 Simplify.
The area of △ABC is 60.75 square centimeters.

Hands-On Activity

Materials:

• two similar triangles
• protractor
• ruler

EXPLORE A MINIMUM CONDITION FOR TWO SIMILAR TRIANGLES

STEP 1: Measure the side lengths of the triangles. Find out if △ABC is similar to △PQR by finding the ratios of the corresponding side lengths.

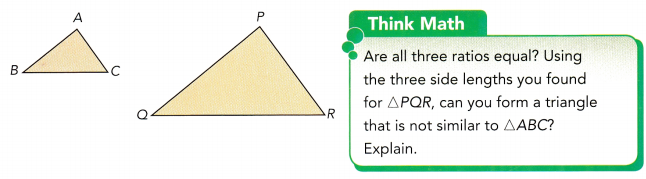
STEP 2: Measure ∠A, ∠B, ∠P, and ∠Q. Complete the following:
m∠A = m∠ and m∠B = m∠.

Math Journal Without measuring ∠C and ∠R, do you know whether they have the same measure? Explain. State a minimum condition for two triangles to be similar.
Answer:
m∠A = m∠p and m∠B = m∠Q.

Identify whether △ABC is similar to △DEF. Explain with a test for similar triangles.

Question 6.

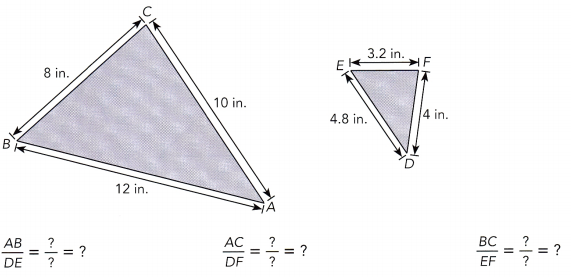
All three pairs of corresponding side lengths have the ratio.
So, △ABC △DEF.
Answer:

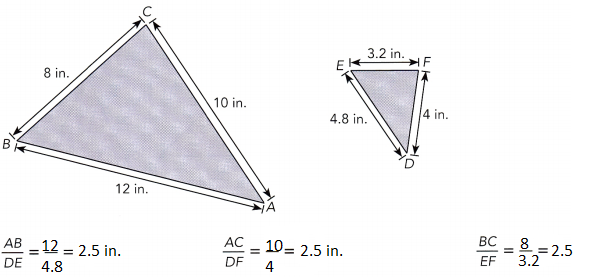
All three pairs of corresponding side lengths have the same ratio.
So, △ABC ≈ △DEF.

Question 7.

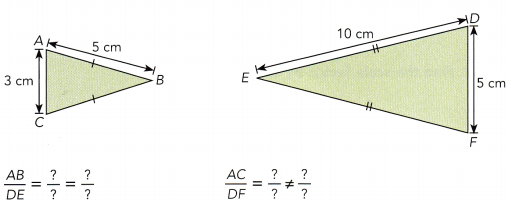
Two pairs of corresponding side lengths have ratios.
So, △ABC △DEF.
Answer:

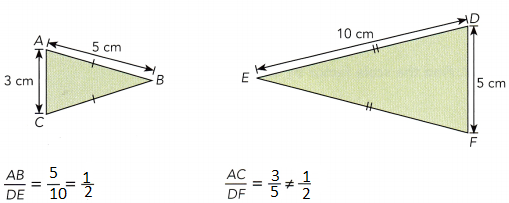
Two pairs of corresponding side lengths have different ratios.
So, △ABC are not similar to △DEF.

Question 8.

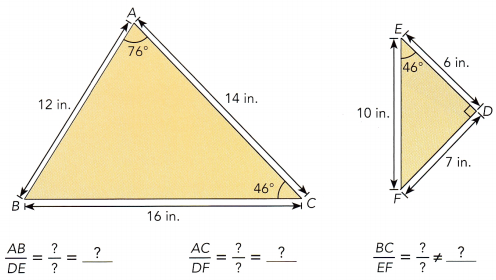
m∠BAC ≠ m∠
Two pairs of corresponding side lengths have the ratio and the included angles have measures.
So, △ABC △DEF.
Answer:

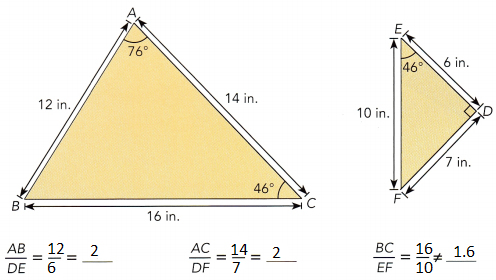
m∠BAC ≠ m∠DEF
Two pairs of corresponding side lengths have the different ratio and the included angles have different measures.
So, △ABC is not similar to △DEF.

Math in Focus Course 3B Practice 9.2 Answer Key

Identify the figures that seem similar. Explain why.

Question 1.

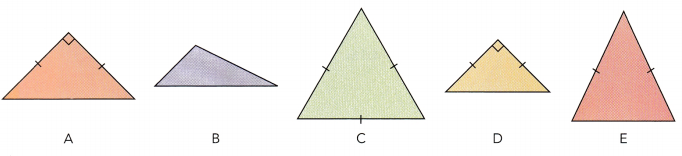
Answer:
A and D are similar figures with the same shape.

Question 2.

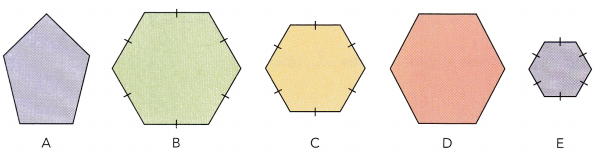
Answer: B, C and D are similar figures with a similar shape.

Triangle ABC is similar to triangle POR. Find the scale factor by which △ABC is enlarged to △PQR.

Question 3.

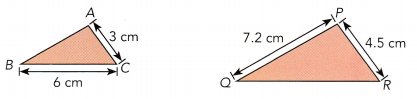
Answer:
Scale factor = scale/actual length
Scale factor = 4.5/3 = 1.5

Question 4.

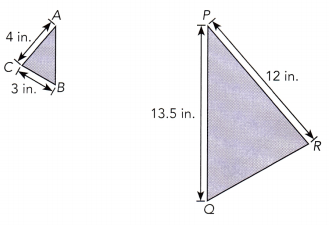
Answer:
Scale factor = scale/actual length
Scale factor = 12/4 = 3

Question 5.

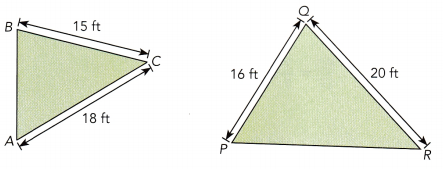
Answer:
Scale factor = scale/actual length
Scale factor = 20/15 = 4/3 = 1 1/3

Each pair of figures are similar. Find the value of each variable.

Question 6.
ABCD ~ EFGH

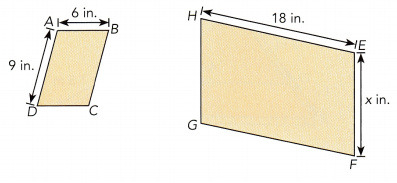
Answer:
By seeing the above figures we can say that it is a parallelogram.
We know that the opposite sides of the parallelogram are equal.
AB = 3EF
AD = 3EH
AB = 6 in.
EF = 3 × 6 in = 18 in.
AD = 9 in.
EF = 3x = 3 × 9 = 27 in.
Thus the value of x is 6 in.

Question 7.
△ABC ~ △DEF

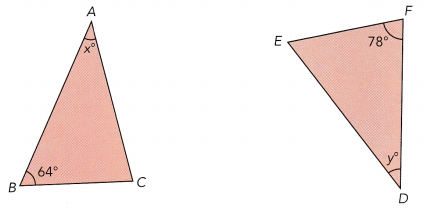
Answer:
As the given triangles are similar the angles will be same.
∠B = 64°
∠C = 78°
Sum of angles = 180°
∠x° + 64° + 78° = 180°
∠x° = 180° – 64° – 78°
x° = 38°
x° = y° = 38°

Question 8.
ABCD ~ EFGH

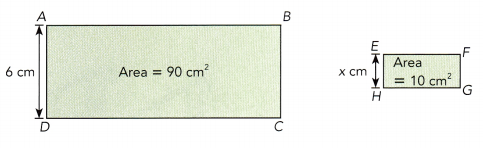
Answer:
90/6 = 10/x
9/6 = 1/x
x × 9 = 6
x = 6/9
x = 2/3

Question 9.
△ABC ~ △DEF

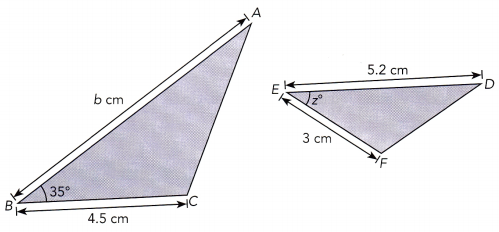
Answer:
AB = ED
BC = EF
AC = DF
BC/EF = 4.5/3 = 1.5
Scale factor = 1.5
AD = 5.2 cm
AB = 5.2 × 1.5 = 7.8
z° = 35°

Explain, with a test, why the two triangles in each figure are similar. Find the unknown lengths.

Question 10.

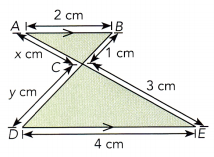
Answer:
By using the SSS test we can say that the two triangles are similar because the shape of two triangles are same.
AB = DE
AC = CE
BC = CD
AB = 2 cm
DE = 4 cm
scale factor = 4/2 = 2
BC = 1 cm
CD = 1 × 2 = 2 cm
CD = y = 2 cm
CE = 3 cm
CE = 3/2 = 1.5 cm
x = 1.5 cm

Question 11.

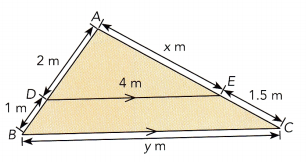
Answer:
AB = AE
2 + 1 = 3 m
So, AE = x = 3 m
AD + DE = BC
2 + 4 = 6m
Thus x = 3 and y = 6

Solve. Show your work.

Question 12.
Mia made some copies of a drawing using a photocopier. The drawing was either enlarged or reduced. Find the value of x.
a)

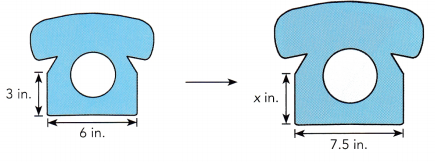
Answer:
7.5/6 = 1.25
3 × 1.25 = 3.75 in.
Thus the value of x is 3.75 in.

b)

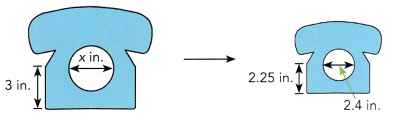
Answer:
3/2.25 = 1.3 in
x = 2.4 × 1.3 = 3.12 in
Thus the value of x is 3.12 in.

Question 13.
The slope of a wheelchair ramp is \(\frac{1}{15}\).

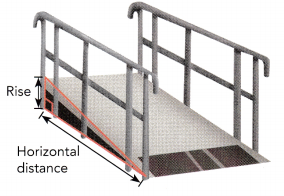
a) Suppose a wheelchair ramp has to rise 3 feet. Find the horizontal distance it covers.
Answer:
3/x = 1/15
3 × 15 = x
x = 45 feet
Thus the horizontal distance it covers is 45 feet.

b) Suppose there is space for a wheelchair ramp to cover at most 30 feet horizontally. How high can it rise then?
Answer:
x/30 = 1/15
x = 30/15
x = 2
Thus it rise 2 feet.

Question 14.
A circle has 9 times the area of another circle. If the radius of the larger circle is 27 meters, find the radius of the smaller circle.
Answer:
Given,
A circle has 9 times the area of another circle.
Radius of the larger circle is 27 meters.
Area of circle (A1) = 9 Area of circle2(A2)
A1 = 9A2
We know that,
Area of the circle = πr²
where r is the radius of the circle
r1 = 27 meters
r2 = ?
A1 = πr²
A1 = 3.14 × r²
A1 = 9A2
π(27)² = 9πr²
r² = (27)² /9
r = 27/3
r2 = 9 meters
Thus the radius of the smaller circle = 9 meters

Question 15.
The two ellipses shown on the right are similar. The area of the inner ellipse is 18 square inches and the shaded area is 32 square inches. Find the values for x and y.

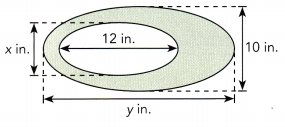
Answer:
Given,
The area of the inner ellipse is 18 square inches.
a = 12/2 = 6 in.
18 = 6 × b
18/6 = b
b = 3
x = 3 + 3
x = 6 in.

Question 16.
Two trees on a street have heights 10 feet and 28 feet. At a certain time of a day, the shorter tree casts a shadow of length 15 feet on the ground. How far apart are the trees?

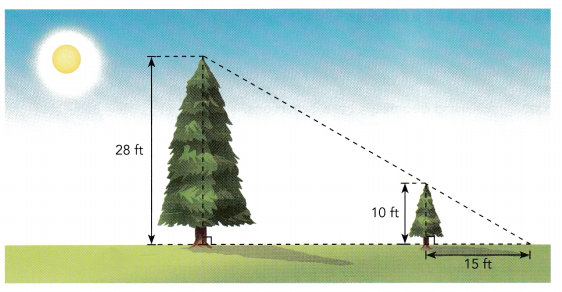
Answer:
Given,
Two trees on a street have heights 10 feet and 28 feet.
At a certain time of the day, the shorter tree casts a shadow of length 15 feet on the ground.
Let x be the distance between the two trees.
x + 15
10 : 28 = x : x + 15
10/28 = x/x + 15
10(x + 15) = x × 28
10x + 150 = 28x
150 = 28x – 10
18x = 150
x = 150/18
x = 8.3
x + 15 = 8.3 + 15 = 23.3 feet

Question 17.
A bag in the shape of two regular pentagons is shown on the right. The ratio of the shaded area to the area of the larger pentagon is 27 : 36. If the larger pentagon has sides of length 4 inches, find the length of the sides of the smaller pentagon.

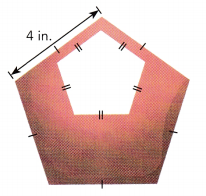
Answer:
Given,
A bag in the shape of two regular pentagons is shown on the right.
The ratio of the shaded area to the area of the larger pentagon is 27 : 36.
Larger pentagon has sides of length 4 inches
Let the length of the sides of the smaller pentagon be x.
27/36 = x/4
3/4 = x/4
(3 × 4)/4 = x
x = 12/4
x = 3
Thus the length of the sides of the smaller pentagon is 3 inches.

Question 18.
A cable car travels from a village up to a resort on the top of a mountain. When the cable car has traveled 150 feet along the cable, it is 100 feet above the ground. The total distance the cable car must travel to reach the resort is 12,000 feet. How high is the mountain?

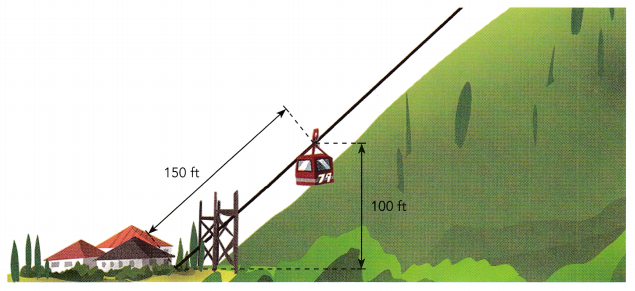
Answer:
Given that,
A cable car travels from a village up to a resort on the top of a mountain. When the cable car has traveled 150 feet along the cable, it is 100 feet above the ground.
The total distance the cable car must travel to reach the resort is 12,000 feet.
12000 ÷ 150 = 80
100 × 80 = 8000 feet
Thus the height of the mountain is 8000 feet.

Question 19.
Math journal Are similar figures ever congruent? If so, under which conditions are they congruent? Use two congruent triangles and two similar triangles in your explanation.
Answer:
Similar figures are not congruent until the scale factor is 1 or -1. The two triangles are said to be similar when all the three pairs of the figure are corresponding sides have the same ratio. If the ratio of the scale factor is 1 or -1 then the corresponding lengths are the same. When all the three pairs of corresponding lengths are the same then the triangle is said to be congruent.

Question 20.
Math journal Do you know all circles are similar? What other geometric shapes are similar?
Answer:
All circles are said to be similar because the radii are equidistant from their center.
Two shapes are said to be similar if and if it has the same shape but not the same size.