This handy Math in Focus Grade 8 Workbook Answer Key Chapter 9 Lesson 9.3 Relating Congruent and Similar Figures to Geometric Transformations detailed solutions for the textbook questions.
Math in Focus Grade 8 Course 3 B Chapter 9 Lesson 9.3 Answer Key Relating Congruent and Similar Figures to Geometric Transformations
Math in Focus Grade 8 Chapter 9 Lesson 9.3 Guided Practice Answer Key
Solve.
Question 1.
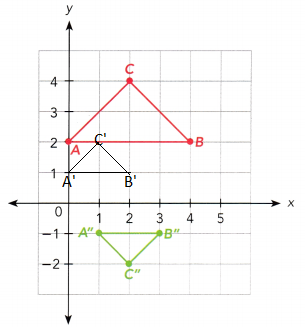
△ABC and △A’B’C’ are congruent isosceles triangles. Describe a rotation that maps △ABC onto △A’B’C’.
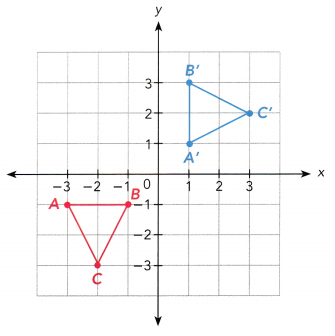
Answer:
Complete each 
with a value or word and each 
with +, —, x, or ÷.
Question 2.
△JKL is dilated by a scale factor of 1.2 to form △J’K’L’.
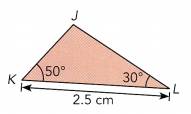
a) Find m∠J’.
△JKL and △J’K’L’ are triangles.
So, m∠J’ = m∠
– 50° – 30° = ∠ sum of triangle
m∠J’ is
Answer:
△JKL and △J’K’L’ are similar triangles.
So, m∠J’ = m∠J
180° – 50° – 30° = 100° ∠ sum of triangle
m∠J’ is 100°
b) Find the length of \(\overline{K^{\prime} L^{\prime}}\).
K’L’ = 2.5 1.2
= cm
Answer:
K’L’ = 2.5 × 1.2
We have to multiply the length with the scale factor to find the scaled length of \(\overline{K^{\prime} L^{\prime}}\).
= 3 cm
Question 3.
△UVW undergoes a geometric transformation to form △XYZ.
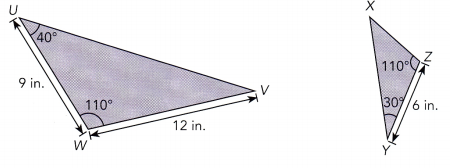
a) Identify whether △UVW ~ △XYZ.
m∠V 180° – – ∠ sum of triangle
=
Since m∠W = m∠Z and m∠V = m∠, two pairs of corresponding angles have equal measures. So, △UVW is to △XYZ.
Answer:
m∠V 180° – 110° – 40° ∠ sum of triangle
= 30°
Since m∠W = m∠Z and m∠V = m∠Y, two pairs of corresponding angles have equal measures. So, △UVW is ∼ to △XYZ.
b) If △UVW ~ △XYZ, what is the geometric transformation and scale factor?
Scale factor = \(\frac{Y Z}{?}\)
= \(\frac{6}{?}\)
=
△UVW undergoes a by a scale factor to form △XYZ.
Answer:
Scale factor = \(\frac{Y Z}{WV}\)
= \(\frac{6}{12}\)
= \(\frac{1}{2}\)
△UVW undergoes a dilation by a scale factor \(\frac{1}{2}\) to form △XYZ.
Copy and complete.
Question 4.
An engineer designs a manufacturing machine to transfer a food package GHIJ onto G’H’I’J’. Describe a sequence of two transformations that maps GHIJ onto G’H’l’J’.
GHIJ is mapped onto G’H’l’J’ by a translation of 2 units up and a reflection in the line .
Think Math
Does the order in which you do the transformations affect the image in Example 11 ? in 4?
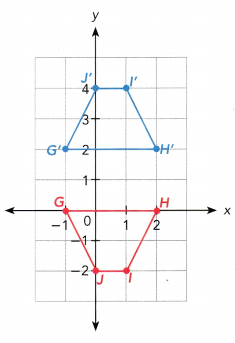
Answer:
GHIJ is mapped onto G’H’l’J’ by a translation of 2 units up and a reflection in the line 2.
Technology Activity
Materials
geometry software
EXPLORE SEQUENCES OF TRANSFORMATIONS
STEP 1: Draw a triangle on a coordinate system using a geometry software. Record the position of each vertex.
STEP 2: Translate the triangle 1 unit down. Then reflect it in the x-axis. Select the Translate function and Reflect function, within the Transform menus. Record the position of each vertex of the image triangle.
STEP 3: Change the order of transformations in STEP 2. Record the position of each vertex of this image triangle.
STEP 4: Draw another triangle on a coordinate system using a geometry software. Record the position of each vertex.
STEP 5: Translate the triangle 1 unit to the right. Then dilate it with the center at the origin and scale factor 2. Select the Translate function and Dilate function, within the Transform menus. Record the position of each vertex of the image triangle.
STEP 6: Change the order of transformations in STEP 5. Record the position of each vertex of this image triangle.
Math journal Compare the positions of the original and transformed triangles. Does the order in which you perform two transformations make a difference in the position of the image triangle? Explain.
Answer:
Copy and complete on a graph paper.
Question 5.
DEFG is mapped onto D’E’F’G’ under a transformation. D”E”F”G” is the image of D’E’F’G’ under another transformation.
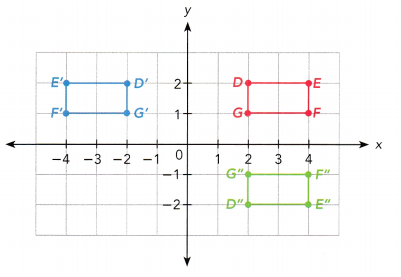
a) Describe the transformations that map DEFG onto D’E’F’G’ and D’E’F’G’ onto D”E”F”G”. Then describe a single transformation that maps DEFG onto D”E”F”G”.
DEFG is mapped onto D’E’F’G’ by using a reflection in the . D’E’F’G’ is mapped onto D”E”F”G” by using a rotation of about the origin. DEFG is mapped onto D”E”F”G” by using a single transformation, which is .
Answer:
DEFG is mapped onto D’E’F’G’ by using a reflection in the y-axis. D’E’F’G’ is mapped onto D”E”F”G” by using a rotation of 180 degrees about the origin. DEFG is mapped onto D”E”F”G” by using a single transformation, which is reflection in the x-axis.
b) Suppose the order of the transformations is reversed. Draw DEFG, D’E’F’G’, and D”E”F”G” on a coordinate plane. Does the order of the transformations affect the position of D”E”F”G”?
Answer: No, the order of the transformations affects the position of D”E”F”G” if you change the position in the y-axis.
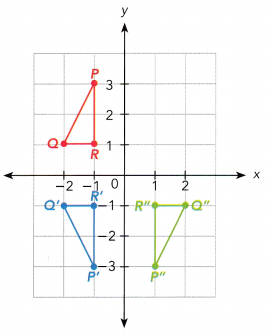
Question 6.
△PQR is mapped onto △P’Q’R’ under a transformation. △P”Q”R” is the image of △P’Q’R’ under another transformation.
a) Describe the transformation that maps △PQR onto △P’Q’R’ and △P’Q’R’ onto △P”Q”R”.
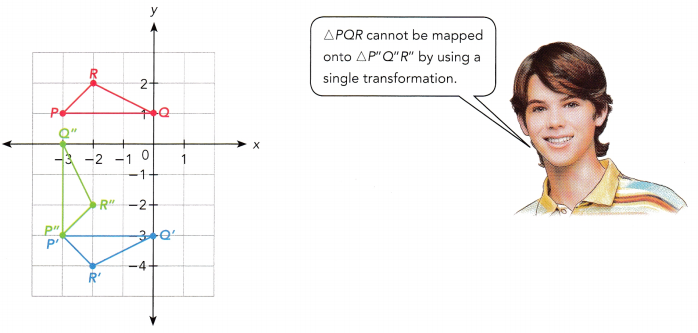
Answer: △PQR is mapped on to △P’Q’R’ by the reflection in the line y = -1 and △P’Q’R’ is mapped onto △P”Q”R” on a coordinate plane by using the anticlockwise rotation of 90 degree about (-3, -3)
b) Suppose the order of the transformations is reversed. Draw △PQR, △P’Q’R’, and △P”Q”R” on a coordinate plane. Does the order of the transformations affect the position of △P”Q”R”?
Answer:
Question 7.
△PQR is mapped onto △P’Q’R’ under a transformation. △P”Q”R” is the image of △P’Q’R’ under another transformation.
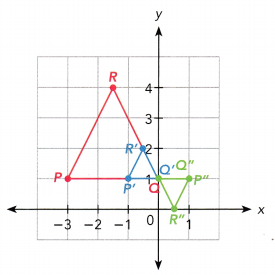
a) Describe the transformations that map △PQR onto △P’Q’R’ and △P’Q’R’ onto △P”Q”R”. Then describe a single transformation that maps △PQR onto △P”Q”R”.
△PQR is mapped onto △P’Q’R’ by using a dilation with center (, ) and scale factor . △P’Q’R’ is mapped onto △P”Q” R” by using a rotation of about the point (, ) . △PQR can be mapped onto △P”Q”R” by a single dilation with center (imgg 2, ) and scale factor .
Answer:
△PQR is mapped onto △P’Q’R’ by using a dilation with center (0, 1) and scale factor 1. △P’Q’R’ is mapped onto △P”Q” R” by using a rotation of 180 degrees about the point (0, 1) . △PQR can be mapped onto △P”Q”R” by a single dilation with center (imgg 2, 1) and scale factor 1.
b) If the order of transformations is reversed, draw △PQR, △P’Q’R’, and △P”Q”R” on a coordinate plane.
Answer:
Math in Focus Course 3B Practice 9.3 Answer Key
State whether the figure and image are congruent or similar.
Question 1.
A triangle is rotated 180° about the origin.
Answer: If a triangle is rotated 180° about the origin then the figure is congruent.
Question 2.
A pentagon is translated 1 unit to the left and 5 units up.
Answer: Similar figure
Question 3.
A projector dilates a picture by a scale factor of 10, and projects the image on a screen.
Answer: Similar figure
Question 4.
A parallelogram is dilated with center (-2, 4) and scale factor 3.5, and rotated 90° clockwise.
Answer: Similar figure
Question 5.
A cartoon character is reflected in the y-axis and translated to the right.
Answer: Congruent figure
Solve on a coordinate grid.
Question 6.
△ABC undergoes two transformations.
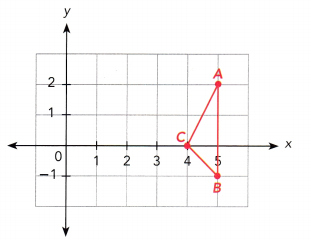
a) What would be the coordinates of △A”B”C” if △ABC is first translated 2 units up and 3 units left, and then reflected in the line x = 1?
Answer:
b) What would be the coordinates of △A”B”C” if △ABC is first reflected in the line x = 1, and then translated 2 units up and 3 units left?
Answer:
c) Do the two triangles △A”B”C” have the same coordinates? Are they congruent? Explain.
Answer:
Solve.
Question 7.
△PQR is mapped onto triangle △P’Q’R’ by using a transformation. △P”Q”R” is the image of △P’Q’R’ by using another transformation. Describe the sequence of transformations from △PQR to △P”Q”R”.
a)
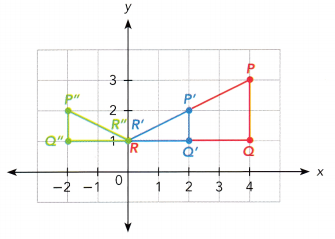
Answer: The above figure has dilation with center (0, 1) and scale factor of 0.5 and also we can see the reflection in the y-axis.
b)
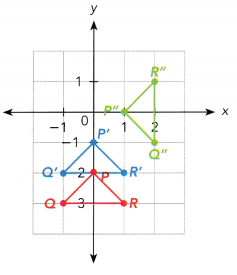
Answer: From the above figure we can see the translation of 1 unit up and then a rotation of 90 degrees counterclockwise about the origin.
c)
Answer: P’Q’R” is the reflection in the x-axis and P”Q”R” is the reflection in the y-axis.
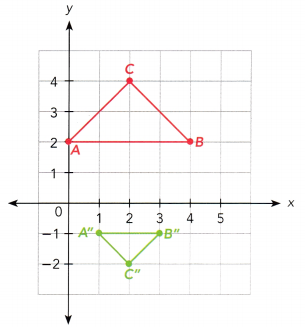
Question 8.
△ABC is mapped onto △A’B’C’, which is then mapped onto △A”B”C”. △ABC and △A”B”C” are shown in each diagram. Describe the sequence of transformations from △ABC to △A”B”C”. Then describe a single transformation from △ABC to △A”B”C”, if any.
a) △ABC is mapped onto △A’B’C’ by a rotation of 180° about (0, 0).
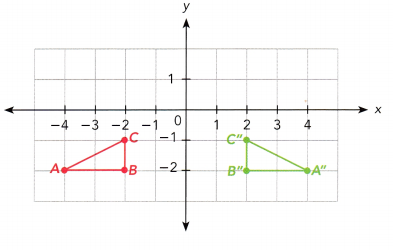
Answer:
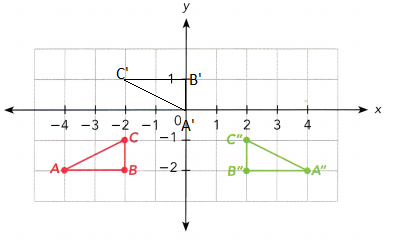
b) △ABC is mapped onto △A’B’C’ by a reflection in the line y = 1.
Answer:
Solve. Show your work.
Question 9.
Tom is at position A of a hall whose floor is a square with a bay of window across the front of the room. The length of the square is 30 meters. Describe how he gets to position C by a translation followed by a rotation about the center of the square.
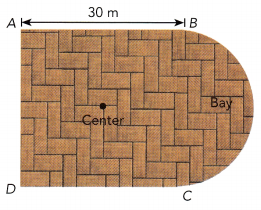
Answer:
Given,
Tom is at position A of a hall whose floor is a square with a bay of window across the front of the room.
The length of the square is 30 meters.
A translation of 30 meters forward followed by a rotation of 90 degrees clockwise direction about the center of the square.
Question 10.
The figure PQRST is dilated with center P and a scale factor 1.2. PQRST is mapped onto UVWXY. The area of PQRST is 24 square inches.
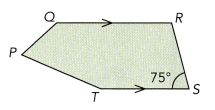
a) Find m∠WVX.
Answer: 75 degrees
b) Find the area of UVWXY.
Answer:
The area of PQRST is 24 square inches.
scale factor = 1.2
24 × 1.2 = 28.8 square inches.
Question 11.
Jack walks into a dark room. The area of the pupils of his eyes dilates to 3 times their normal area to allow more light into his eyes. By what scale factor is the diameter of his pupils enlarged?
Answer:
Given,
Jack walks into a dark room.
The area of the pupils of his eyes dilates to 3 times their normal area to allow more light into his eyes.
Diameter = √3 or 1.7321
Question 12.
Two similar cups are filled with water. The volume of water in the big cup is 80 cubic centimeters and the volume of water in the small cup is 10 cubic centimeters. If the height of the big cup is 8 centimeters, what is the height of the small cup?
Answer:
Given,
The volume of water in the big cup is 80 cubic centimeters and
the volume of water in the small cup is 10 cubic centimeters.
height of the big cup is 8 centimeters
Let the height of the small cup be x.
80/10 = 8/x
8 = 8/x
x = 8/8
x = 1
Therefore the height of the small cup is 1 cm.
Question 13.
Edward was blowing a circular bubble whose volume grew to 27 times its original size. It then drifted 8 units to the right and 11 units up before it burst.
a) Describe the sequence of transformations that the bubble went through.
Answer:
Given,
Edward was blowing a circular bubble whose volume grew to 27 times its original size.
It then drifted 8 units to the right and 11 units up before it burst.
V = 27 = 3³
So, the scale factor is 3
The sequence of transformations that the bubble went through is a dilation with the scale factor 3 and then a translation of 8 units to the right and 11 units up.
b) The original radius of the bubble was 2 centimeters. Find the final radius of the bubble.
Answer:
Given,
The original radius of the bubble was 2 centimeters.
Scale factor = 3
We know that
scale factor = scale/actual
3 = x/2
3 × 2 = x
x = 6 centimeters
Thus the final radius of the bubble is 6 centimeters.
Question 14.
An airplane at an airport terminal is cleared to take off by the control station after it moves from P to Q. The airplane’s path is marked by the thick arrows in the diagram. Describe the sequence of transformations that the airplane undergoes from P to Q.
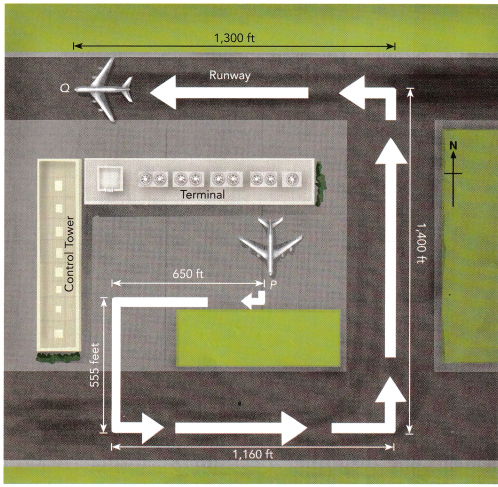
Answer:
Brain @ Work
Question 1.
A bridge is strung between two big trees on opposite sides of a river at P and Q. The bridge is to be removed and a new bridge is to be built across the river. The new bridge starts at P and spans the shortest distance across the river. Briefly describe how you would find the length of the new bridge using congruent triangles.
Answer:
Given data,
A bridge is strung between two big trees on opposite sides of a river at P and Q.
The bridge is to be removed and a new bridge is to be built across the river.
The new bridge starts at P and spans the shortest distance across the river.
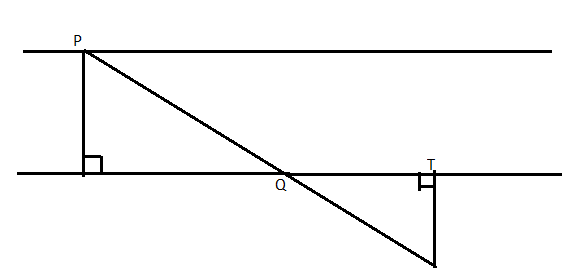
Draw a line from Q to R so that P, Q, R lie on the same straight line. Measure the distance TR such that it is perpendicular to the river bank. And TR is the length of new bridge using congruent triangles.
Question 2.
A souvenir in the shape of a rectangular prism is 20 centimeters by 15.5 centimeters by 13 centimeters. A pattern for a rectangular box, 29.2 centimeters by 18.6 centimeters by 16.9 centimeters, needs to be scaled down to fit the souvenir better. What is the minimum size of the box? Recommend a suitable set of measurements to the nearest 0.1 centimeter.
Answer: