Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 3 Review Test to finish your assignments.
Math in Focus Grade 6 Course 1 A Chapter 3 Review Test Answer Key
Concepts and Skills
Divide.
Question 1.
15 ÷ \(\frac{1}{3}\)
Answer: 45
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
\(\frac{15}{1}\) ÷ \(\frac{1}{3}\)
\(\frac{15}{1}\) x \(\frac{3}{1}\)
15 x 3 = 45
Question 2.
24 ÷ \(\frac{1}{6}\)
Answer: 144
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
24 ÷ \(\frac{1}{6}\)
24 x 6 = 144
Question 3.
\(\frac{3}{8}\) ÷ \(\frac{3}{4}\)
Answer:
\(\frac{1}{2}\)
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
\(\frac{3}{8}\) ÷ \(\frac{3}{4}\)
\(\frac{3}{8}\) x \(\frac{4}{3}\)
\(\frac{12}{24}\) = \(\frac{1}{2}\)
Question 4.
\(\frac{7}{12}\) ÷ \(\frac{1}{3}\)
Answer:
\(\frac{7}{3}\)Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
\(\frac{7}{12}\) ÷ \(\frac{1}{3}\)
\(\frac{7}{12}\) x \(\frac{3}{1}\)
\(\frac{21}{12}\) = \(\frac{7}{3}\)
Multiply.
Question 5.
0.3 × 8
Answer: 2.4
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
0.3 x 8 = 2.4
Question 6.
6 × 0.7
Answer: 4.2
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
6 x 0.7 = 4.2
Question 7.
0.28 × 6
Answer: 1.68
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
0.28 x 6 = 1.68
Question 8.
7 × 0.068
Answer: 0.476
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
7 x 0.068 = 0.476
Question 9.
0.3 × 0.6
Answer: 0.18
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
0.3 x 0.6 = 0.18
Question 10.
0.5 × 0.8
Answer: 0.4
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
0.5 x 0.8 = 0.4
Question 11.
5.7 × 0.4
Answer: 2.28
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
5.7 x 0.4 = 2.28
Question 12.
9.3 × 0.89
Answer: 8.277
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
9.3 x 0.89 = 8.277
Divide.
Question 13.
6 ÷ 0.6
Answer: 10
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.
6 ÷ 0.6 = 10

Question 14.
8 ÷ 0.4
Answer: 20
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.
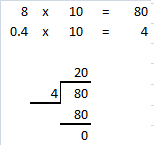
Question 15.
35 ÷ 0.7
Answer: 50
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.
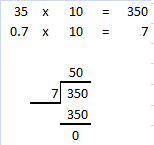
Question 16.
88 ÷ 0.2
Answer: 440
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.
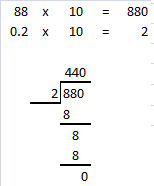
Question 17.
5 ÷ 0.25
Answer: 20
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.
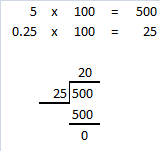
Question 18.
8 ÷ 0.16
Answer: 50
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.
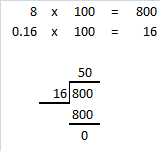
Question 19.
96 ÷ 0.16
Answer: 600
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.
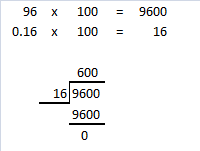
Question 20.
396 ÷ 0.36
Answer: 1,100
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.
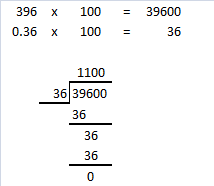
Question 21.
0.87 ÷ 0.03
Answer: 29
Explanation:
To divide a decimal number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.
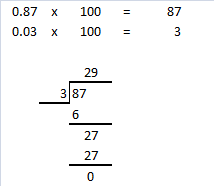
Question 22.
0.98 ÷ 0.7
Answer: 1.4
Explanation:
To divide a decimal number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.
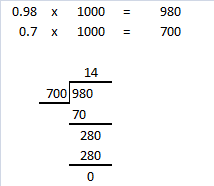
Problem Solving
Solve. Show your work.
Question 23.
In January, Jane volunteered at a hospital for a total of 12 hours. She spent \(\frac{4}{5}\) hour at the hospital every time she volunteered. How many times did Jane volunteer in January?
Answer:
15 times
Explanation:
In January, Jane volunteered at a hospital for a total of 12 hours.
She spent \(\frac{4}{5}\) hour at the hospital every time she volunteered.
Number times Jane volunteer in January
\(\frac{12}{1}\) ÷ \(\frac{4}{5}\)
\(\frac{12}{1}\) x \(\frac{5}{4}\)
3 x 5 = 15
Question 24.
Paul is making loaves of raisin bread to sell at a fundraising event. The recipe calls for \(\frac{1}{3}\) cup of raisins for each loaf, and Paul has 3\(\frac{1}{4}\) cups of raisins.
a) How many loaves can Paul make?
Answer:
Paul can make 9 loaves.
Explanation:
Paul has 3\(\frac{1}{4}\) cups of raisins.
The recipe calls for \(\frac{1}{3}\) cup of raisins for each loaf,
Number of loaves can Paul make are
\(\frac{13}{4}\) ÷ \(\frac{1}{3}\)
\(\frac{13}{4}\) x \(\frac{3}{1}\)
39 ÷ 4 = 9\(\frac{3}{4}\)
b) How many cups of raisins will he have left over?
Answer:
\(\frac{3}{4}\)
Explanation:
Paul has 3\(\frac{1}{4}\) cups of raisins.
The recipe calls for \(\frac{1}{3}\) cup of raisins for each loaf,
Number of loaves can Paul make are
\(\frac{13}{4}\) ÷ \(\frac{1}{3}\)
\(\frac{13}{4}\) x \(\frac{3}{1}\)
39 ÷ 4 = 9\(\frac{3}{4}\)
Number of loaves left over are \(\frac{3}{4}\)
Question 25.
Jane has a dog that eats 0.8 pound of dog food each day. She buys a 40-pound bag of dog food. How many days will this bag of dog food last?
Answer:
50 days
Explanation:
Jane has a dog that eats 0.8 pound of dog food each day.
She buys a 40-pound bag of dog food.
Number of days will this bag of dog food last
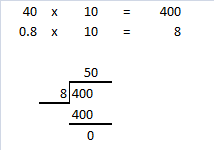
Question 26.
Mervin had some cartons of milk. He sold \(\frac{2}{5}\) of the cartons of milk in the morning. He then sold \(\frac{3}{4}\) of the remainder in the afternoon. 24 more cartons of milk were sold in the afternoon than in the morning. How many cartons of milk did Mervin have at first?
Answer:
480 cartons of milk.
Explanation:
total 5 parts
each part can be sub divided in to 4 parts each
in each box 24 cartons of milk
if total boxes are 20 and each box contains 24 cartons of milk
then the total number of milk is 24 x 20 = 480

Question 27.
Alice baked a certain number of pies. She gave \(\frac{1}{8}\) of the pies to her friends and \(\frac{1}{4}\) of the remainder to her neighbor. She was left with 63 pies. How many pies did Alice bake at first?
Answer:
96 pies
Explanation:
Let the original count of pies be represented by x
She gave \(\frac{1}{8}\) of the pies to her friend
So, x – \(\frac{1}{8}\)
A quarter of this given to the neighbor
x – \(\frac{x}{8}\) – x – \(\frac{x}{8}\) x \(\frac{1}{4}\) = 63
\(\frac{8x – x}{8}\) – \(\frac{8x – x}{8}\) x \(\frac{1}{4}\) = 63
\(\frac{7x}{8}\) – \(\frac{7x}{8}\) x \(\frac{1}{4}\) = 63
\(\frac{7x}{8}\) – \(\frac{7x}{32}\) = 63
\(\frac{7x}{32}\) – \(\frac{28x}{32}\) = 63
Multiply both sides by \(\frac{32}{21}\) x 63
x = 96
Question 28.
At a concert, \(\frac{2}{5}\) of the people were men. There were 3 times as many women as children. If there were 45 more men than children, how many people were there at the concert?
Answer:
180 people
Explanation:
Let people= p
men = \(\frac{2}{5}\)p
Let children = c
women = 3c
men = \(\frac{2}{5}\)p = c+45
people = men + women + children
= \(\frac{2}{5}\)p + 3c + c
= \(\frac{2}{5}\)p + 4c
= \(\frac{3}{5}\)p = 4c
\(\frac{2}{5}\)p = c + 45
Children = 27
people = 180
So, 180 people at the show.
women = 3c = 3 x 27 = 81
men = \(\frac{2}{5}\)p = c+45
= 72
Question 29.
\(\frac{3}{4}\) of the students in a school were girls and the rest were boys. \(\frac{2}{3}\) of the girls and \(\frac{1}{2}\) of the boys attended the school carnival. Find the total number of students in the school if 330 students did not attend the carnival.
Answer:
Total number of students 880
Explanation:
girls = 3boys,
since \(\frac{3}{4}\) = 3 x \(\frac{1}{4}\)
\(\frac{2}{3}\) girls + \(\frac{1}{2}\) boys attended
\(\frac{2}{3}\) x 3boys + \(\frac{1}{2}\) boys
= \(\frac{5}{2}\) boys attended
subtract that from the total (boys + girls) students:
boys + girls – \(\frac{5}{2}\) boys = 330
4b – \(\frac{5}{2}\) boys = 330
\(\frac{3}{2}\) boys = 330
boys = 220
so, girls = 3b
= 220 x 3 = 660
Boys + Girls = (220 + 660) = 880
There are 880 students
660 girls and 220 boys
440 girls and 110 boys attended = 550
the remaining 330 did not attend.
Question 30.
At a baseball game, there were three times as many males as females. \(\frac{5}{6}\) of the males were boys and the rest were men. \(\frac{2}{3}\) of the females were girls and the rest were women. Given that there were 121 more boys than girls, how many adults were there at the baseball game?
Answer:
55 adults
Explanation:
Number of females x
Number of girls = \(\frac{2}{3}\) x – girls
Number of women = \(\frac{1}{3}\) x
Number of males = 3x
Number of boys = \(\frac{5}{6}\) x 3x
= \(\frac{5}{2}\) x – boys
Number of men = \(\frac{1}{6}\) x 3x
= \(\frac{1}{2}\) x – men
So, \(\frac{5}{2}\) – 121 = \(\frac{2}{3}\) x
\(\frac{15}{6}\)x – \(\frac{4}{6}\)x = 121
\(\frac{11}{6}\)x = 121
x = 66
Men = \(\frac{1}{2}\) x 66 = 33
Women = \(\frac{1}{3}\) x 66 = 22
Adults = Men + Women
Adults = 33 + 22 = 55
Question 31.
Mr. Thomas spent $1,600 of his savings on a television set and \(\frac{2}{5}\) of the remainder on a refrigerator. He had \(\frac{1}{3}\) of his original amount of savings left.
a) What was Mr. Thomas’s original savings?
Answer:
$3600
b) What was the cost of the refrigerator?
Answer:
$2400
Explanation:
Let x is the savings,
x−(1600+(2x− \(\frac{1600}{5}\)) = x3
Because x is total amount of savings and he spent $1600
So, now he has 2÷5 of the total amount – $1600
(x÷3 Because he has 1÷3 of his original amount of savings)
x+(−1600−2x− \(\frac{3200}{5}\)) = x3
3x+3(−1600+−2x+ \(\frac{3200}{5}\))=x
3x+(−4800+−6x+ \(\frac{9600}{5}\))=x
3x+(−4800−1.2x+1920)=x
2x=4800+1.2x−1920.
8x=2880
x=3600
Question 32.
Sue buys 8.5 pounds of chicken to make tacos. She uses 0.3 pound of chicken for each taco.
a) How many tacos can Sue make?
Answer:
Sue can make 28 tacos
b) How many pounds of chicken are left over?
Answer:
\(\frac{1}{3}\) left over
Explanation:
Sue buys 8.5 pounds of chicken to make tacos.
She uses 0.3 pound of chicken for each taco.
\(\frac{8.5}{0.3}\)
= 28 \(\frac{1}{3}\)