Math in Focus Grade 6 Chapter 1 Lesson 1.5 Answer Key Cubes and Cube Roots

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 1 Lesson 1.5 Cubes and Cube Roots to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 1 Lesson 1.5 Answer Key Cubes and Cube Roots

Math in Focus Grade 6 Chapter 1 Lesson 1.5 Guided Practice Answer Key

Find a cube of a whole number.

a) A cube has edges 2 centimeters long. Find its volume.

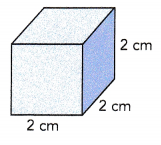
Volume of cube = 2 × 2 × 2 = 8 cm³
2 × 2 × 2 is called the cube of 2.
You can write 2 × 2 × 2 as 2³.
So, 2³ = 8.

The number 3 in 2³ is the exponent. The number 2 is the base.
The cube of a whole number is called a perfect cube.
Since 8 = 2 × 2 × 2, 8 is a perfect cube.

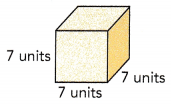
b) Find the cube of 7.
7³ = 7 × 7 × 7
= 343
The cube of 7 is 343.

I can relate this to finding the volume of a cube with edges of length 7 units.

Find the cube of each number.

Question 1.
5
Answer:
125

Explanation:
I can relate this to finding the volume of a cube with edges of length 5 units.
^{5³ = 5 x 5 x 5}
= 125
The cube of 5 is 125.

Question 2.
6
Answer:
216

Explanation:
I can relate this to finding the volume of a cube with edges of length 7 units.
^{7³ = 7 x 7 x 7}
= 216
The cube of 6 is 216.

Question 3.
9
Answer:
729

Explanation:
I can relate this to finding the volume of a cube with edges of length 9 units.
^{9³ = 9 x 9 x 9}
= 729
The cube of 5 is 729.

Find a cube root of a perfect cube.

a) A cube has a volume of 27 cubic meters. Find the length of each edge of the cube.

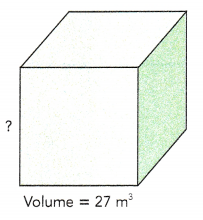
You know that
Volume of cube = edge × edge × edge.
To find the length of the edge of the cube, you need to find a number whose cube is 27.
You know that 3 × 3 × 3 = 27.
So, the length of each edge of the cube is 3 meters. 3 is called the cube root of 27. This can be written as
\(\sqrt[3]{27}\) = 3
Finding the cube root of a number is the inverse of finding the cube of a number.

b) Find the cube root of 64.
By prime factorization,

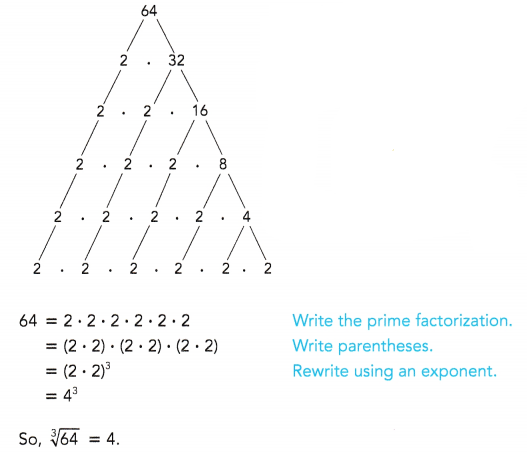
I can relate this to finding the length of an edge of a cube, when I know it has a volume of 64 units³.

Find the cube root of each number.

Question 4.
216
Answer:
6

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 216 = 2 x 2 x 2 x 3 x 3 x 3
= (2.3)³
=6³
so, cube root of 216 is 6.

Question 5.
343
Answer:
7

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 343 = 7 x 7 x 7
=7³
so, cube root of 343 is 7.

Question 6.
1,000
Answer:
10

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 1000 = 2 x 2 x 2 x 5 x 5 x 5
= (2.5)³
=10³
so, cube root of 1000 is 10.

Complete.

Question 7.
Find the values of 5² + 5³ and 5 • 5 • 5 • 5 • 5.

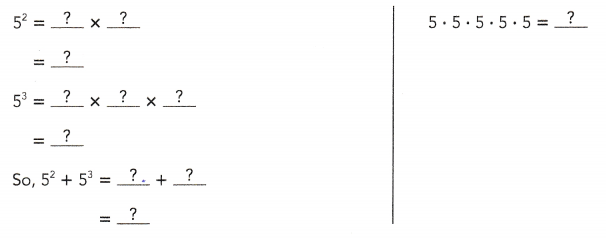
Answer:

Find the value of each of the following.

Question 8.
6³ + 4²
Answer:
232

Explanation:
6³ = 6 x 6 x 6= 216
4² = 4 x 4 = 16
6³ + 4² =  216 + 16 = 232
6³ + 4²  = 232

Question 9.
7³ – 4³
Answer:
279

Explanation:
7³ = 7 x 7 x 7 = 343
4³ = 4 x 4 x 4 = 64
7³ – 4³ = 343 – 64 = 279
7³ – 4³ = 279

Question 10.
3² × 5³ + 9²
Answer:
215

Explanation:
3² = 3 x 3 = 9
5³ = 5 x 5 x 5 = 125
9² = 9 x 9 = 81
3² x 5³ x 9² = 9+125+81 = 215.
3² x 5³ x 9²  = 215.

Question 11.
8³ ÷ 4² – 5²
Answer:
7

Explanation:
8³ = 8 x 8 x 8 = 512
4² = 4 x 4 = 16
5² = 5 x 5 = 25
8³ ÷ 4² – 5² = 512 ÷ 16 – (25)
= 32 – 25
= 7

8³ ÷ 4² – 5² = 7

Question 12.
7² + 6³ ÷ 2³
Answer:
76

Explanation:
7²  = 7 x 7 = 49
6³ = 6 x 6 x 6 = 216
2³ = 2 x 2 x 2 = 8
7² + 6³ ÷ 2³ = 49 + (216 ÷ 8)
= 49 + 27
= 76
7² + 6³ ÷ 2³ = 76

Question 13.
9³ – 4² × 3³
Answer:
297

Explanation:
9³ = 9 x 9 x 9 = 729
4² = 4 x 4 = 16
3³ = 3 x 3 x 3 = 27
9³ – 4² + 3³ = 729 – (16 x 27)
= 729 – 432
= 279
9³ – 4² + 3³ = 279.

Math in Focus Course 1A Practice 1.5 Answer Key

Find the cube of each number.

Question 1.
8
Answer:
512

Explanation:
I can relate this to finding the volume of a cube with edges of length 8 units.
^{8³ = 8 x 8 x 8}
= 64 x 8
= 512
The cube of 8 is 512.

Question 2.
3
Answer:
27

Explanation:
I can relate this to finding the volume of a cube with edges of length 3 units.
^{3³ = 3 x 3 x 3}
9 x 3
= 27
The cube of 3 is 27.

Question 3.
10
Answer:
1000

Explanation:
I can relate this to finding the volume of a cube with edges of length 10 units.
^{10³ = 10 x 10 x 10}
=100 x 10
= 1000
The cube of 10 is 1000.

Find the cube root of each number.

Question 4.
125
Answer:
5

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 125 = 5 x 5 x 5
=5³
so, cube root of 125 is 5.

Question 5.
512
Answer:
8

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 512 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
= (2.2.2)³
=8³
so, cube root of 512 is 8.

Question 6.
729
Answer:
9

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 729 = 3 x 3 x 3 x 3 x 3 x 3
= (3.3)³
=9³
so, cube root of 729 is 9.

Solve.

Question 7.
List the perfect cubes that are between 100 and 600.
Answer:
125, 216, 343 and 512.

Explanation:
125, 216, 343 and 512 are the perfect cubes between 100 and 600.

Question 8.
Math Journal Find the value of each expression. Then describe any patterns you see.
a) 2² – 1²
Answer:
3

Explanation:
2² = 2 x 2 = 4
1² = 1 x 1 = 1
2² – 1² = 4 – 1
= 3
2² – 1² = 3.

b) 3² – 2²
Answer:
5

Explanation:
3² = 3 x 3 = 9
2² = 2 x 2 = 4
3² – 2² = 9 – 4
= 5
3² – 2² = 5.

c) 4² – 3²
Answer:
7

Explanation:
4² = 4 x 4 = 16
3² = 3 x 3 = 9
4² – 3² = 16 – 9
= 7
4² – 3² = 7.

d) 5² – 4²
Answer:
9

Explanation:
5² = 5 x 5 = 25
4² = 4 x 4 = 16
5² – 4² = 25 – 16
= 9
5² – 4² = 9.

Question 9.
Find two consecutive numbers whose squares differ by 17.
Answer:
8 and 9

Explanation:
The square of 8 is 64
The square of 9 is 81
81 – 64 = 17
So, 8 and 9 are two consecutive numbers whose squares differ by 17.

Find the value of each of the following.

Question 10.
8³ + 5²
Answer:
537

Explanation:
8³ = 8 x 8 x 8 = 512
5² = 5 x 5 = 25
8³ + 5² = 512 + 25
= 537
8³ + 5² = 537.

Question 11.
10³ – 6²
Answer:
964

Explanation:
10³ = 10 x 10 x 10 = 1000
6² = 6 x 6 = 36
10³ – 6² = 1000 – 36
= 964
10³ – 6² = 964.

Question 12.
3³ × 9²
Answer:
2187

Explanation:
3³ = 3 x 3 x 3 = 27
9² = 9 x 9 = 81
3³ x 9² = 27 x 81
= 2187
3³ x 9² = 2187

Question 13.
9³ – 5² + 6²
Answer:
740

Explanation:
9³ = 9 x 9 x 9 = 729
5² = 5 x 5 = 25
6² = 6 x 6 = 36
9³ –  5² + 6² = 729 – 25 + 36
= 740
9³ – 5² + 6² = 740.

Question 14.
7² + 8³ – 4²
Answer:
545

Explanation:
7² = 7 x 7 = 49
8³ = 8 x 8 x 8 = 512
4² = 4 x 4 = 16
7² + 8³ – 4² = 49 + 512 – 16
= 545
7² + 8³ – 4² = 545

Question 15.
9³ – 5² + 6²
Answer:
740

Explanation:
9³ = 9 x 9 x 9 = 729
5² = 5 x 5 = 25
6² = 6 x 6 = 36
9³ – 5² + 6² = 729 – 25  + 36
= 740
9³ – 5² + 6² = 740

Question 16.
8³ × 5³ ÷ 5²
Answer:
2560

Explanation:
8³ = 8 x 8 x 8 = 512
5³ = 5 x 5 x 5 = 125
5² = 5 x 5 = 25
8³ × 5³ ÷ 5² = 512 x 125 ÷ 25
= 2560
8³ × 5³ ÷ 5² = 2560

Question 17.
10³ ÷ 8² × 4²
Answer:
250

Explanation:
10³ = 10 x 10 x 10 = 1000
8² = 8 x 8 = 64
4² = 4 x 4 = 16
10³ ÷ 8² x 4² = 1000 ÷ 64 x 16
= 250
10³ ÷ 8² x 4² = 250.

Question 18.
7³ – 10² ÷ 2²
Answer:
318

Explanation:
7³ = 7 x 7 x 7 = 343
10² = 10 x 10 = 100
2² = 2 x 2 = 4
7³ – 10² ÷ 2² = 343 – (100 ÷ 4 )
= 343 – 25
= 318
7³ – 10² ÷ 2² = 318

Question 19.
3³ + 4³ × 6²
Answer:
2331

Explanation:
3³ = 3 x 3 x 3= 27
4³ = 4 x 4 x 4 = 64
6² = 6 x 6 = 36
3³ + 4³ × 6² = 27 + (64 x 36 )
= 27 + 2304
= 2331
3³ + 4³ × 6² = 2331.

Find the value of each of the following.

Question 20.
17³
Answer:
4913

Explanation:
I can relate this to finding the volume of a cube with edges of length 17 units.
17³ = 17 x 17 x 17
= 289 x 17
= 4913
The cube of 17 is 4913.

Question 21.
16³
Answer:
4096

Explanation:
I can relate this to finding the volume of a cube with edges of length 16 units.
16³ = 16 x 16 x 16
= 256 x 16
= 4096
The cube of 16 is 4096.

Question 22.
18³
Answer:
5832

Explanation:
I can relate this to finding the volume of a cube with edges of length 18 units.
18³ = 18 x 18 x 18
= 324 x 18
= 5832
The cube of 18 is 5832.

Question 23.

Answer:
12

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 1728 = 2 x 2x 2 x 2 x 2 x 2 x 3 x 3 x 3
= (2.2.3)³
=12³
So, cube root of 1728 is 12.

Question 24.

Answer:
20

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 8000 = 2 x 2 x 2 x 2 x 2 x 2 x 5 x 5 x 5
= (2.2.5)³
=20³
So, cube root of 8000 is 20.

Question 25.

Answer:
15

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 3375 = 3 x 3 x 3 x 5 x 5 x 5
= (3.5)³
=15³
So, cube root of 3375 is 15.

Solve.

Question 26.
Given that 11³ = 1,331, find the cube of 110.
Answer:
1,331,000

Explanation:
If 11³ = 1,331 then 110³ will be 1,331,000.

Question 27.
Given that 14³ = 2,744, find the cube root of 2,744,000.
Answer:
140³

Explanation:
If 14³ = 2,744 then cube root of 2,744,000 is 140³.

Question 28.
Given that = 16, evaluate 160³.
Answer:
4,096,000

Explanation:
If cube root 4096 is 16 then 160³ will be 4,906,000.

Question 29.
Evaluate 13² + 20³ – 18².
Answer:
7845

Explanation:
13² = 13 x 13 = 169
20³ = 20 x 20 x 20 = 8000
18² = 18 x 18 = 324
13² + 20³ – 18² = 169 + 8000 – 324
= 7845
13² + 20³ – 18² = 7845.

Question 30.
Evaluate the cube root of 12³ × 5³ + 8³.
Answer:
68

Explanation:
Cube root of 12³ × 5³ + 8³ will be the number itself
So, 12 x 5 + 8 = 68 is cube root of 12³ × 5³ + 8³.

Question 31.
Find three consecutive numbers whose cubes have a sum of 2,241.
Answer:
8, 9, 10

Explanation:
8³ = 512
9³ = 729
10³ = 1000
512 + 729 + 1000 = 2241
So, the three consecutive numbers whose cubes have a sum of 2241 are 8, 9 and 10.

Question 32.
A cubic crate with an edge length of 16 feet will be used to contain cubic wooden boxes. Each wooden box has an edge length of 4 feet. How many wooden boxes can the crate contain?
Answer:
4 wooden boxes

Explanation:
A cubic crate with an edge length of 16 feet will be used to contain cubic wooden boxes.
Each wooden box has an edge length of 4 feet
4 x 4 = 16
S0, the wooden crate can contain 4 wooden boxes.

Brain @ Work

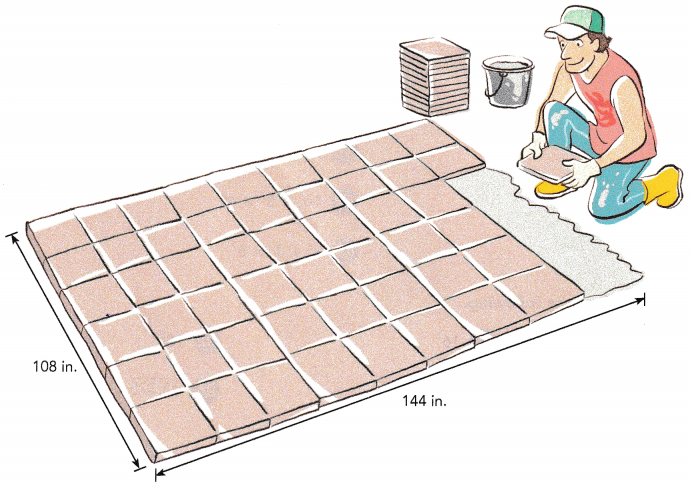
Mr. Henderson wants to tile his patio that is rectangular in shape. His patio measures 108 inches by 144 inches. Find the fewest square tiles he can use without cutting any of them. (Hint: First find the largest size tile he can use.)

Answer:
21 tiles of 12 inches square tile

Explanation:
Mr. Henderson wants to tile his patio that is rectangular in shape.
His patio measures 108 inches by 144 inches
The largest size tile he can use is 12 inches
12 in x 12 tiles = 144 in
12 in x 9 tiles = 108 in
So, Mr. Henderson wants 21 tiles of 12 inches to tile his patio in rectangular shape without cutting any square tile.