Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 7 Lesson 7.2 Constructing Perpendicular Bisectors to score better marks in the exam.
Math in Focus Grade 7 Course 2 B Chapter 7 Lesson 7.2 Answer Key Constructing Perpendicular Bisectors
Math in Focus Grade 7 Chapter 7 Lesson 7.2 Guided Practice Answer Key
Hands-On Activity
Materials:
- ruler
Explore The Distance Between Points On The Perpendicular Bisector Of A Segment And The Endpoints Of The Segment
Work in pairs.
Line XY is the perpendicular bisector of line segment AB. Points W, X, Y, and Z are four points on the perpendicular bisector of \(\overline{\mathrm{AB}}\).
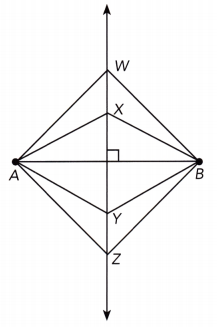
Measure and record each length to the nearest tenth of a centimeter.

Step 2.
Compare the lengths of \(\overline{A W}\) and \(\overline{B W}\). Then compare the lengths of each of the following pairs of segments: \(\overline{A X}\) and \(\overline{B X}\), \(\overline{A Y}\) and \(\overline{B Y}\), and \(\overline{A Z}\) and \(\overline{B Z}\). What do you notice about each pair of line segment lengths?
Answer:
Math Journal
Suppose you choose any point on the perpendicular bisector and measure the distances from that point to points A and B. What do you predict about the distances? What conclusion can you make?
From the activity, any point on the perpendicular bisector of a line segment is equidistant from the two endpoints of the line segment.

Complete.
Question 1.
Copy or trace triangle XYZ. Then draw the perpendicular bisector of line segment XY.
Answer:
Copy the triangle and complete.
Question 2.
A trucking company has most of its business in Cities P, Q, and R. Where should it locate its new facility so that it is equidistant from all three cities? Mark the location of the facility on a copy of the map.
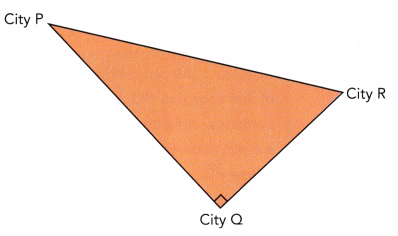
Answer:
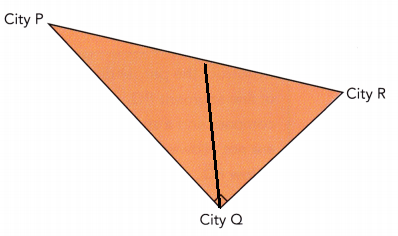
Math in Focus Course 2B Practice 7.2 Answer Key
Draw each line segment and construct its perpendicular bisector.
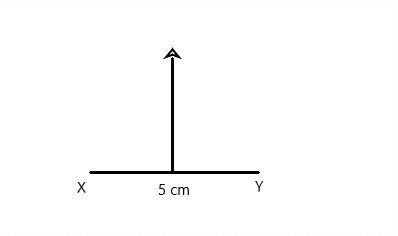
Question 1.
XY = 5 cm
Answer:
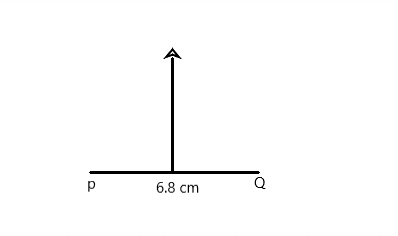
Question 2.
PQ = 6.8
Answer:
Question 3.
AB = 8.8 cm
Answer:
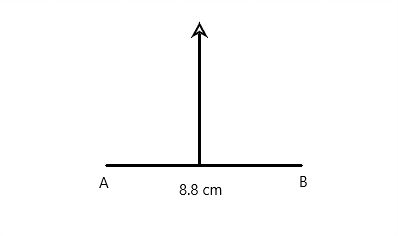
Question 4.
MN = 11 cm
Answer:
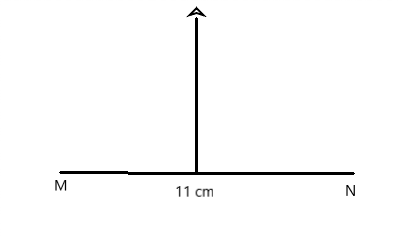
Question 5.
Draw a line segment between 4 inches and 5 inches and label the endpoints M and N. Construct the perpendicular bisector of \(\overline{\mathrm{MN}}\). Explain briefly if you could construct a different perpendicular bisector of \(\overline{\mathrm{MN}}\).
Answer:
Question 6.
Math Journal
In the diagram below, point M is the midpoint of \(\overline{\mathrm{AB}}\). Ben drew line segment XY through point M. He labeled it as the perpendicular bisector of \(\overline{\mathrm{AB}}\). Do you agree with Ben? Give a reason for your answer.
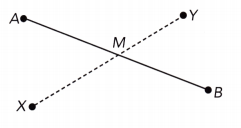
Answer:
Yes, I do agree with Ben.
Explanation:
In the given diagram, point M is the midpoint of \(\overline{\mathrm{AB}}\). Ben also drew line segment XY through point M. So Ben labeled it as the perpendicular bisector of \(\overline{\mathrm{AB}}\). A perpendicular bisector is a line that bisects another line at a right angle, through the intersection point. Hence I agree with Ben.
Question 7.
Answer:
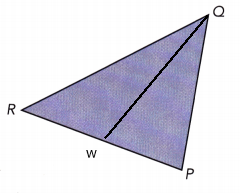
Question 8.
Draw the perpendicular bisectors of \(\overline{\mathrm{PQ}}\) and \(\overline{\mathrm{PR}}\) on a copy of each polygon. Label the point where the two perpendicular bisectors meet as W.
Answer:
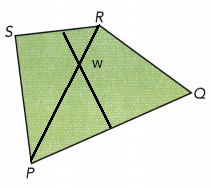
Question 9.
The point that is equidistant from points W, X, and Y. On a copy of WXYZ, mark the points that are described, if possible. Otherwise, explain why you cannot.
Answer:
We are given the polygon:
The point equidistant from points W, X and Y is the intersection of the perpendicular bisectors of the segments \(\overline{W X}\), \(\overline{X Y}\) and \(\overline{Y W}\).
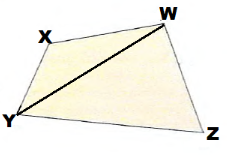
It is enough to draw two of the perpendicular bisectors as the three of them intersect in the same point.
We draw the perpendicuLar bisectors on \(\overline{X Y}\) and \(\overline{W X}\):
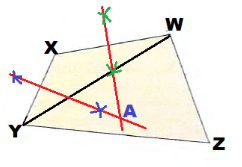
They intersect in point A. therefore A is the point that is equidistant from points W, X and Y.
Question 10.
The point that is equidistant from \(\overline{W X}\), \(\overline{W Z}\), and \(\overline{X Y}\).
Answer:
The points equidistant from \(\overline{W X}\) and \(\overline{W Z}\) are on the angle bisector of ∠XWZ.
The points equidistant from \(\overline{W X}\) and \(\overline{X Y}\) are on the angle bisector of ∠WXY.
Therefore the point equidistant from \(\overline{W X}\), \(\overline{W Z}\) and \(\overline{X Y}\) is the intersection of the two angle bisectors.
We draw the angle bisector of ∠XYZ:
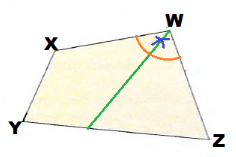
We draw the angle bisector of ∠WXY:
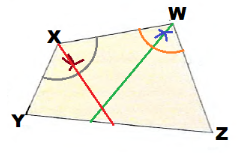
They intersect in point B, therefore B is the point that is equidistant from \(\overline{W X}\), \(\overline{W Z}\) and \(\overline{X Y}\):
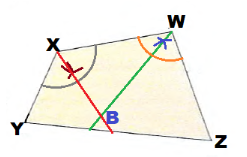
Question 11.
The point that is equidistant from \(\overline{W X}\) and \(\overline{W Z}\), and also from points X and Y.
Answer:
We are given the polygon:
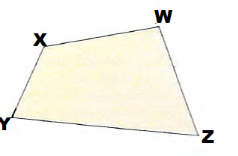
The points equidistant from \(\overline{W X}\) and \(\overline{W Z}\) are on the angle bisector of ∠XYZ.
The points equidistant from the points X and Y are on the perpendicular bisector of \(\overline{X Y}\).
Therefore the point equidistant from \(\overline{W X}\) and \(\overline{W Z}\) and from points X and Y is the intersection between the angle bisector of ∠XWZ and the perpendicular bisector of \(\overline{XY}\).
We draw the angle bisector of ∠XWZ:
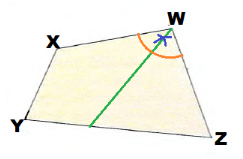
We draw the perpendicular bisector of \(\overline{XY}\):
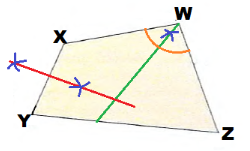
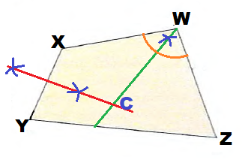
They intersect in point C, therefore C is the point that ¡s equidistant from \(\overline{W X}\) and \(\overline{W Z}\) and points X, Y.
Solve.
Question 12.
Mark the point on \(\overline{Q R}\) that is equidistant from points Q and R on a copy of triangle POR.
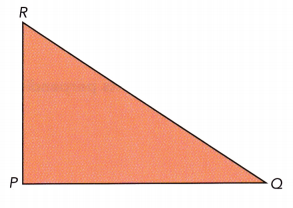
Answer:
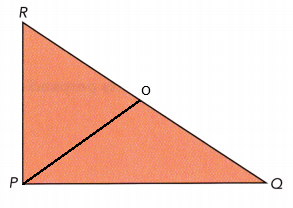
Question 13.
Mr. Smith wants to put a circular water sprinkler in his triangular-shaped garden. His garden has a tree at each vertex. The water sprinkler is to be equidistant from the trees. Copy or trace the given triangle. Mark point W to show where Mr. Smith should put the water sprinkler.
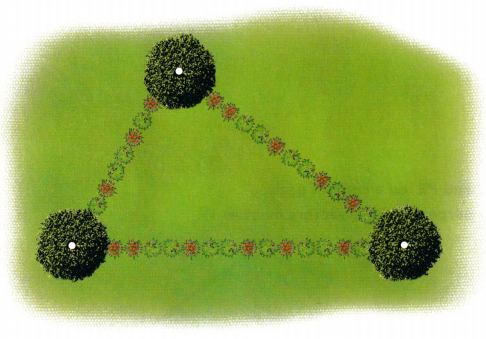
Answer:
We are given:

The point equidistant from the 3 trees is the intersection of the perpendicuLar bisectors of the triangles edges
It is enough to draw two of the perpendicular bisectors as the three of them intersect in the same point
We draw the perpendicular bisectors on two edges:
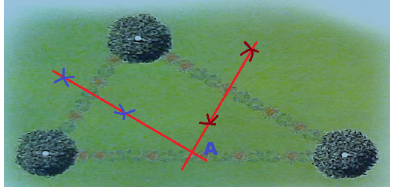
They intersect in point A. therefore A is the point that is equidistant from the 3 trees.
Question 14.
Math Journal
Melissa was asked to bisect a very long line segment using a compass and a straightedge. Melissa opened the compass to the widest possible setting. She found that it was not wide enough to do the standard construction that she had learned in math class. Is it possible for Melissa to bisect the very long line segment with only her compass and a straightedge? Explain and give a suggestion.
Answer:
Let \(\overline{A B}\) be the initial very long segment.
In order to be able to use an opening of the compass greater than half of a segment, she should ‘decrease the length of the given long segment as much as possible. For this, she places the compass, with its greatest opening, in point A and draw an arc which intersects \(\overline{A B}\) in X1. With the same opening she places the compass in B and draw an arc which intersects \(\overline{A B}\) in Y1.. She got a smaller segment \(\overline{X_{1} Y_{1}}\).
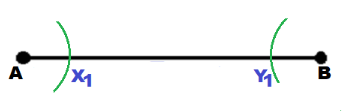
She continues placing the compass in X1 and Y1 and drawing arcs until she gets a segment \(\overline{X_{n} Y_{n}}\), for which she can construct the perpendicular bisector.
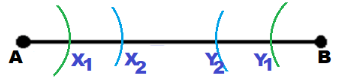
She constructs the perpendicular bisector of \(\overline{X_{n} Y_{n}}\), which is also the perpendicular bisector of \(\overline{A B}\) because AXn = BYn.
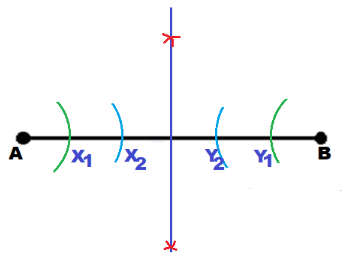
Decrease the length of the segment with equal values until the procedure of constructing the perpendicular bisector can be applied.
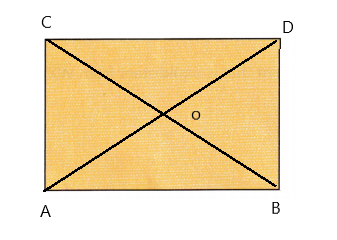
Question 15.
Math Journal
Copy the rectangle shown. Use the least possible number of arcs and lines to construct the perpendicular bisectors of each side of the rectangle. Explain how you know you have used the least possible number.

Answer: