Math in Focus Grade 7 Cumulative Review Chapters 3-5 Answer Key

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Cumulative Review Chapters 3-5 to score better marks in the exam.

Math in Focus Grade 7 Course 2 A Cumulative Review Chapters 3-5 Answer Key

Concepts and Skills

Simplify each expression. (Lessons 3.1, 3.2, 3.3)

Question 1.
3.9p + 0.9p – 1.8p
Answer:
3.9p + 0.9p – 1.8p
= 4.8p – 1.8p
= 3.0p

Question 2.
\(\frac{8}{3}\)x – \(\frac{3}{5}\)y + \(\frac{2}{5}\)x + \(\frac{7}{4}\)y
Answer:
\(\frac{8}{3}\)x – \(\frac{3}{5}\)y + \(\frac{2}{5}\)x + \(\frac{7}{4}\)y

= \(\frac{8}{3}\)x + \(\frac{2}{5}\)x + \(\frac{7}{4}\)y – \(\frac{3}{5}\)y

= \(\frac{(8 x 5) + (2 x 3)}{(3 x 5)}\)x + \(\frac{(7 x 5) – (3 x 4)}{(4 x 5)}\)y

= \(\frac{(40) + (6)}{15}\)x + \(\frac{(35) – (12)}{20}\)y

= \(\frac{46}{15}\)x + \(\frac{23}{20}\)y

Expand and simplify each expression. (Lesson 3.4)

Question 3.
-0.2(0.8q – 4)
Answer:
-0.2(0.8q – 4)
= (-0.2) x (0.8q) + (-0.2) x (-4)
= – 0.16q + 0.8

Question 4.
–\(\frac{2}{3}\)(-\(\frac{3}{4}\)y – \(\frac{1}{2}\))
Answer:
–\(\frac{2}{3}\)(-\(\frac{3}{4}\)y – \(\frac{1}{2}\))

= \(\frac{-2}{3}\)(\(\frac{-3}{4}\)y + \(\frac{-1}{2}\))

=(\(\frac{-2 X -3}{3 X 4}\)y) + (\(\frac{-2 X -1}{3 X 2}\))

=\(\frac{2}{4}\)y + \(\frac{1}{3}\)

=\(\frac{1}{2}\)y + \(\frac{1}{3}\)

Question 5.
5(\(\frac{1}{15}\)x – 6y) – \(\frac{1}{3}\)x
Answer:
5(\(\frac{1}{15}\)x – 6y) – \(\frac{1}{3}\)x

=\(\frac{5 X 1}{15}\)x – (5 X 6)y – \(\frac{1}{3}\)x

= \(\frac{5}{15}\)x – 30y – \(\frac{1}{3}\)x

= \(\frac{5}{5 X 3}\)x – 30y – \(\frac{1}{3}\)x

= \(\frac{1}{3}\)x – 30y – \(\frac{1}{3}\)x

= \(\frac{1}{3}\)x – \(\frac{1}{3}\)x – 30y

= -30y

Question 6.
2(m – n) – 6(n – 2m)
Answer:
2(m – n) – 6(n – 2m)
=2m – 2n -6n + 12m
=2m + 12m -2n-6n
=14m-8n

Write an algebraic expression for the shaded area shown in questions 7 and 8. Then expand and simplify the expression. (Lesson 3.4)

Question 7.

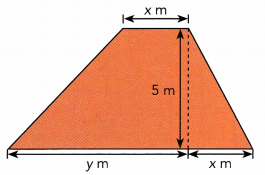
Answer:
Length = x in
Base = (y + x) in
Height = 5 m
Area of Trapezium = \(\frac{5}{2}\)(x + y + x) m²
\(\frac{5}{2}\)(x + y + x) m²
= \(\frac{5}{2}\)(2x + y) m² Add like terms
= \(\frac{5}{2}\)(2x) + \(\frac{5}{2}\)(y) m² Use Distributive Property
= (5x + \(\frac{5}{2}\)y)m² Multiply

Question 8.

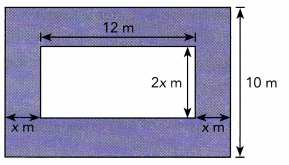
Answer:
Big Rectangle :
Length = 12 + x + x = (12 + 2x) m
width = 10 in
Area of Big Rectangle = Length × Width = (12 + 2x) ∙ (10)
= 12(10) + 2x(10) = (120 + 20x) m²
Small Rectangle :
Length = 12 m
Width = 2x m
Area of Small Rectangle = Length × Width = 12 ∙ 2x = 24x m²
Area of shaded area = (120 + 20x) – 24x m²
= (120 + 20x) – 24x
= 120 + 20x – 24x
= (120 – 4x) m²
Area = (120 + 20x — 24x) m² = (120 – 4x) m²

Factor each expression. (Lesson 3.5)

Question 9.
-4k – 36
Answer:
-4k – 36
= (-4)k + (-4)(9)
= -4(k + 9)

Question 10.
9 + 15m – 21n
Answer:
9 + 15m – 21n
=(3)(3) + (3)(5)m – (3)(7)n
= 3(3 + 5m – 7n)

Translate each verbal description into an algebraic expression. Simplify the expression when you can. (Lesson 3.6)

Question 11.
50% of one-twentieth of the product of 12 and 5z + 5.
Answer:
50% of one-twentieth of the product of 12 and 5z + 5

=(50%) X (\(\frac{1}{20}\)) X (12) X (5z + 5)

= (\(\frac{50}{100}\)) X (\(\frac{1}{20}\)) X (12) X (5z + 5)

= (\(\frac{1}{2}\)) X (\(\frac{1}{20}\)) X (12) X (5z + 5)

= (\(\frac{1 X 1 X 12}{2 X 20}\)) X (5z + 5)

= (\(\frac{12}{40}\)) X (5z + 5)

= (\(\frac{12}{40}\)) X (5z + 5)

= (\(\frac{3}{10}\)) X (5z + 5)

= (\(\frac{3}{10}\)) X (5)(z + 1)

=(\(\frac{3 X 5}{10}\)) X (z + 1)

=(\(\frac{3}{2}\)) X (z + 1)

=\(\frac{3}{2}\)z +\(\frac{3}{2}\)

 

Question 12.
21 plus 6p minus two-thirds the sum of 14p and 3q.
Answer:
21 plus 6p minus two-thirds the sum of 14p and 3q
= 21 + 6p – \(\frac{2}{3}\)(14p + 3q)

= 21 + 6p – \(\frac{2 X 14p}{3}\) – \(\frac{2 X 3q}{3}\)

= 21 + 6p – \(\frac{2 X 14p}{3}\) – \(\frac{2 X 3q}{3}\)

= 21 + 6p – \(\frac{28p}{3}\) – 2q

= 21 + \(\frac{3 X 6p}{3}\) – \(\frac{28p}{3}\) – 2q

= 21 + \(\frac{18p}{3}\) – \(\frac{28p}{3}\) – 2q

= 21 + \(\frac{18p-28p}{3}\)– 2q

= 21 + \(\frac{-10p}{3}\)– 2q

= 21 – \(\frac{10}{3}\)p- 2q

Tell whether each pair of equations are equivalent. (Lesson 4.1)

Question 13.
x – 7 = 1 and x = 6
Answer:
The above equations are not equivalent
If x = 6, and if we substitute it in
x – 7 = 1
(6) – 7 = 1
-1 = 1  -> False

Hence they are not equivalent.

Question 14.
0.2x = 0.6 and 3x + 1 =10
Answer:
The above equations are equivalent.
Equation 1
0.2x = 0.6
2x = 6
x = 3

Equation 2
3x + 1 = 10
3(3) + 1 = 10
9 + 1 = 10
10 = 10  -> True

Hence they are equivalent.

Solve each equation. (Lesson 4.2)

Question 15.
11 + 4k = 7
Answer:
11 + 4k = 7
4k = 7 – 11
4k = -4
k = -1

Question 16.
5p + \(\frac{2}{15}\) = \(\frac{3}{5}\) + \(\frac{4}{5}\)p
Answer:

5p + \(\frac{2}{15}\) = \(\frac{3}{5}\) + \(\frac{4}{5}\)p

5p – \(\frac{4}{5}\)p = \(\frac{3}{5}\) – \(\frac{2}{15}\)

\(\frac{5 X 5}{5}\)p – \(\frac{4}{5}\)p = \(\frac{3 X 3}{5 X 3}\) – \(\frac{2}{15}\)

\(\frac{25}{5}\)p – \(\frac{4}{5}\)p = \(\frac{9}{15}\) – \(\frac{2}{15}\)

\(\frac{21}{5}\)p = \(\frac{7}{15}\)

\(\frac{7 X 3}{5}\)p = \(\frac{7}{5 X 3}\)

\(\frac{3}{1}\)p = \(\frac{1}{3}\)

3p = \(\frac{1}{3}\)

p = \(\frac{1}{3 X 3}\)

p = \(\frac{1}{9}\)

Question 17.
\(\frac{8}{9}\)(4x – 3) = \(\frac{2}{3}\)
Answer:
\(\frac{8}{9}\)(4x – 3) = \(\frac{2}{3}\)

\(\frac{4 X 2}{3 X 3}\)(4x – 3) = \(\frac{2}{3}\)

\(\frac{4}{3}\)(4x – 3) = \(\frac{2 X 3}{3 X 2}\)

\(\frac{4}{3}\)(4x – 3) = \(\frac{1}{1}\)

\(\frac{4}{3}\)(4x – 3) = 1

4(4x – 3) = 3
(4)(4x) – (4)(3) = 3
16x – 12 = 3
16x = 3 + 12
16x = 15

x = \(\frac{15}{16}\)

Question 18.
7(x + 5) – 3x = x – 7
Answer:
7(x + 5) – 3x = x – 7
7x + 35 – 3x = x – 7
7x  – 3x – x = – 7 – 35
7x – 4x = -42
3x = – 42
x = -14

 

Solve each inequality. Then graph each solution set on a number line. (Lesson 4.4)

Question 19.
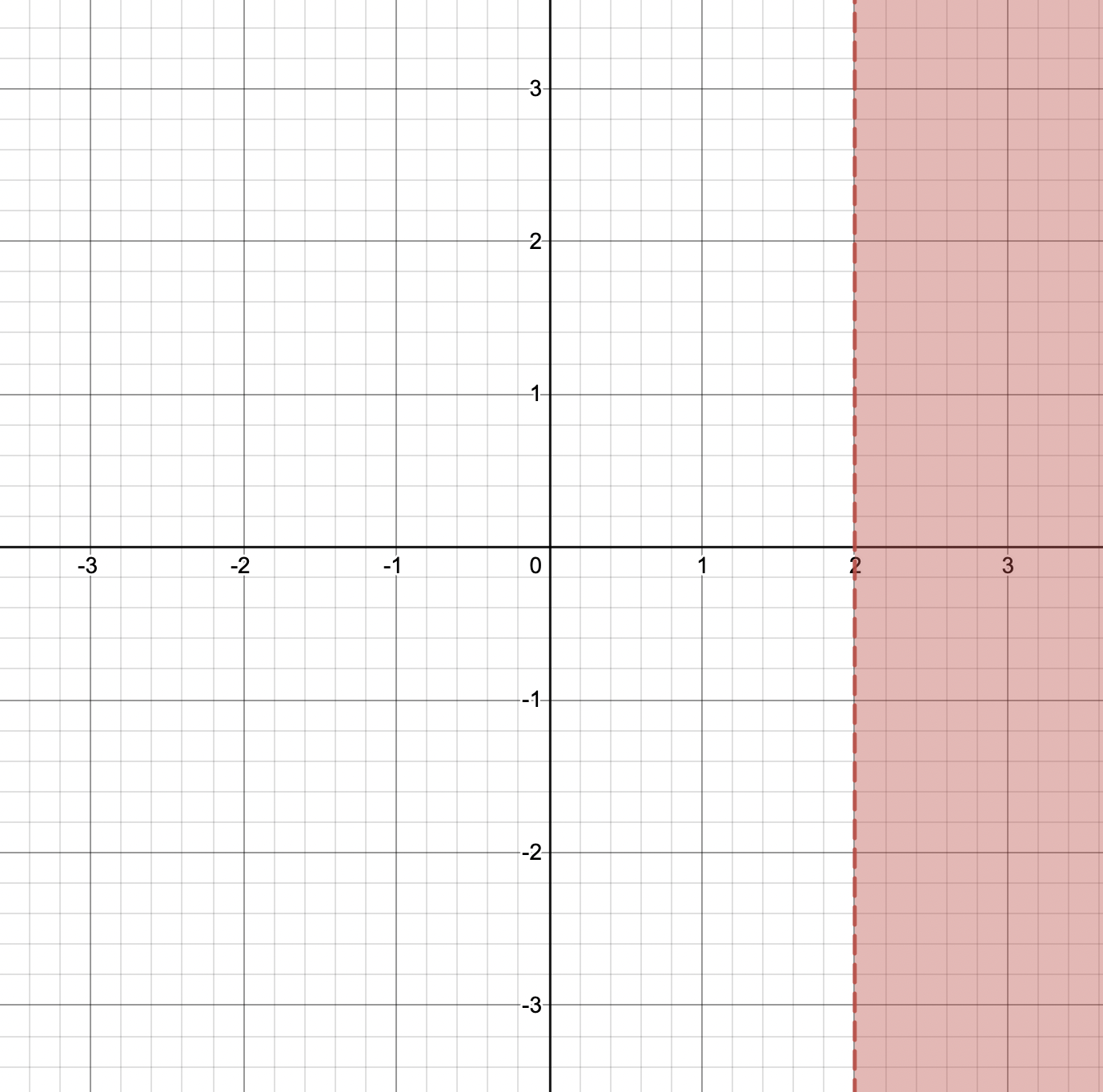
8x – 7 > 9
Answer:
8x – 7 > 9
8x > 9 + 7
8x > 16
x > 2

Question 20.
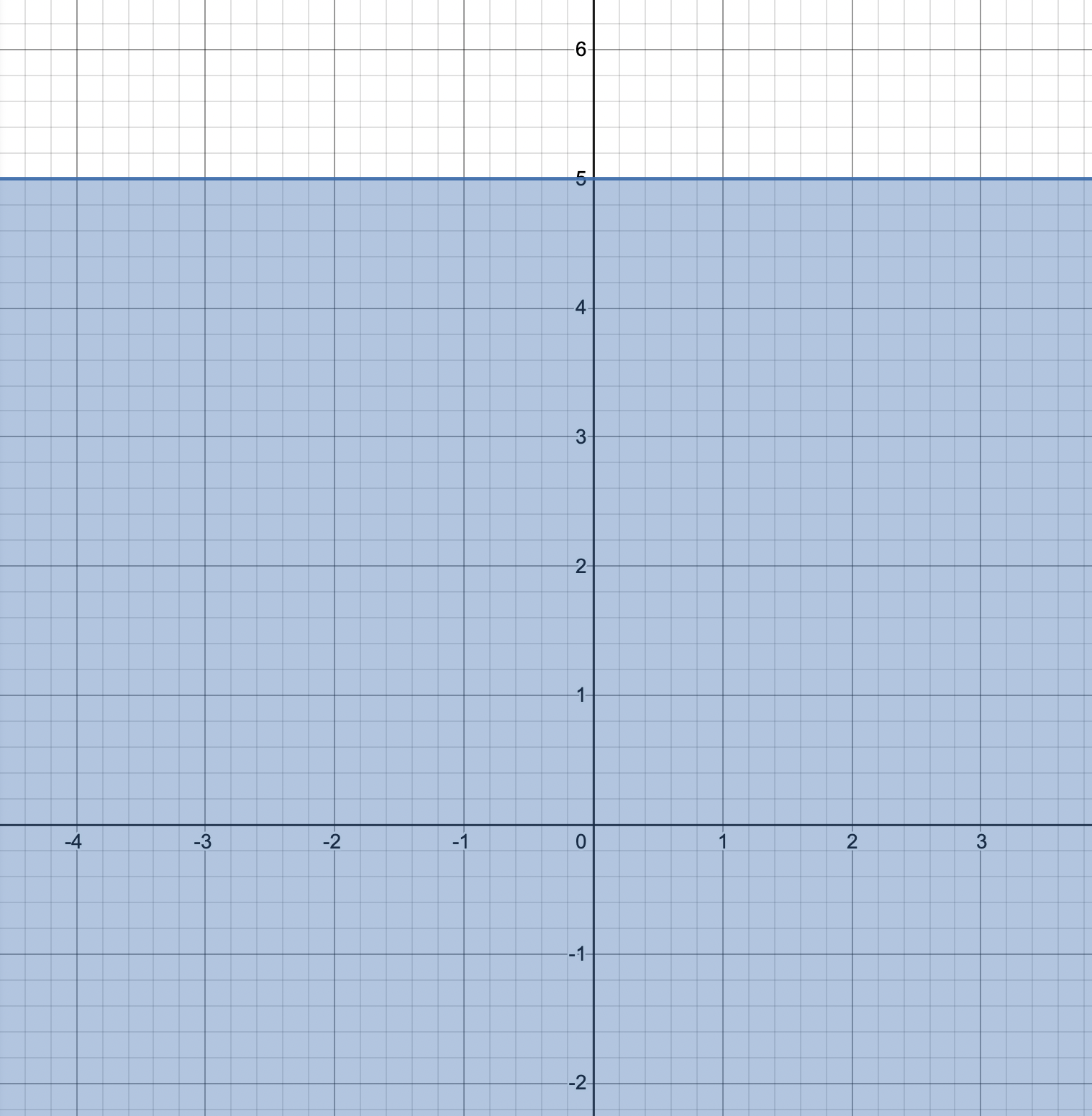
6 + \(\frac{2}{5}\)y ≤ \(\frac{1}{3}\)y + 6\(\frac{1}{3}\)
Answer:

6 + \(\frac{2}{5}\)y ≤ \(\frac{1}{3}\)y + 6\(\frac{1}{3}\)

\(\frac{2}{5}\)y – \(\frac{1}{3}\)y ≤ 6\(\frac{1}{3}\) – 6

\(\frac{2}{5}\)y – \(\frac{1}{3}\)y ≤ \(\frac{1}{3}\)

\(\frac{2 X 3}{5 X 3}\)y – \(\frac{1 X 5}{3 X 5}\)y ≤ \(\frac{1}{3}\)

\(\frac{6}{15}\)y – \(\frac{5}{15}\)y ≤ \(\frac{1}{3}\)

\(\frac{1}{15}\)y ≤ \(\frac{1}{3}\)

y ≤ \(\frac{15}{3}\)

y ≤ \(\frac{5 X 3}{3}\)

y ≤ 5

Question 21.
1.8(x – 5) ≥ 0.2(x – 13)
Answer:
1.8(x – 5) ≥ 0.2(x – 13)
(10)(1.8)(x – 5) ≥ (10)(0.2)(x – 13)
18(x – 5) ≥ 2(x – 13)
9(x – 5) ≥ 1(x – 13)
9x – 45 ≥ x – 13
9x – x ≥ -13 + 45
8x ≥ 32
x ≥ 4

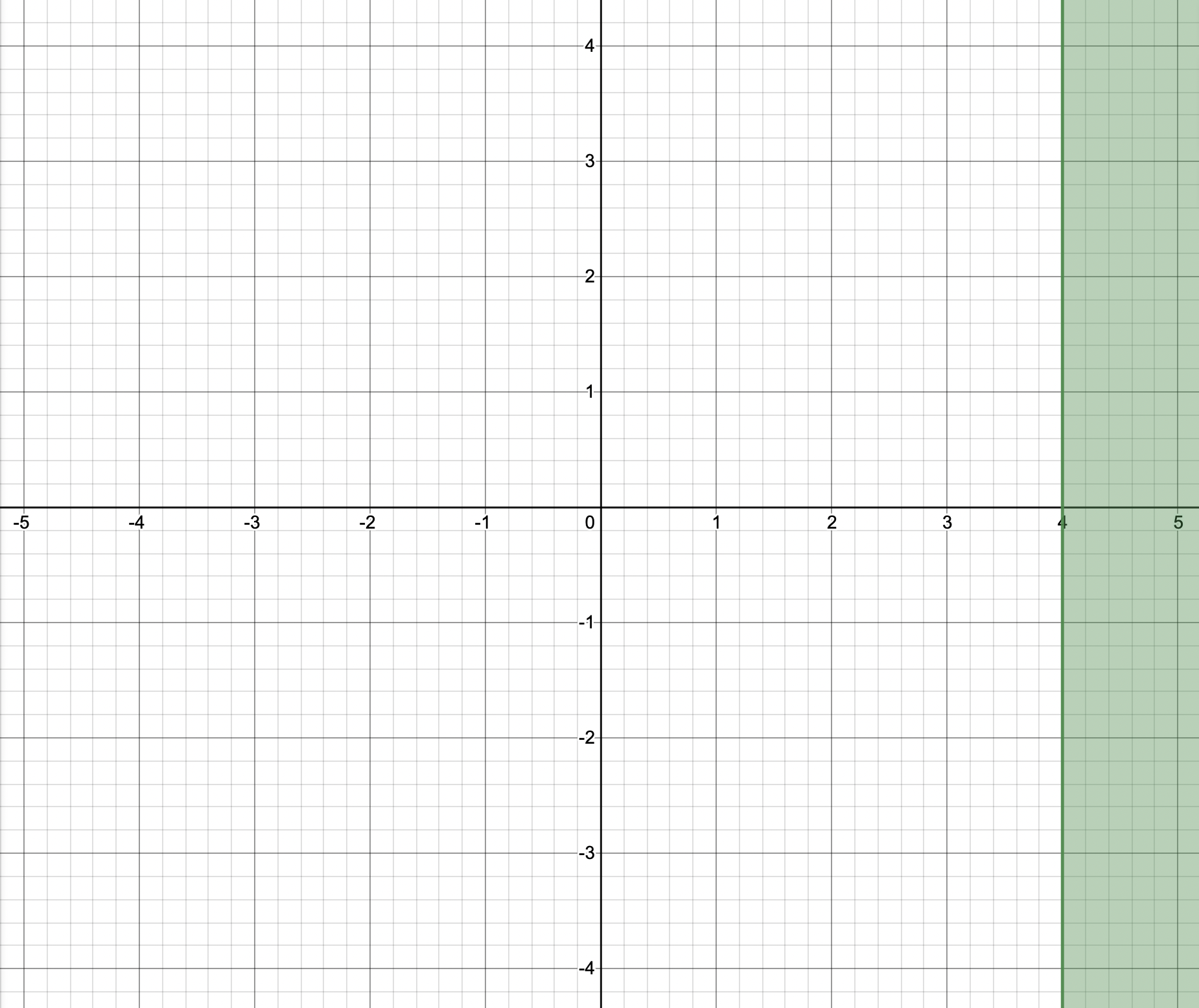
Question 22.
2(3 – r) + 4(1 + 3r) > – 2(3 – 7r)
Answer:
2(3 — r) + 4(1 + 3r) > —2(3 — 7r)
2(3) + 2(—r) + 4(1) + 4(3r) > —2(3) + (—2)(—7r) Use Distributive Property
6 — 2r + 4 + 12r > —6 + 14r Multiply
10r + 10 > —6 + 14r Combine like terms
10r + 10 — 10 > —6 + 14r — 10 Subtract 10 from both sides
10r > -16 + 14r Simplify
10r – 14r > -16 + 14r – 14r Subtract 14r from both sides
-4r > -16 Simplify
-4r > -16
\(\frac{-4}{-4} r\) > \(\frac{-16}{-4}\) Divide both sides by -4 and reverse sign of inequality
r < 4

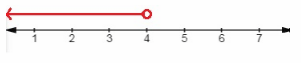
Use shaded circle for ≥ or ≤ and empty circle for < or >
The number line for r < 4 is shown

Tell whether each table, equation, or graph represents a direct proportion, an inverse proportion, or neither. Find the constant of proportionality for the direct and inverse proportion identified. (Lessons 5.1, 5.2, 5.4)

Question 23.

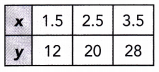
Answer:

Direct Proportion :
For each pair of values x and y →
\(\frac{y}{x}\) = \(\frac{12}{1.5}\) = 8
\(\frac{y}{x}\) = \(\frac{20}{2.5}\) = 8
\(\frac{y}{x}\) = \(\frac{28}{3.5}\) = 8
\(\frac{y}{x}\) is a constant so x and y is direct proportional
Inverse proportion :
For each pair of values x and y →
xy = 1.5 ∙ 12 = 18
xy = 2.5 ∙ 20 = 50
xy = 3.5 ∙ 28 = 98
xy is not a constant so y is not inversely proportional to x
NOTE:
Direct proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in Inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Direct Proportion

Question 24.

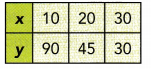
Answer:

Direct Proportion :
For each pair of values x and y →
\(\frac{y}{x}\) = \(\frac{90}{10}\) = 9
\(\frac{y}{x}\) = \(\frac{45}{20}\) = 2.25
\(\frac{y}{x}\) = \(\frac{30}{30}\) = 1
\(\frac{y}{x}\) is not a constant so x and y is not direct proportional

Inverse Proportion :
For each pair of values x and y →
xy = 10 ∙ 90 = 900
xy = 20 ∙ 45 = 900
xy = 30 ∙ 30 = 900
xy is a constant so y is inversely proportional to x

NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Inverse proportion

Question 25.

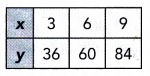
Answer:

Direct Proportion :
For each pair of valtes x and y →
\(\frac{y}{x}\) = \(\frac{36}{3}\) = 12
\(\frac{y}{x}\) = \(\frac{60}{6}\) = 10
\(\frac{y}{x}\) = \(\frac{84}{9}\) = 9.33
\(\frac{y}{x}\) is not a constant so x and y is not direct proportional

Inverse Proportion :
For each pair of values x and y →
xy = 3 ∙ 36 = 108
xy = 6 ∙ 60 = 360
xy = 9 ∙ 84 = 756
xy is not a constant so y is not inversely proportzonal to x

NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Neither

Question 26.
y = 1.8x + 3.6
Answer:
y = 1.8x + 3.6
Direct proportion :
y = 1.8x + 3.6
Because the original equation y = 1.8x + 3.6 cannot be rewritten as an equivalent equation in the form y = kx, it does not represent a direct proportion.

Inverse Proportion :
y = 1.8x + 3.6
Because the original equation y = 1.8x + 3.6 cannot be rewritten as an equivalent equation in the form xy = k, it does not represent an inverse proportion.

NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Neither Direct Proportion nor Inverse Proportion

Question 27.
\(\frac{2}{5}\)y = \(\frac{1}{2}\)x
Answer:
\(\frac{2}{5}\)y = \(\frac{1}{2}\)x

Direct proportion :
\(\frac{2}{5}\)y = \(\frac{1}{2}\)
\(\frac{5}{2}\) ∙ \(\frac{2}{5}\)y = \(\frac{5}{2}\) ∙ \(\frac{1}{2}\)x Multiply both sides by \(\frac{5}{2}\)
y = \(\frac{5}{4}\)x
Because the original equation \(\frac{2}{5}\)y = \(\frac{1}{2}\)x can be rewritten as an equivalent equation in the form y = kx, it represent a direct proportion.

Inverse Proportion :
\(\frac{2}{5}\)y = \(\frac{1}{2}\)x
\(\frac{5}{2}\) ∙ \(\frac{2}{5}\)y = \(\frac{5}{2}\) ∙ \(\frac{1}{2}\)x Multiply both sides by \(\frac{5}{2}\)y

Because the original equation \(\frac{2}{5}\)y = \(\frac{1}{2}\)x cannot be rewritten as an equivalent equation in the form xy = k, it does not represent an inverse proportion.

NOTE:
Direct Proportion : y ‘is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as y = k or y = \(\frac{k}{x}\)
Direct proportion

Question 28.
3y = \(\frac{18}{x}\)
Answer:
3y = \(\frac{18}{x}\)
Direct Proportion :
3y = \(\frac{18}{x}\)
\(\frac{x}{3}\) ∙ 3y = \(\frac{x}{3}\) ∙ \(\frac{18}{3}\) Multiply both sides by \(\frac{x}{3}\)
Because the original equation 3y = \(\frac{18}{3}\) cannot be rewritten as an eqnivalent equation in the form y = kx, it does not represent a direct proportion.

Inverse Proportion :
3y = \(\frac{18}{3}\)
\(\frac{x}{3}\) ∙ 3y = \(\frac{x}{3}\) ∙ \(\frac{18}{3}\) Multiply both sides by \(\frac{x}{3}\)
xy = 6
18
Because the original eqtiation 3y = \(\frac{18}{x}\) can be rewritten as an equivalent equation in the form xy = k, il represent an inverse proportion.

NOTE :
Direct Proportion : y is directly proportional to z then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant
of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Inverse Proportion

Question 29.

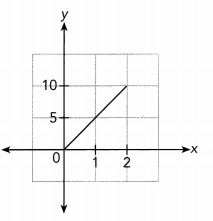
Answer:
Direct Proportion :
$From\ the\ graph$
\(\frac{y}{x}\) = \(\frac{5}{1}\) = 5
\(\frac{y}{x}\) = \(\frac{10}{2}\) = 5
\(\frac{y}{x}\) = Constant
The given graph is a straight line that does not lie along the x — axis or y — axis and does pass through the origin.
So, the given graph represents a direct proportion.
Inverse Proportion :
$Use\graph\: $
x ∙ y = 1 ∙ 5 = 5
x ∙ y = 2 ∙ 10 = 20
The product of x and y is not a constant so x and y does not represent an inverse proportion.
Direct proportion

Question 30.

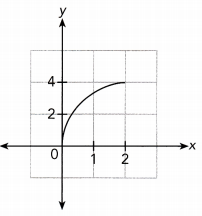
Answer:

Question 31.

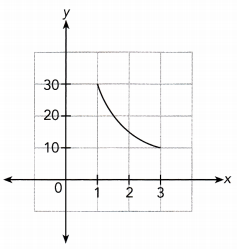
Answer:
Direct Proportion:
The given graph is not a straight tine that does tie along the x — axis and don not pass through the origin.
So, the given graph does not represents a direct proportion.

Inverse Proportion:
Use graph
x ∙ y = 1 ∙ 30 = 30
x ∙ y = 3 ∙ 10 = 30
The product of x and y is a constant so x and y represent an inverse proportion.
Inverse Proportion

In each table, y is directly proportional to x. Find the constant of proportionality and then complete the table. (Lesson 5.3)

Question 32.

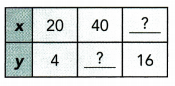
Answer:

Find Constant of Proportionality :
y is directly proportional to x :
\(\frac{y}{x}\) = \(\frac{4}{20}\)
\(\frac{y}{x}\) = \(\frac{1}{5}\) simplify
Constant of proportionality = \(\frac{1}{5}\)

Find Missing numbers :
Find y when x = 40
\(\frac{y}{x}\) = \(\frac{1}{5}\)
\(\frac{y}{40}\) = \(\frac{1}{5}\) Multiply both sides by 40
40 ∙ \(\frac{y}{40}\) = 40 ∙ \(\frac{y}{40}\)
y = 8
Find x when y = 16
\(\frac{y}{x}\) = \(\frac{1}{5}\)
\(\frac{16}{x}\) = \(\frac{1}{5}\) Evaluate y = 16
5 ∙ 16 = x ∙ 1 Cross Muttipliction
x = 80

Constant of proportionality = \(\frac{1}{5}\)
The missing number are 8 and 80 respectively

Question 33.

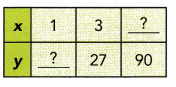
Answer:

y is directly proportional lo x :
\(\frac{y}{x}\) = \(\frac{27}{3}\)
\(\frac{y}{x}\) = 9 simplify
Constant of Proportionality = 9
Find Missing Numbers :
Find y when x = 1
\(\frac{y}{x}\) = 9
\(\frac{y}{1}\) = 9 Evaluate x = 1
y = 9
Find x when y = 90
\(\frac{y}{x}\) = 9
\(\frac{90}{x}\) = 9 Evaluate y = 90
\(\frac{x}{90}\) ∙ \(\frac{90}{x}\) = \(\frac{x}{9}\) ∙ 9 Multiply both sides by \(\frac{x}{9}\)
x = 10

Constant of Proportionality = 9
The missing numbers are 9 and 10 respectively

In each table, y is inversely proportional to x. Find the constant of proportionality and then complete the table. (Lesson 5.4)

Question 34.

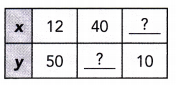
Answer:

Find Constant of Proportionality
y is Inversely proportional to x:
xy = 12 • 50
xy = 600 Slmplif y
Find missing value in tite table.
when x = 40 find y.
xy = 600
40 • y = 600 Evaluate x = 40
\(\frac{40 y}{40}\) = \(\frac{600}{40}\) Divide both sides by 4
y = 15 Simplify
when y = 10 find x,
x ∙ 10 = 600 Evaluate y = 10
\(\frac{10 x}{10}\) = \(\frac{600}{10}\) Divide both sides by 10
x = 60 Simplify

Constant of Proportionality = 600
The missing number are y = 15 and x = 60

Question 35.

Answer:

Find Constant of Proportionality
y is inversely proportional to x:
xy = 2 ∙ 4.5
xy = 9 Simplify
Find missing value in the table.
When x = 1 find y,
xy = 9
1 ∙ y = 9 Evaluate x = 1
y = 9 Simplify
When y = 3 find x,
x ∙ 3 = 9 Evaltate y = 3
\(\frac{3 x}{3}\) = \(\frac{9}{3}\) Divide both sides by 3
x = 3 Simplify

Constant of Proportionality = 9
The missing number are y = 9 and x = 3

Solve using proportional reasoning. (Lessons 5.3, 5.4)

Question 36.
y varies directly as x, and y = 4.8 when x = 0.2. Find y when x = 0.8.
Answer:
y = 4.8 and x = 0.2
y is directly proportional to x :
\(\frac{y}{x}\) = \(\frac{4.8}{0.2}\)
\(\frac{y}{x}\) = 24
x ∙ \(\frac{y}{x}\) = 24 ∙ x Multiply both sides by x
y = 24x
Find the value of y when x = 0.8
We know y = 24x,
y = 24 ∙ 0.8 Substituting x = 0.8
y = 19.2 Simplify

Question 37.
P is inversely proportional to Q, and P = \(\frac{1}{4}\) when Q = \(\frac{1}{2}\). Find P when Q = 2 \(\frac{1}{2}\).
Answer:
P = \(\frac{1}{4}\) and Q = \(\frac{1}{2}\)
Write an inverse proportion equation :
P is inversely proportional to Q :
P ∙ Q = \(\frac{1}{4}\) ∙ \(\frac{1}{2}\)
PQ = \(\frac{1}{8}\)

Find the value of P when Q = 2\(\frac{1}{2}\)
PQ = \(\frac{1}{8}\)
P ∙ 2\(\frac{1}{2}\) = \(\frac{1}{8}\) Substituting Q = 2\(\frac{1}{2}\)
\(\frac{5}{2}\)P = \(\frac{1}{8}\) Simplifying
\(\frac{2}{5}\) ∙ \(\frac{5}{2}\)P = \(\frac{1}{8}\) ∙ \(\frac{2}{5}\) Multiplying both sides by \(\frac{2}{5}\)
P = \(\frac{1}{20}\)

Problem Solving

Solve. Show your work.

Question 38.
The table shows the relationship between the capacity in quarts, x, and the capacity in cups, y. Graph the relationship between y and x. Use 1 unit on the horizontal axis to represent 1 quart and 1 unit on the vertical axis to represent 4 cups. (Chapter 5)

Answer:


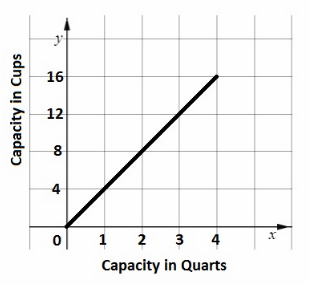
a) Is the number of cups directly proportional to the number of quarts? If so, find the constant of proportionality.
Answer:
The graph is a straight line through the origin, and It does not lie along the x – axis or y – axis.
So, it represents a direct proportion.
Yes the number of cups is directly proportional to the number of quarts
Find the Constant of Proportionality :
\(\frac{y}{x}\) = \(\frac{4}{1}\) = 4
\(\frac{y}{x}\) = \(\frac{8}{2}\) = 4
\(\frac{y}{x}\) = \(\frac{12}{3}\) = 4
\(\frac{y}{x}\) = \(\frac{16}{4}\) = 4
The Constant of Proportionality is 4

b) A soup recipe calls for 5 quarts of stock. How many cups of stock does the soup recipe need?
Answer:
$We \know$
\(\frac{y}{x}\) = 4
\(\frac{y}{5}\) = 4 Substituting x = 5
5 ∙ \(\frac{y}{5}\) = 5 ∙ 4 Multiplying bothsides by 5
y = 20
The recipe will need 20 cups of stocks

c) Convert 24 cups of water to quarts of water.
Answer:
$We\ know$
\(\frac{y}{x}\) = 4
\(\frac{24}{x}\) = 4 Substituting x = 24
\(\frac{x}{4}\) ∙ \(\frac{24}{x}\) = \(\frac{x}{4}\) ∙ 4 Multiplying bothsides by \(\frac{x}{4}\)
x = 6
24 cups of water = 6 quarts of water

Question 39.
A printer takes 2.4 seconds longer to print a page in color than a page in black and white. A page in black and white can be printed in 4 seconds.
There are (-\(\frac{5}{8}\)w + 6) color pages and (1.2w + 5) black and white pages to print. (Chapters 3, 4)
Answer:
The printer takes 4 seconds to print a page in black and white.
So, to print a page in color, the printer wilitake = 4 + 2.4 = 6.4 seconds
Number of pages to print in Blackund White 1.2w+ 5
Number of pages to print in Color = \(\frac{5}{8}\)w + 6

a) How long does it take to print all the pages?
Answer:
4 (1.2w + 5) + 6.4 (\(\frac{5}{8}\)w + 6)
= 4(1.2w) + 4(5) + 6.4 (\(\frac{5}{8}\)w) + 6.4(6) Use Distributive Property
= 4.8w + 20 + 4w + 38.4 Multiply
= 4.8w + 4w + 20 + 38.4 Group like terms
= (8.8w + 58.4) seconds

b) If w = 40, how long does it take to print all the pages?
Answer:
8.8w + 58.4
= 8.8(40) + 58.4 Substituting w = 40
= 352 + 58.4 Multiply
= 410.4 seconds

Question 40.
Jason has to choose between two offers of a gym club membership as shown below. (Chapter 4)

Answer:
Gym A = $55 per month membership fee plus $15 per hour of training with a personal trainer.
${\color{#4257b2} Gym\ B) = $220\ per\ month\ membership\ fee\ and\ training\ with\ a\ personal\ trainer\ at\ no\ extra\ cost $
a) After how many hours of training per month would Gym B be a better deal than Gym A?
Answer:
55 + 15x > 220
55 + 15x – 55 > 220 — 55 Subtract 35 from both sides
15x > 165 Simplify
\(\frac{15 x}{15}\) > \(\frac{165}{15}\) Divide both sides by 15
x > 11
After 11 hours of training per month Gym B would be a better deal than Gym A

b) If Jason plans to train for at least 12 hours per month, which gym club membership should he take up? Explain your answers.
Answer:
Gym A:
55 + 15 • 12
= 55 + 180 Multiply
= 235
Gym B:
220
Jason should take membership of Gym B since it is cheaper if he plans to train for at least 12 hours per month

Question 41.
A commission is an amount of money earned by a sales person, based on the amount of sales the person makes. At a particular home-improvement store, the commission made, C, is directly proportional to the amount of sales, S. A sales person earns $198 when he makes total sales of $3,600. (Chapter 5)
Answer:
Commission (C) = $198
Sales (S) = $3600

a) Write a direct proportion equation that relates C and 5. Then express the store’s commission rate as a percent.
Answer:
C is directly proportional to S :
\(\frac{C}{S}\) = \(\frac{198}{3600}\)
\(\frac{C}{S}\) = \(\frac{11}{200}\)
S ∙ \(\frac{C}{S}\) = \(\frac{11}{200}\) ∙ S Multiply both sides by S
C = \(\frac{11}{200}\)S
Express the store’s commission rate as a percent
C is directly proportional to S :
\(\frac{C}{S}\) = \(\frac{11}{200}\)
\(\frac{C}{S}\) = 0.055
\(\frac{C}{S}\) = 0.055 ∙ 100
\(\frac{C}{S}\) = 5.5%

b) Find the amount of sales made if his commission is $297.
Answer:
We know C = \(\frac{11}{200}\)S,
297 = \(\frac{11}{200}\)S Substituting C = 297
\(\frac{200}{11}\) ∙ 297 = \(\frac{200}{11}\) ∙\(\frac{11}{200}\)S Multiplying both sides by \(\frac{200}{11}\)
S = 5400 Simplify
He made a saie of amount $5400 if his commission is $297

Question 42.
Amy and her friends want to equally share the cost of David’s birthday gift. They plan to buy a baseball glove that costs $79.98. The amount of money that each has to contribute, C, is inversely proportional to the number of people sharing the cost, n. (Chapter 5)
Answer:
Cost of baseball gloves = $79.98
Amount of money that each has to contribute = C
Number of people sharing the cost = n
a) Write an inverse proportion equation that relates C and n.
Answer:
Inverse proportion equation :
C ∙ n = 79.98
Cn = 79.98 Multiplying
\(\frac{C n}{n}\) = \(\frac{79.98}{n}\) Divide both sides by n
C = \(\frac{79.98}{n}\)

b) How much will each person have to pay if 6 people are sharing the cost?
Answer:
n = 6 and C = \(\frac{79.98}{n}\),
C = \(\frac{79.98}{6}\) Substituting n = 6
C = 13.33
Each person has to contribute $13.33 if 6 person are sharing the cost.

Question 43.
The time it takes Tim to cycle to his destination varies inversely as his cycling speed in miles per hour. The graph shows the relationship between y and x. (Chapter 5)

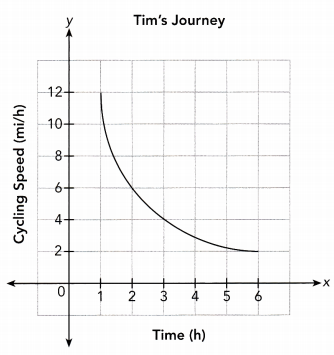
a) Find the constant of proportionality. What does this value represent in this situation?
Answer:
Use the point (1, 12) from the graph to find the constant of proportionality.
x • y = 1 • 12 Choose the point (1, 12)
xy = 12 Multiply
The constant of proportionality is 12
This value represents the distance’ traveled by Tim

b) Write an equation that relates speed and time taken.
Answer:
Use the point (1, 12) from the graph to find the constant of proportionality.
x • y = 1 • 12 Choose the point (1, 12)
xy = 12 Multiply

c) Explain what the point (1, 12) represents in this situation.
Answer:
It means that when Tim cycle at a speed of 12 miles per hour he will reach his destination in 1 hour.

d) How long does it take Tim to reach his destination if he decreases his speed to 6 miles per hour?
Answer:
From the graph :
If Tim cycle at a speed of 6 miles per hour he will reach his destination in 2 hour.

Question 44.
Two-thirds of the capacity of jar A is equivalent to eight-fifteenths of the capacity of jar B. Suppose the full capacity of jar B is (6x – 3) liters. (Chapters 3, 4)
a) What is the full capacity of jar A in terms of x?
Answer:
Let the full capacity of Tank A be A
Let the full capacity of Tank B be B

Two — third of the capacity of Jar A is equivalent to eight — fifteenths of the capacity of jar B :
\(\frac{2}{3}\) ∙ A = \(\frac{8}{15}\) ∙ B Multiplying both sides by \(\frac{3}{2}\)
A = \(\frac{4}{5}\) ∙ B Simplifying
A = \(\frac{4}{5}\) ∙ (6x – 3) Substituting B = (6x – 3)
A = \(\frac{4}{5}\)(6x) – \(\frac{4}{5}\)(3) Using Distributive Property
A = \(\frac{24}{5}\)x – \(\frac{12}{5}\) Multiplying
A = \(\frac{24 x-12}{5}\)

b) If the capacity of jar A is 18 liters, what is the value of x?
Answer:
A = \(\frac{24 x-12}{5}\)
A = \(\frac{24 x-12}{5}\) Substituting A = 18
5 ∙ 18 = 5 ∙ \(\frac{24 x-12}{5}\) Multiplying both sides by 5
90 = 24x – 12 Simplifying
90 + 12 = 24x – 12 + 12 Add 12 to both sides
24x = 102 Simplifying
\(\frac{24 x}{24}\) = \(\frac{102}{24}\) Divide both sides by 24
x = 4.25

Question 45.
A rectangle measures 12 inches by 8 inches. The length of the rectangle is increased by r percent while the width remains unchanged. (Chapters 3, 4)
Answer:
Expanded Length = (12 + \(\frac{12}{100}\)r) inches
Width = 8 inches
a) Write an algebraic expression of the area of the expanded rectangle.
Answer:
Algebraic Expression for the area of the expanded rectangle
Area
= Length ∙ Width
= (12 + \(\frac{12}{100}\)r) ∙ 8
= (12 + 0.12r) ∙ 8
= 8(12) + 8(0.12r)
= (96 + 0.96r) square inches

b) If the area of the expanded rectangle is 120 square inches, find the value of r.
Answer:
Area = 120 square inches
96 + 0.96r = 120
96 + 0.96r – 96 = 120 – 96 Subtract 96 from both suies
0.96r = 24 Simplify
\(\frac{0.96 r}{0.96}\) = \(\frac{24}{0.96}\)
Divide both sides by 0.96
r = 25