This handy Math in Focus Grade 5 Workbook Answer Key Chapter 12 Practice 3 Vertical Angles provides detailed solutions for the textbook questions.
Math in Focus Grade 5 Chapter 12 Practice 3 Answer Key Vertical Angles
Complete.
Question 1.
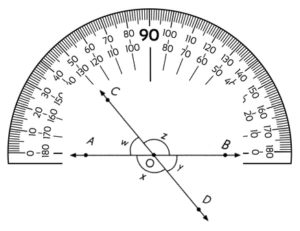
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) meet at O. Use a protractor to find unknown angle measure
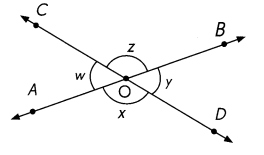
m∠w = _______
m∠x = __________
m∠y = _____
m∠z = __________
m∠____ = m∠______
∠___________ and ∠___________ are vertical angles.
m∠____ = m∠______
∠___________ and ∠___________ are vertical angles.
Answer:
m∠w = 50°
m∠x = 130° = 180 ° – 50°
m∠y = 50°
m∠z = 130°
m∠w = m∠y
Vertical angles are a pair of opposite angles formed by intersecting lines
∠w and ∠y are vertical angles.
m∠x = m∠z
∠x and ∠z are vertical angles.
Explanation:
As can be seen from the figure above, when two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.
Question 2.
\(\overleftrightarrow{X Z}\) and \(\overleftrightarrow{V W}\) meet at Y. Use a protractor to find unknown angle measures.
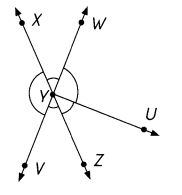
m∠XYW = _______
m∠WYU = __________
m∠UYZ = _____
m∠ZYV = __________
m∠VYX = ______
∠___________ and ∠___________ are vertical ongles.
∠___________ and ∠___________ are vertical angles.
Answer:
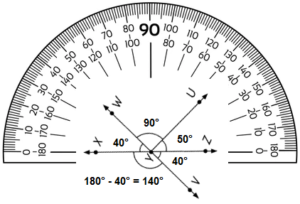
m∠XYW = 40°
m∠WYU = 90°
m∠UYZ = 50°
m∠ZYV = 40°
m∠VYX = 140°
∠XYW and ∠VYZ are vertical ongles.
∠WYZ and ∠XYV are vertical angles.
Explanation:
As can be seen from the figure above, when two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.
Complete.
Question 3.
Look at the star and its marked angles. In the table below, write three sets of:
a. angles on a line,
b. angles at a point,
c. vertical angles.
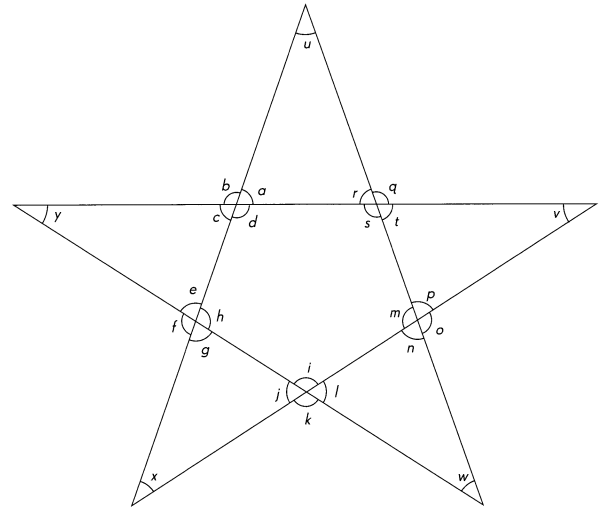
Answer:
Draw.
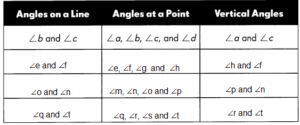
Explanation:
The common point where two rays meet is called the vertex and the rays are called arms of the angle or Angle on lines.
Angles on line add upto 180°
An angle is measured with reference to a circle with its center at the common endpoint of the rays.
Hence, the sum of angles at a point is always 360°
When two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.
Question 4.
Draw rays at P to form
a. an angle whose measure forms a sum of 180° with the measure of ∠x,
Answer:
x= 30°
30° x 6 = 180°
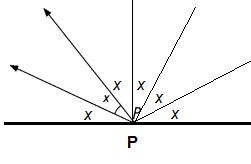
Explanation:
The common point where two rays meet is called the vertex and the rays are called arms of the angle or Angle on lines.
Angles on line add upto 180°
b. an angle whose measure is equal to the measure of ∠x.
(Do not use a protractor to draw the angles.)
a. 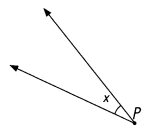
b. 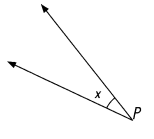
Answer: 30°
Explanation:
An angle measures less than 90 degrees is called acute angle.
Find the unknown angle measures.
Question 5.
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) meet at O. Find the measure of ∠COB.
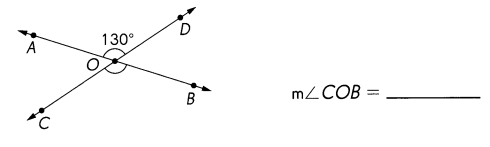
Answer:
m∠COB = 130°
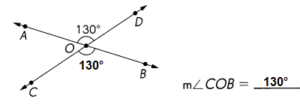
Explanation:
180 – 130 = 50°
Vertical angles are a pair of opposite angles formed by intersecting lines.
∠AOD and ∠COB are vertical angles.
m∠AOD = m∠COB = 130°
Question 6.
\(\overleftrightarrow{E F}\) and \(\overleftrightarrow{G H}\) meet at O. Find the measures of ∠GOF and ∠EOH.
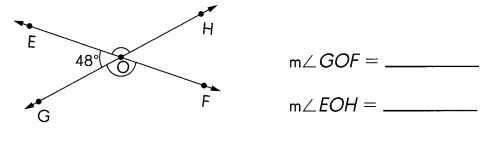
Answer:
m∠GOF = 132° and
m∠EOH = 132°
Explanation:
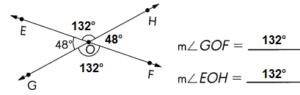
180° – 48° = 132°
Vertical angles are a pair of opposite angles formed by intersecting lines
∠GOF and ∠EOH are vertical angles.
m∠GOF = m∠EOH = 132°
Question 7.
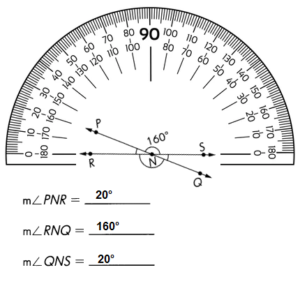
\(\overleftrightarrow{R S}\) and \(\overleftrightarrow{P Q}\) meet at N. Find the measures of ∠PNR, ∠RNQ, and ∠QNS.
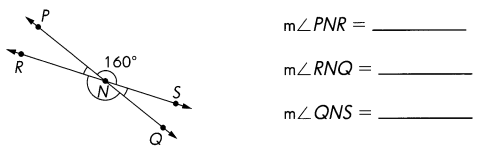
Answer:
m∠PNR = 20°
m∠RNQ = 160°
m∠QNS = 20°
Explanation:
∠PNR = 180° – 160° = 20°
Vertical angles are a pair of opposite angles formed by intersecting lines
Find the unknown angle measures.
Question 8.
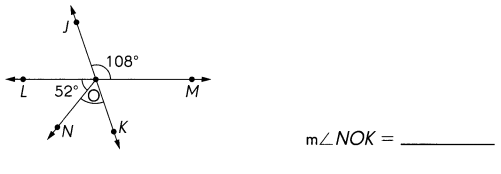
\(\overleftrightarrow{J K}\) and \(\overleftrightarrow{L M}\) meet at O. Find the measure of ∠NOK.
Answer:
∠NOK = 56°
Explanation:
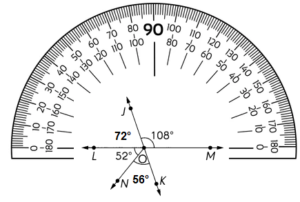
∠LOJ = 180° – 108° = 72°
∠NOK = 180° -(52° + 72°)
=180° – 124°
=56°
Question 9.
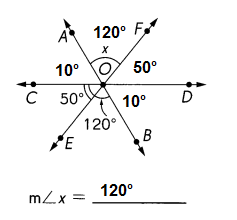
\(\overleftrightarrow{A B}\), \(\overleftrightarrow{C D}\) and \(\overleftrightarrow{E F}\) meet at O. Find the measure of ∠x.
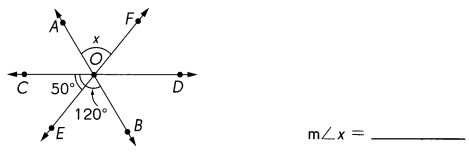
Answer:
m∠x = 120°
Explanation:
As can be seen from the figure below, when two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.
∠AOF and ∠EOB are vertical angles
Question 10.
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) meet at O. Find the measure of ∠w.
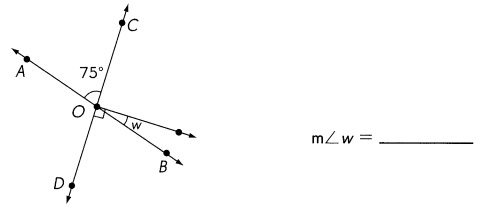
Answer:
m∠w = 75°
Explanation:
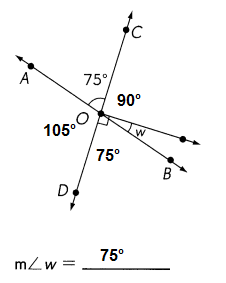
As can be seen from the figure above, when two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.
Find the unknown angle measures.
Question 11.
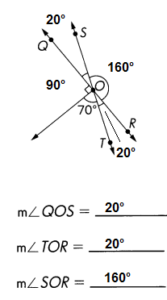
\(\overleftrightarrow{Q R}\) and \(\overleftrightarrow{S T}\)meet at O. Find the measures of ∠QOS, ∠TOR, and ∠SOR.
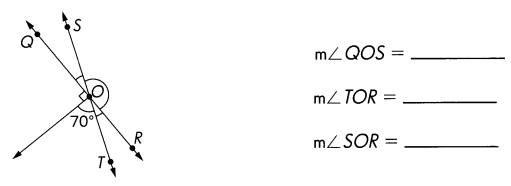
Answer:
m∠QOS = 20°
m∠TOR= 20°
m∠SOR = 160°
Explanation:
As can be seen from the figure below, when two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.
Question 12.
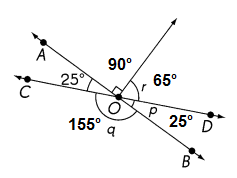
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\)meet at O. Find the measures of ∠p, ∠q, and ∠r.
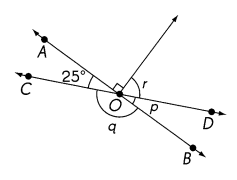
m∠p = ____
m∠q = ____
m∠r = ____
Answer:
m∠p = 25°
m∠q = 155°
m∠r = 65°
Explanation:
As can be seen from the figure below, when two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.
Question 13.
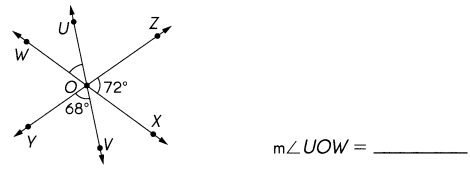
\(\overleftrightarrow{U V}\), \(\overleftrightarrow{W X}\), and \(\overleftrightarrow{Y Z}\) meet at O. Find the measure of ∠UOW.
Answer:
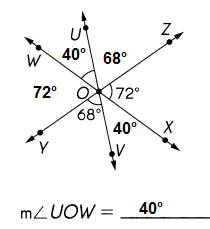
Explanation:
when two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.
68° + 72° = 140
∠UOW = 180° -140° = 40°
Question 14.
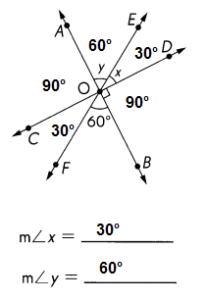
\(\overleftrightarrow{A B}\), \(\overleftrightarrow{C D}\), and \(\overleftrightarrow{E F}\) meet at O. Find the measures of ∠x and ∠y.
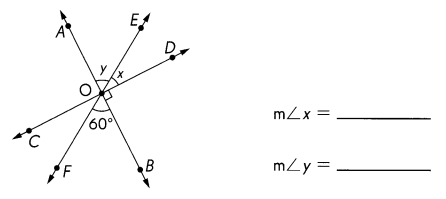
Answer:
m∠x = 30°
m∠y = 60°
Explanation:
∠AOB = 180° – (∠AOC + ∠FOB)
= 180° – (90° + 60°)
= 180° – 150° = 30°