Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 1 Lesson 1.3 Introducing Irrational Numbers to finish your assignments.
Math in Focus Grade 7 Course 2 A Chapter 1 Lesson 1.3 Answer Key Introducing Irrational Numbers
Math in Focus Grade 7 Chapter 1 Lesson 1.3 Guided Practice Answer Key
Hands-On Activity
Materials:
- paper
- ruler
- scissors
Find the value of \(\sqrt{2}\) using a square.
Work in pairs.
Step 1.
Draw a square that has a length of 2 inches on a piece of paper. Then cut out the square.
Step 2.
Find the area of the square (square A).
Step 3.
Fold the four vertices of square A towards the center to form square B as shown below.
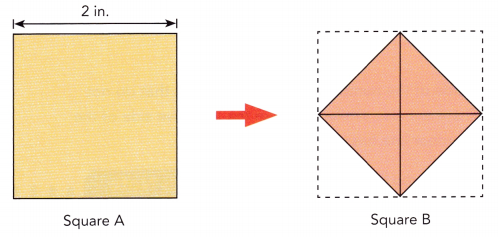
Step 4.
State how the areas of square A and square B are related. State the area of square B. How can you represent the length of a side of square B?
Step 5.
Using your answer in step 4, find the length of a side of square B with a calculator. Round your answer to 2 decimal places.
Math Journal
Place an edge of square B alongsi& a ruler to measure its length. Explain why the reading from the ruler is different from the answer in step 5.
Copy and complete.
Question 1.
Graph \(\sqrt{5}\) on the number line using rational approximations.
Which two whole numbers is \(\sqrt{5}\) between? Justify your reasoning. Using a calculator, \(\sqrt{5}\) = ![]() .
.
Graph an interval where \(\sqrt{5}\) is located.
The value of \(\sqrt{5}\) with two decimal places is ![]()
![]() is closer to
is closer to ![]() than to
than to ![]() . So, \(\sqrt{5}\) is located closer to
. So, \(\sqrt{5}\) is located closer to ![]() .
.

By using an approximate value of \(\sqrt{5}\), locate \(\sqrt{5}\) on the number line.

Answer:
The \(\sqrt{5}\) is between two whole numbers. The two whole numbers are 2 and 3.
By using calculator \(\sqrt{5}\) = 2.236067977….
The value of \(\sqrt{5}\) with two decimal places is 2.24.
The decimal 2.24 is closer to 2.2 than to 2.3.
So, \(\sqrt{5}\) is located closer to 2.2.

By using an approximate value of \(\sqrt{5}\), located \(\sqrt{5}\) on the number line as we can observe in the below image.

Copy and complete.
Question 2.
Graph –\(\sqrt{2}\) on the number line using rational approximations.
Which two integers is –\(\sqrt{2}\) between? Justify your reasoning. Using a calculator, –\(\sqrt{2}\) = ![]() .
.
Graph an interval where –\(\sqrt{2}\) is located.
The value of –\(\sqrt{2}\) with two decimal places is ? ![]() .
.
![]() is closer to
is closer to ![]() than to
than to ![]() . So, –\(\sqrt{2}\) is located closer to ?
. So, –\(\sqrt{2}\) is located closer to ? ![]()

By using an approximate value of –\(\sqrt{2}\), locate –\(\sqrt{2}\) on the number line.

Answer:
The –\(\sqrt{2}\) is between two whole numbers. The two whole numbers are -1 and -2.
By using calculator –\(\sqrt{2}\) = -1.414213562…..
The value of –\(\sqrt{2}\) with two decimal places is -1.41.
The decimal -1.41 is closer to -1.4 than to -1.5.
So, –\(\sqrt{2}\) is located closer to -1.4.

By using an approximate value of –\(\sqrt{2}\), located –\(\sqrt{2}\) on the number line as we can observe in the below image.

Solve.
Question 3.
Graph –\(\sqrt{7}\) on the number line using rational approximations.
Answer:
The –\(\sqrt{7}\) is between two whole numbers. The two whole numbers are -2 and -3.
By using calculator –\(\sqrt{7}\) = -2.645751311…..
The value of –\(\sqrt{7}\) with two decimal places is -2.64.
The decimal -2.64 is closer to -2.6 than to -2.7.
So, –\(\sqrt{7}\) is located closer to -2.6.
By using an approximate value of –\(\sqrt{7}\), located –\(\sqrt{7}\) on the number line as we can observe in the below image.
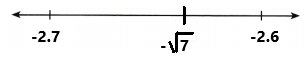
Math in Focus Course 2A Practice 1.3 Answer Key
Locate each positive irrational number on the number line using rational approximations. First tell which two whole numbers the square root is between.
Question 1.
\(\sqrt{3}\)
Answer:
The \(\sqrt{3}\) is between two whole numbers. The two whole numbers are 1 and 2.
By using calculator \(\sqrt{3}\) = 1.732050807….
The value of \(\sqrt{3}\) with two decimal places is 1.73.
The decimal 1.73 is closer to 1.7 than to 1.8.
So, \(\sqrt{3}\) is located closer to 1.7.

By using an approximate value of \(\sqrt{3}\), the positive irrational number \(\sqrt{3}\) is located on the number line as we can observe in the above image.
Question 2.
\(\sqrt{7}\)
Answer:
The \(\sqrt{7}\) is between two whole numbers. The two whole numbers are 2 and 3.
By using calculator \(\sqrt{7}\) = 2.645751311….
The value of \(\sqrt{7}\) with two decimal places is 2.64.
The decimal 2.64 is closer to 2.6 than to 2.7.
So, \(\sqrt{7}\) is located closer to 2.6.

By using an approximate value of \(\sqrt{7}\), the positive irrational number \(\sqrt{7}\) is located on the number line as we can observe in the above image.
Question 3.
\(\sqrt{11}\)
Answer:
The \(\sqrt{11}\) is between two whole numbers. The two whole numbers are 3 and 4.
By using calculator \(\sqrt{11}\) = 3.316624790….
The value of \(\sqrt{11}\) with two decimal places is 3.31.
The decimal 3.31 is closer to 3.3 than to 3.4.
So, \(\sqrt{11}\) is located closer to 3.3.

By using an approximate value of \(\sqrt{11}\), the positive irrational number \(\sqrt{11}\) is located on the number line as we can observe in the above image.
Question 4.
\(\sqrt{26}\)
Answer:
The \(\sqrt{26}\) is between two whole numbers. The two whole numbers are 5 and 6.
By using calculator \(\sqrt{26}\) = 5.099019513….
The value of \(\sqrt{26}\) with two decimal places is 5.09.
The decimal 5.09 is closer to 5.1 than to 5.0.
So, \(\sqrt{26}\) is located closer to 5.1.

By using an approximate value of \(\sqrt{26}\), the positive irrational number \(\sqrt{26}\) is located on the number line as we can observe in the above image.
Question 5.
\(\sqrt{34}\)
Answer:
The \(\sqrt{34}\) is between two whole numbers. The two whole numbers are 5 and 6.
By using calculator \(\sqrt{34}\) = 5.830951894….
The value of \(\sqrt{34}\) with two decimal places is 5.83.
The decimal 5.83 is closer to 5.8 than to 5.9.
So, \(\sqrt{34}\) is located closer to 5.8.

By using an approximate value of \(\sqrt{34}\), the positive irrational number \(\sqrt{34}\) is located on the number line as we can observe in the above image.
Question 6.
\(\sqrt{48}\)
Answer:
The \(\sqrt{48}\) is between two whole numbers. The two whole numbers are 6 and 7.
By using calculator \(\sqrt{48}\) = 6.928203230….
The value of \(\sqrt{48}\) with two decimal places is 6.92.
The decimal 6.92 is closer to 6.9 than to 7.0.
So, \(\sqrt{48}\) is located closer to 6.9.

By using an approximate value of \(\sqrt{48}\), the positive irrational number \(\sqrt{48}\) is located on the number line as we can observe in the above image.
Locate each negative irrational number on the number line using rational approximations. First tell which two integers the square root is between.
Question 7.
–\(\sqrt{5}\)
Answer:
The –\(\sqrt{5}\) is between two integers. The two integers are -2 and -3.
By using calculator –\(\sqrt{5}\) = -2.236067977…..
The value of –\(\sqrt{5}\) with two decimal places is -2.23.
The decimal -2.23 is closer to -2.2 than to -2.3.
So, –\(\sqrt{5}\) is located closer to -2.2.
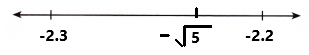
By using an approximate value of –\(\sqrt{5}\), the negative irrational number –\(\sqrt{5}\) is located on the number line as we can observe in the above image.
Question 8.
–\(\sqrt{6}\)
Answer:
The –\(\sqrt{6}\) is between two integers. The two integers are -2 and -3.
By using calculator –\(\sqrt{6}\) = -2.449489742…..
The value of –\(\sqrt{6}\) with two decimal places is -2.44.
The decimal -2.44 is closer to -2.4 than to -2.5.
So, –\(\sqrt{6}\) is located closer to -2.4.
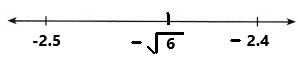
By using an approximate value of –\(\sqrt{6}\), the negative irrational number –\(\sqrt{6}\) is located on the number line as we can observe in the above image.
Question 9.
–\(\sqrt{17}\)
Answer:
The –\(\sqrt{17}\) is between two integers. The two integers are -4 and -5.
By using calculator –\(\sqrt{17}\) = -4.123105625…..
The value of –\(\sqrt{17}\) with two decimal places is -4.12.
The decimal -4.12 is closer to -4.1 than to -4.2.
So, –\(\sqrt{17}\) is located closer to -4.1.

By using an approximate value of –\(\sqrt{17}\), the negative irrational number –\(\sqrt{17}\) is located on the number line as we can observe in the above image.
Question 10.
–\(\sqrt{26}\)
Answer:
The –\(\sqrt{26}\) is between two integers. The two integers are -5 and -6.
By using calculator –\(\sqrt{26}\) = -5.099019513….
The value of –\(\sqrt{26}\) with two decimal places is -5.09.
The decimal -5.09 is closer to -5.1 than to -5.0.
So, –\(\sqrt{26}\) is located closer to -5.1.

By using an approximate value of –\(\sqrt{26}\), the negative irrational number –\(\sqrt{26}\) is located on the number line as we can observe in the above image.
Question 11.
–\(\sqrt{53}\)
Answer:
The –\(\sqrt{53}\) is between two integers. The two integers are -7 and -8.
By using calculator –\(\sqrt{53}\) = -7.280109889….
The value of –\(\sqrt{53}\) with two decimal places is -7.28.
The decimal -7.28 is closer to -7.3 than to -7.2.
So, –\(\sqrt{53}\) is located closer to -7.3.
![]()
By using an approximate value of –\(\sqrt{53}\), the negative irrational number –\(\sqrt{53}\) is located on the number line as we can observe in the above image.
Question 12.
–\(\sqrt{80}\)
Answer:
The –\(\sqrt{80}\) is between two integers. The two integers are -8 and -9.
By using calculator –\(\sqrt{80}\) = -8.944271909….
The value of –\(\sqrt{80}\) with two decimal places is -8.94.
The decimal -8.94 is closer to -8.9 than to -9.0.
So, –\(\sqrt{80}\) is located closer to -8.9.
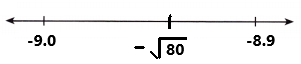
By using an approximate value of –\(\sqrt{80}\), the negative irrational number –\(\sqrt{80}\) is located on the number line as we can observe in the above image.
Use a calculator. Locate each irrational number to 3 decimal places on the number line using rational approximations.
Question 13.
\(\sqrt{47}\)
Answer:
By using calculator \(\sqrt{47}\) = 6.855654600….
The value of \(\sqrt{47}\) with three decimal places is 6.855.
The decimal 6.855 is closer to 6.86 than to 6.85.
So, \(\sqrt{47}\) is located closer to 6.86.
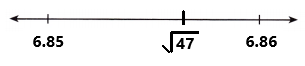
The given irrational number \(\sqrt{47}\) is located on the number line by using rational approximation as we can observe in the above image.
Question 14.
–\(\sqrt{15}\)
Answer:
By using calculator –\(\sqrt{15}\) = –3.872983346….
The value of –\(\sqrt{15}\) with three decimal places is –3.872.
The decimal -3.872 is closer to –3.87 than to –3.88.
So, –\(\sqrt{15}\) is located closer to -3.87.

The given irrational number –\(\sqrt{15}\) is located on the number line by using rational approximation as we can observe in the above image.
Question 15.
![]()
Answer:
By using calculator ![]() = 4.54683594….
= 4.54683594….
The value of ![]() with three decimal places is 4.546.
with three decimal places is 4.546.
The decimal 4.546 is in between 4.5 and 4.6.
So, ![]() is located on 4.55.
is located on 4.55.
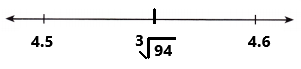
The given irrational number ![]() is located on the number line by using rational approximation as we can observe in the above image.
is located on the number line by using rational approximation as we can observe in the above image.
Locate each irrational number on the number line using rational approximations.
Question 16.
\(\sqrt{101}\)
Answer:
By using calculator \(\sqrt{101}\) = 10.049875….
The value of \(\sqrt{101}\) with two decimal places is 10.04.
The decimal 10.04 is closer to 10 than to 10.1.
So, \(\sqrt{101}\) is located closer to 10.
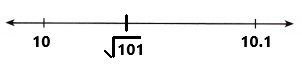
The given irrational number \(\sqrt{101}\) is located on the number line by using rational approximation as we can observe in the above image.
Question 17.
–\(\sqrt{132}\)
Answer:
By using calculator –\(\sqrt{132}\) = – 11.489125….
The value of –\(\sqrt{132}\) with two decimal places is –11.48.
The decimal -11.48 is closer to –11.5 than to –11.4.
So, –\(\sqrt{132}\) is located closer to –11.5.

The given irrational number –\(\sqrt{132}\) is located on the number line by using rational approximation as we can observe in the above image.
Question 18.
\(\sqrt{2,255}\)
Answer:
By using calculator \(\sqrt{2,255}\) = 47.4868….
The value of \(\sqrt{2,2551}\) with two decimal places is 47.48.
The decimal 47.48 is closer to 47.5 than to 47.4.
So, \(\sqrt{2,255}\) is located closer to 47.5.
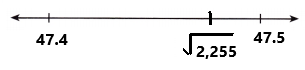
The given irrational number \(\sqrt{2,255}\) is located on the number line by using rational approximation as we can observe in the above image.
Solve.
Question 19.
Locate the value of the constant, π, on the number line using rational numbers.
Answer:
We know that π = 3.14159265

In the above image we can observe the value of the constant, π, is located on the number line using rational numbers.
Question 20.
3.1416 and \(\frac{22}{7}\) are two rational approximate values of π.
a) Graph 3.1416, \(\frac{22}{7}\), and π on the number line.
b) Which of the two rational approximate values is closer to π?
Answer:
a)We know that 22/7 = 3.1428, π = 3.14159
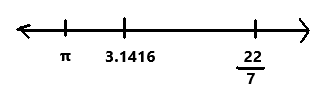
In the above image we can observe 3.1416, 22/7 and π on the number line.
b) The two rational approximate values closer to π are 3.1416 and 22/7.
Question 21.
A triangle is cut from a square as shown in the diagram. The area of the square is 59 square inches. Approximate the height of the triangle to 3 decimal places.
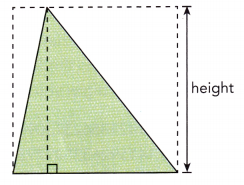
Answer:
Question 22.
Math Journal When do you need to approximate an irrational number with a rational value? Explain and illustrate with an example.
Answer: