Math in Focus Grade 6 Chapter 14 Lesson 14.1 Answer Key Mean

This handy Math in Focus Grade 6 Workbook Answer Key Chapter 14 Lesson 14.1 Mean detailed solutions for the textbook questions.

Math in Focus Grade 6 Course 1 B Chapter 14 Lesson 14.1 Answer Key Mean

Math in Focus Grade 6 Chapter 14 Lesson 14.1 Guided Practice Answer Key

Complete.

Four boys have heights of 154 centimeters, 157 centimeters, 160 centimeters, and 165 centimeters.

Question 1.
What is the total height of the four boys?
Total height
= + + +
= cm
The total height of the four boys is ______ centimeters.
Answer:
636 centimeters.

Explanation:
It is given that four boys have heights of 154 centimeters, 157 centimeters, 160 centimeters, and 165 centimeters.
We know that, Total height of four boys = The sum of the heights of each boy.
So, The total height of the four boys = 154 cm + 157 cm + 160 cm + 165 cm = 636 cm
Hence, We can conclude that,
The total height of the four boys is 636 centimeters.

Question 2.
What is the mean height of the four boys?
Mean height
= \(\frac{\text { total height }}{\text { number of boys }}\)
= ÷
= cm
The mean height of the four boys is ______ centimeters.
Answer:
159 centimeters.

Explanation:
From Question 1, We can observe that,
The total height of the four boys is 636 centimeters
Now, We know that,
The mean height of the four boys = \(\frac{\text {The total height of four boys}}{\text {The number of boys}}\)
So, The mean height of the four boys = \(\frac{636}{4}\)
= 636 ÷ 4
Now, by using the Long Division,

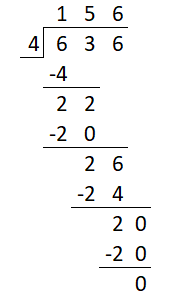
Hence, from the above,
We can conclude that the mean height of the four boys is: 159 centimeters.

Complete. Use the data in the table.

The table shows the temperature at noon from Monday to Friday in one city.

Question 3.
What was the mean temperature at noon from Monday to Friday?
Mean temperature

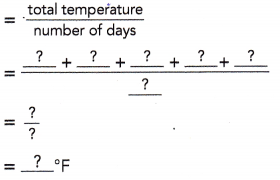
The mean temperature at noon from Monday to Friday was °F.
Answer:
50.8°F

Explanation:
The given table is:

We know that,
Mean = \(\frac{\text {The sum of the values}}{\text {The number of values}}\)
So, The mean temperature at noon from Monday to Friday = \(\frac{52°F + 51°F + 49°F + 48°F + 54°F}{5}\)
= \(\frac{254°F}{5}\)
Now, by using the Long Division,

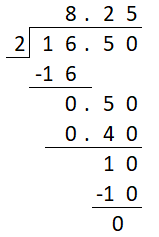
Hence, from the above,
We can conclude that the mean temperature at noon from Monday to Friday was 50.8°F

Complete. Use the data in the dot plot.

A group of volunteers was selling coupons to raise money for a food pantry. The dot plot on the right shows the number of coupons sold by each volunteer. Each dot represents 1 volunteer.

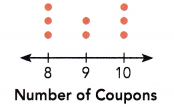
Question 4.
volunteers sold 8 coupons each. × = coupons sold
Answer:
24 coupons sold.

Explanation:
It is given that, A group of volunteers was selling coupons to raise money for a food pantry.
The dot plot shows the number of coupons sold by each volunteer. Each dot represents 1 volunteer.
Now, The given figure is:

From the given figure we can observe that,
The number of coupons sold by 3 Volunteers = 3 × (The number of coupons sold by each volunteer)
= 3 × 8
= 24 coupons
Hence, from the above We can conclude that,
3 volunteers sold 8 coupons each.
8 × 3 = 24 coupons sold.

Question 5.
volunteers sold 9 coupons each. × = coupons sold
Answer:
18 coupons sold.

Explanation:
It is given that, A group of volunteers was selling coupons to raise money for a food pantry.
The dot plot shows the number of coupons sold by each volunteer. Each dot represents 1 volunteer.
Now, The given figure is:

From the given figure we can observe that,
The number of coupons sold by 2 Volunteers = 2 × (The number of coupons sold by each volunteer)
= 2 × 9
= 18 coupons
Hence, from the above we can conclude that,
2 volunteers sold 9 coupons each.
2 × 9 = 18 coupons sold.

Question 6.
volunteers sold 10 coupons each. × = coupons sold
Answer:
30 coupons sold.

Explanation:
It is given that, A group of volunteers was selling coupons to raise money for a food pantry.
The dot plot shows the number of coupons sold by each volunteer.
Each dot represents 1 volunteer.
Now, The given figure is:

From the given figure we can observe that,
The number of coupons sold by 3 Volunteers = 10 × (The number of coupons sold by each volunteer)
= 10 × 3
= 30 coupons
Hence, from the above we can conclude that,
3 volunteers sold 10 coupons each.
10 × 3 = 30 coupons sold.

Question 7.
coupons were sold altogether.
Answer:
72 coupons.

Explanation:
From Questions 4, 5, and 6,
We can observe that, the total number of coupons sold 24 + 18 + 30 = 72 coupons
Hence, from the above we can conclude that,
72 coupons were sold altogether.

Question 8.
There were _____ volunteers altogether.
Answer:
8 volunteers.

Explanation:
The given figure is:

From the given figure we can observe that,
Each dot represents 1 volunteer
So, The total number of volunteers = 3 + 2 + 3 = 8 volunteers
Hence, from the above we can conclude that,
There were 8 volunteers altogether.

Question 9.
The mean number of coupons sold by the group of volunteers was _____.
Answer:
9 coupons.

Explanation:
The given figure is:

The mean number of coupons sold by the group of volunteers = \(\frac{\text {The total number of coupons sold altogether}}{\text {The total number of volunteers}}\)
= \(\frac{72}{8}\)
= 9
Hence, from the above we can conclude that,
The mean number of coupons sold by the group of volunteers was 9 coupons.

Solve.

Question 10.
Jay’s mean score for four quizzes is 8. His scores for the first three quizzes are 7.5, 8, and 9. What is Jay’s score for the last quiz?
Total score for the four quizzes = mean score × number of quizzes
= ×
=
Total score for the first three quizzes = + +
=
– =
Jay’s score for the last quiz is ______.
Answer:
Jay’s score for the last quiz is 7.5.

Explanation:
It is given that, Jay’s mean score for four quizzes is 8.
His scores for the first three quizzes are 7.5, 8, and 9.
Now we know that,
The total score for the four quizzes = (The mean of the four quizzes) × (The total number of quizzes)
So, The total score for the four quizzes 8 × 4 = 32
The total score for the first three quizzes 7.5 + 8 + 9 = 24.5
So, Jay’s score for the last quiz,
(The total score for the four quizzes) – (The total score for the first three quizzes)
= 32 – 24.5
= 7.5
Hence, from the above we can conclude that,
Jay’s score for the final quiz is 7.5

Question 11.
Sarah’s mean number of points scored for four video games is 7,500. How many points must she score in the fifth video game so that her mean score becomes 7,700?
Answer:
8,500 points.

Explanation:
It is given that, Sarah’s mean number of points scored for four video games is 7,500 and her mean score is 7,700.
We know that,
The total number of points scored by Sarah = (The mean score of Sarah) × (The total number of video games played by Sarah)
The total number of points scored by Sarah = 7,700 × 5
= 38,500 points.
The total number of points scored by Sarah in her four video games = (The mean score of Sarah) ×4
The total number of points scored by Sarah in her four video games = 7,500 × 4
= 30,000 points.
The number of points scored by Sarah in the fifth video game = (The total number of points scored by Sarah) – (The number of points scored by Sarah in her four video games)
= 38,500 – 30,000
= 8,500 points
Hence, from the above we can conclude that,
The number of points scored by Sarah in her fifth video game is 8,500 points.

Hands-On Activity

Finding Mean and Using Mean to Solve Problems

Materials

• centimeter ruler
• blank table

Work in groups of five.

Step 1: Use a centimeter ruler to measure the length of each group member’s hand to the nearest tenth of a centimeter. Record your answers in a copy of the table below.

Step 2: Use your data to answer the following questions.
What is the longest hand length?
What is the shortest hand length?
The mean hand length of the group is _____ centimeters.

Step 3: Math Journal Suppose a new student joins your group and the mean of the hand length of your group increases by 0.3 centimeters. Find the hand length of the new student to the nearest centimeter. Explain how you found your answer.
Answer:

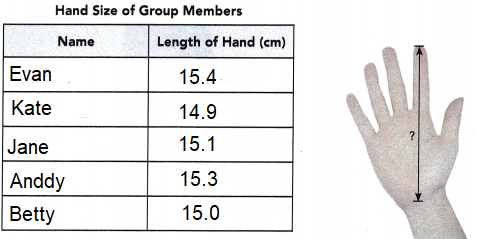
the longest hand length is 15.4 cm
the shortest hand length is 14.9 cm
The mean hand length of the group is 15.14 centimeters.
The hand length of the new student to the nearest centimeter is 17cm.
Explanation:
First by using the ruler find the hand of the students in the class randomly in centimeters.
Then find the longest and shortest hand length from the observations recorded as shown above.
Mean = \(\frac{\text {The sum of the values}}{\text {The number of values}}\)
= \(\frac{(15.4 + 14.9 + 15.1 + 15.3 + 15.0)}{5}\)
= \(\frac{75.7}{5}\)
= 15.14 cm.
If a new student joins the group and the mean of hand length of the group increases by 0.3 cm. Then, the hand length of the new student,
Mean = 15.14 + 0.3 = 15.44 cm
15.44 = \(\frac{(15.4 + 14.9 + 15.1 + 15.3 + 15.0 + x)}{6}\)
= \(\frac{75.7x}{6}\)
x = 15.44 x 6 – 75.7
x = 92.64 – 75.7
x = 16.94
So, the hand length of the new student to the nearest centimeter is 17 cm.

Math in Focus Course 1B Practice 14.1 Answer Key

Find the mean of each data set.

Question 1.
8, 7, 5, 9, 6, 13
Answer:
8

Explanation:
The given data set is:
8, 7, 5, 9, 6, 13
We know that,
Mean = \(\frac{\text {The sum of the total data set}}{\text {The number of digits present in the data set}}\)
The mean of the given data set = \(\frac{8 + 7 + 5 + 9 + 6 + 13}{6}\)
= \(\frac{48}{6}\)
= 8
Hence, from the above we can conclude that,
The mean of the given data set is 8.

Question 2.
72 L, 91 L, 65 L, 81 L, 62 L, 83 L, 75 L, 88 L
Answer:
77.125 L

Explanation:
The given data set is:
72 L, 91 L, 65 L, 81 L, 62 L, 83 L, 75 L, 88 L
We know that,
Mean = \(\frac{\text {The sum of the total data set}}{\text {The number of digits present in the data set}}\)
The mean of the given data set = \(\frac{72 + 91 + 65 + 81 + 62 + 83 + 75 + 88}{8}\)
= \(\frac{617}{8}\)
= 77.125
Hence, from the above we can conclude that,
The mean of the given data set is 77.125 L

Question 3.
21.5 cm, 63.7 cm, 18.9 cm, 34.1 cm, 75.6 cm
Answer:
42.76 cm.

Explanation:
The given data set is:
21.5 cm, 63.7 cm, 18.9 cm, 34.1 cm, 75.6 cm
We know that,
Mean = \(\frac{\text {The sum of the total data set}}{\text {The number of digits present in the data set}}\)
The mean of the given data set = \(\frac{21.5 + 63.7 + 18.9 + 34.1 + 75.6}{5}\)
= \(\frac{213.8}{5}\)
= 42.76
Hence, from the above we can conclude that,
The mean of the given data set is 42.76 cm.

Solve. Show your work.

Question 4.
The number of goals scored by seven forwards in one soccer season was 8, 6, 4, 8, 3, 1, and 5. Find the mean number of goals scored by the seven forwards.
Answer:
5 goals.

Explanation:
It is given that,
The number of goals scored by seven forwards in one soccer season was 8, 6, 4, 8, 3, 1, and 5
We know that,
The mean number of goals scored by the seven forwards = \(\frac{\text {The total sum of the goals scored by seven forwards}}{\text {The number of goals}}\)
The mean number of goals scored by the seven forwards = \(\frac{8 + 6 + 4 + 8 + 3 + 1 + 5}{7}\)
= \(\frac{35}{7}\)
= 5
Hence, from the above we can conclude that,
The mean number of goals scored by the seven forwards is 5 goals.

Question 5.
The lengths of the five ropes are 3.2 meters, 5.2 meters, 2.9 meters, 6.6 meters, and 4.5 meters. Find the mean length of these five ropes.
Answer:
4.48 meters.

Explanation:
It is given that,
The lengths of the five ropes are 3.2 meters, 5.2 meters, 2.9 meters, 6.6 meters, and 4.5 meters
We know that,
The mean length of the five ropes = \(\frac{\text {The total length of the five ropes}}{\text {The number of ropes}}\)
The mean length of the five ropes = \(\frac{3.2 + 5.2 + 2.9 + 6.6 + 4.5}{5}\)
= \(\frac{22.4}{5}\)
= 4.48
Hence, from the above we can conclude that,
The mean length of the five ropes is 4.48 meters.

Question 6.
The masses of six chairs are 34.5 kilograms, 42.6 kilograms, 39.8 kilograms, 40.1 kilograms, 53.4 kilograms, and 33.8 kilograms. Find their mean mass.
Answer:
40.7 kilograms.

Explanation:
It is given that,
The masses of six chairs are 34.5 kilograms, 42.6 kilograms, 39.8 kilograms, 40.1 kilograms, 53.4 kilograms, and 33.8 kilograms.
We know that,
The mean mass of the six chairs = \(\frac{\text {The total mass of the six chairs}}{\text {The number of chairs}}\)
The mean mass of the six chairs = \(\frac{34.5 + 42.6 + 39.8 + 40.1 + 53.4 + 33.8}{6}\)
= \(\frac{244.2}{6}\)
= 40.7 kilograms
Hence, from the above we can conclude that,
The mean mass of the six chairs is 40.7 kilograms.

Use the data in the table to answer the question.

The table shows a sprinter’s times for the 100-meter dash at the first five meets of one season.

Question 7.
What was the sprinter’s meantime for the 100-meter dash at these meets?
Answer:
10.116 s

Explanation:
It is given that,
The table shows a sprinter’s times for the 100-meter dash at the first five meets of one season.
The given table is:

From the above table we can observe that,
The sprinter’s meantime for the 100-meter dash at these meets = \(\frac{\text {The total time taken to complete the 100-meter dash}}{\text {The number of meets}}\)
The sprinter’s meantime for the 100-meter dash at these meets = \(\frac{10.09 + 10.14 + 10.29 + 10.07 + 9.99}{5}\)
= \(\frac{50.58}{5}\)
= 10.116 s
Hence, from the above we can conclude that,
The sprinter’s meantime for the 100-meter dash at these meets is 10.116 s.

Use the data in the dot plot to answer questions 8 and 9

Eight ice hockey teams competed in the quarter-finals of a national championship. The dot plot on the right shows the number of goals scored by each team. Each dot represents 1 team.

Question 8.
What was the total number of goals scored by the eight teams?
Answer:
26 goals.

Explanation:
It is given that,
Eight ice hockey teams competed in the quarter-finals of a national championship.
The dot plot shows the number of goals scored by each team.
Each dot represents 1 team.
The given figure is:

From the given figure we can observe that,
The total number of goals scored by the eight teams = (The total number of teams) × (The total number of goals made by each team)
= (2 × 2) + (3 × 3) + (4 × 2) + (5 × 1)
= 4 + 9 + 8 + 5
= 26 goals
Hence, from the above we can conclude that,
The total number of goals scored by the eight teams is 26 goals.

Question 9.
What was the mean number of goals scored by each team?
Answer:
3 goals.

Explanation:
From Question 8,
We can observe that the total number of goals scored by the eight teams is 26 goals.
We know that the mean number of goals scored by each team,
\(\frac{\text {The total number of goals scored by the eight teams}}{\text {The total number of teams}}\)
The mean number of goals scored by each team = \(\frac{26}{8}\)
= 3.25
≅ 3 goals
Hence, from the above we can conclude that,
The mean number of goals scored by each team is about 3 goals.

Solve. Show your work.

Question 10.
The mean of the five numbers 3, 7, 9, 12, and x is 8. Find the value of x.
Answer:
x = 9

Explanation:
It is given that the mean of the five numbers 3, 7, 9, 12, and x is 8
We know that,
Mean = \(\frac{\text {The sum of the numbers}}{\text {The count of the numbers}}\)
The mean of the five numbers = \(\frac{3 + 7 + 9 + 12 + x}{5}\)
8 = \(\frac{31 + x}{5}\)
31 + x = 8 × 5
x = 40 – 31
x = 9
Hence, the value of x is 9.

Question 11.
The mean of a set of five numbers is 4.8. Given that the sixth number is x and the mean of these six numbers is 5.5, find the value of x.
Answer:
x = 9

Explanation:
It is given that the mean of a set of five numbers is 4.8.
Mean = \(\frac{\text {The sum of the numbers}}{\text {The count of the numbers}}\)
The total sum of the set of five numbers = 4.8 × 5
= 24
The total sum of the set of six numbers 5.5 × 6 = 33
The value of the sixth number (x) = (The total sum of the set of six numbers) – (The total sum of the set of five numbers)
= 33 – 24
= 9
Hence, the value of x is 9.

Question 12.
In a race, the meantime for three runners was 12.4 seconds and the meantime for another six runners was 11.5 seconds. Calculate the meantime for all the nine runners.
Answer:
23.9 seconds.

Explanation:
It is given that, in a race, the meantime for three runners was 12.4 seconds and the meantime for another six runners was 11.5 seconds.
The meantime for all the nine runners = (The meantime for three runners) + (The meantime for six runners)
The meantime for all the nine runners = 12.4 + 11.5
= 23.9 seconds
Hence, the meantime for all the nine runners is 23.9 seconds.

Question 13.
The mean weight of nine apples is 7.5 ounces. Three of the apples have a mean weight of 8 ounces. Find the mean weight of the other six apples.

Answer:
7.25 ounces.

Explanation:
It is given that the mean weight of nine apples is 7.5 ounces.
Three of the apples have a mean weight of 8 ounces
We know that,
The total mean weight of nine apples = (The total mean weight of three apples) + (The total mean weight of six apples)
So, The total weight of six apples = (The total weight of nine apples) – (The total weight of three apples)
= (7.5 × 9) – (8 × 3)
= 67.5 – 24
= 43.5 ounces
The total mean weight of six apples = \(\frac{\text {The total weight of six apples}}{\text {The number of apples}}\)
= \(\frac{43.5}{6}\)
= 7.25 ounces
Hence, the mean weight of the other six apples is 7.25 ounces.

Question 14.
The mean of six numbers is 45. Four of the numbers are 40, 38, 46, and 51. If the remaining two numbers are in the ratio 2 : 3, find the two numbers.
Answer:
38 and 57 are the numbers.

Explanation:
It is given that the mean of six numbers is 45.
Four of the numbers are 40, 38, 46, and 51 and the remaining two numbers are in the ratio 2 : 3
Now, Let
x—–> the missing smaller number
y—-> the missing larger number
We know that,
Mean = \(\frac{\text {The sum of the numbers in the data set}}{\text {The number of values present in the data set}}\)
45 = \(\frac{40 + 35 + 46 + 51 + x + y}{6}\)
40 + 35 + 46 + 51 + x + y = 270
175 + x + y = 270
x + y = 95  —–> Equation A
It is also given that, \(\frac{x}{y}\) = \(\frac{2}{3}\)
x = \(\frac{2}{3}\)y  —–> equation B
Now, substitute equation B in equation A and solve for y.
So, \(\frac{2}{3}\)y + y = 95
y (1 + \(\frac{2}{3}\) ) = 95
\(\frac{5}{3}\)y = 95
y = 95 × \(\frac{3}{5}\)
y = 19 × 3
y = 57
Now, substitute the value of y in Equation B.
So, x = \(\frac{2}{3}\) × 57
x = 2 × 19
x = 38
Hence, the two numbers are 38 and 57.

Question 15.
A data set consists of three numbers, a, b, and c. Write an algebraic expression, in terms of a, b, and c, to represent the mean of the new set of numbers obtained by
a) adding 5 to every number in the set.
Answer:
\(\frac{a + b + c}{3}\) + 5

Explanation:
It is given that a data set consists of three numbers, a, b, and c
We know that,
Mean = \(\frac{\text {The sum of the numbers in the data set}}{\text {The number of values present in the data set}}\)
According to the given condition,
We have to add 5 to each value
So, The sum of the numbers = (a + 5) + (b + 5) + (c + 5)
= (a + b + c) + 15
So, The mean of the new set of numbers = \(\frac{(a + b + c) + 15}{3}\)
= \(\frac{a + b + c}{3}\) + 5
Hence, the mean of the new set of numbers is \(\frac{a + b + c}{3}\) + 5

b) doubling every number in the set.
Answer:
\(\frac{2}{3}\) (a + b + c)

Explanation:
Given that a data set consists of three numbers, a, b, and c.
We know that,
Mean = \(\frac{\text {The sum of the numbers in the data set}}{\text {The number of values present in the data set}}\)
According to the given condition,
We have to double each value i.e., we have to multiply each value with 2
So, The sum of the numbers = (a + a) + (b + b) + (c + c)
= 2a + 2b + 2c
= 2(a + b + c)
So, The mean of the new set of numbers = \(\frac{2(a + b + c)}{3}\)
= \(\frac{2}{3}\) (a + b + c)
Hence, the mean of the new set of numbers is \(\frac{2}{3}\) (a + b + c)

c) halving every number in the set.
Answer:
\(\frac{1}{6}\) (a + b + c)

Explanation:
Given that, A data set consists of three numbers, a, b, and c.
We know that,
Mean = \(\frac{\text {The sum of the numbers in the data set}}{\text {The number of values present in the data set}}\)
According to the given condition,
We have to half each value i.e., we have to multiply each value with 0.5 or \(\frac{1}{2}\)
So, The sum of the numbers = (a × 0.5) + (b × 0.5) + (c × 0.5)
= 0.5a + 0.5b + 0.5c
= 0.5(a + b + c)
So, The mean of the new set of numbers = \(\frac{0.5(a + b + c)}{3}\)
= \(\frac{0.5}{3}\) (a + b + c)
= \(\frac{1}{6}\) (a + b + c)
Hence, the mean of the new set of numbers is \(\frac{1}{6}\) (a + b + c)

Question 16.
The table shows the mean scores of three classes in a history test.

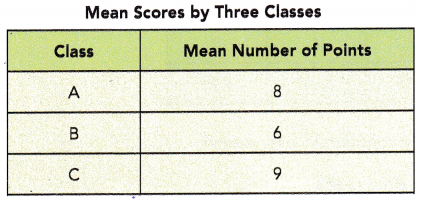
The mean score of all the students in classes A and B combined is 6.8
The mean score of all the students in classes B and C combined is 7.
If the number of students in classes A, B, and C are denoted by a, b, and c respectively, find the ratio a: b: c.

Answer:
a : b : c = 4 : 6 : 3

Explanation:
Let number of students in A = a
Let number of students in B = b
Let number of students in C = c

Total score of A ÷ a = 8
Total score of A = 8 x a = 8a

Total score of B ÷ b = 6
Total score of B = 6 x b = 6b

Total score of C ÷ c = 9
Total score of C = 9 x c = 9c

Total score of (A + B) ÷ (a + b) = 6.8
Total score of (A + B) = 6.8 x (a + b) = 6.8a + 6.8b
Total score of A + Total score of B = 6.8a + 6.8b
8a + 6b = 6.8a + 6.8b
1.2a = 0.8b
3a = 2b
a : b = 2 : 3

Total score of (B + C) ÷ (b + c) = 7
Total score of (B + C) = 7 x (b + c) = 7b + 7c
Total score of B + Total score of C = 7b + 7c
6b + 9c = 7b + 7c
b = 2c
b : c = 2 : 1

now we have
[a : b = 2 : 3] x 2
[b : c = 2 : 1] x 3

a : b = 4 : 6
b : c = 6 : 3

a : b : c = 4 : 6 : 3

Question 17.
Math Journal Find five different numbers whose mean is 12. Explain your strategy.
Answer:
Answers may vary.
The five different numbers whose mean is 12 are 10, 11, 12, 13 and14.

Explanation:
The mean is the average of the numbers.
Add up all the numbers, then divide by how many numbers there are.
10 + 11 + 12 + 13 + 14 = 65
So, divide the sum by the count or number of terms.
65 ÷ 5 = 12