Math in Focus Grade 6 Chapter 14 Lesson 14.2 Answer Key Median

This handy Math in Focus Grade 6 Workbook Answer Key Chapter 14 Lesson 14.2 Median detailed solutions for the textbook questions.

Math in Focus Grade 6 Course 1 B Chapter 14 Lesson 14.2 Answer Key Median

Math in Focus Grade 6 Chapter 14 Lesson 14.2 Guided Practice Answer Key

Find the median of each data set.

Question 1.
The data set shows the weights of a group of students.
109 lb, 86 lb, 117 lb, 97 lb, 98 lb
Ordered from least to greatest:
lb, Ib, lb, lb, lb
The median weight is ____ pounds.
Answer:
98 lb

Explanation:
It is given that the data set shows the weights of a group of students.
109 lb, 86 lb, 117 lb, 97 lb, 98 lb
Now, arrange the given weights of the group of students from the least to the greatest.
So, the order of the weights from the least to the greatest is:
86 lb, 97 lb, 98 lb, 109 lb, 117 lb
Now, from the given data set,
The number of given weights is: 5
We know that, when a data set has an odd number of values,
you can identify the middle value or median by inspection.
So, the median of the given data set is: 98 lb
Hence, the median weight is 98 lb.

Question 2.
The data set shows the volumes of water (in fluid ounces) in some containers.

The median volume of water is _____fluid ounces.
Answer:
32 fluid ounces.

Explanation:
It is given that the data set shows the volumes of water (in fluid ounces) in some containers.

Now from the above containers we can observe that,
The volumes of water in the given containers are:
16 fluid ounces, 32 fluid ounces, 56 fluid ounces, 8 fluid ounces, 64 fluid ounces.
The volumes of water in the given containers from the least to the greatest are:
8 fluid ounces, 16 fluid ounces, 32 fluid ounces, 56 fluid ounces, 64 fluid ounces.
So, the number of volumes of water in the given containers is: 5
We know that when a data set has an odd number of values,
you can identify the middle value or median by inspection
So, the median volume of water is: 32 fluid ounces.

Question 3.
The data set shows the ages of a group of people.
23 years, 36 years, 28 years, 43 years, 34 years, 29 years
The two middle values are ______ years and ______ years.
Mean of the two middle values =
The median age is ______ years.
Answer:
31.5 years.

Explanation:
It is given that the data set shows the ages of a group of people.
23 years, 36 years, 28 years, 43 years, 34 years, 29 years.
Now arrange the ages of a group of people from the least to the greatest are:
23 years, 28 years, 29 years, 34 years, 36 years, 43 years.
We know that when a data set has an even number of values, identify the two middle values.
The median is the mean of these two middle values.
Now, the number of values present in a data set is: 6
So, the mean of the two middle values = \(\frac{29 + 34}{2}\)
= \(\frac{63}{2}\)
= 31.5 years
Hence, the median age is 31.5 years.
Question 4.

The data set shows the lengths of the tables that one company produces.
85 cm, 92 cm, 108 cm, 210 cm, 264 cm, 200 cm, 135 cm, 78 cm
The median length is centimeters.
Answer:
121.5 years.

Explanation:
It is given that the data set shows the lengths of the tables that one company produces.
85 cm, 92 cm, 108 cm, 210 cm, 264 cm, 200 cm, 135 cm, 78 cm
Now arrange the lengths of the tables from the least to the greatest are:
78 cm, 85 cm, 92 cm, 108 cm, 135 cm, 200 cm, 210 cm, 264 cm
We know that when a data set has an even number of values, identify the two middle values.
The median is the mean of these two middle values.
So, the number of values present in a data set is: 8
The mean of the two middle values = \(\frac{108 + 135}{2}\)
= \(\frac{243}{2}\)
= 121.5 years
Hence, the median length is 121.5 years.

Question 5.
The data set shows the distances that a group of students ran during an exercise.
\(\frac{1}{2}\) mi, \(\frac{7}{8}\) mi, \(\frac{3}{4}\) mi, \(\frac{5}{8}\) mi
The median distance was ___ miles.
Answer:
\(\frac{11}{16}\) miles

Explanation:
It is given that the data set shows the distances that a group of students ran during an exercise.
\(\frac{1}{2}\) mi, \(\frac{7}{8}\) mi, \(\frac{3}{4}\) mi, \(\frac{5}{8}\) mi
Now arrange the distance that a group of students ran during an exercise from the least to the greatest is:
\(\frac{1}{2}\) mi, \(\frac{5}{8}\) mi, \(\frac{3}{4}\) mi, \(\frac{7}{8}\) mi
We know that when a data set has an even number of values, identify the two middle values.
The median is the mean of these two middle values
So, the number of values present in a data set is: 4
The mean of the two middle values = (\(\frac{5}{8}\) + \(\frac{3}{4}\)) × \(\frac{1}{2}\)
= \(\frac{11}{8}\) × \(\frac{1}{2}\)
= \(\frac{11}{16}\) mi
Hence, the median distance is \(\frac{11}{16}\) miles.

Complete. Use the data in the dot plot.

The dot plot shows the weights of a group of immature white-tailed deer fawns. Each dot represents 1 fawn.

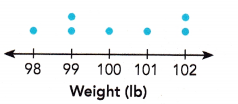
Question 6.
The median weight of the fawns is _____ pounds.
Answer:
100 pounds.

Explanation:
It is given that the dot plot shows the weights of a group of immature white-tailed deer fawns and each dot represents 1 fawn.
The given dot plot is:

We observe that, the total number of fawns is: 7
Now arrange the order of the fawns from the least to the greatest is:
1 fawn, 1 fawn, 1 fawn, 2 fawns, 2 fawns
We know that when a data set has an odd number of values,
you can identify the middle value or median by inspection.
So, the median weight of the fawns = The middle value of the weights of a group of immature white-tailed deer fawn.
= 100 × (The number of fawns corresponding to the weight of 100 lb)
= 100 × 1
= 100 lb
Hence, the median weight of the fawns is 100 pounds.

Question 7.
A new fawn joins the group. It weighs 101 pounds.
a) Add a dot to a copy of the dot plot above to show this information.
Answer:

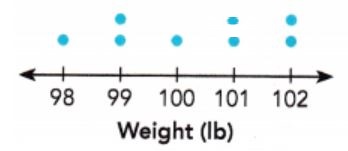
Explanation:
It is given that the dot plot shows the weights of a group of immature white-tailed deer fawns and each dot represents 1 fawn.
The given dot plot is:

A new fawn joins the group.
It weighs 101 pounds.
Hence, The dot plot that represents the given information is shown above.

b) Does this change the median of the data set? What is the median of the data set now?
Answer:
100.5 pounds.

Explanation:
From part (a), we can observe that
The new dot plot is:

Since the dots (The number of fawns) are changed, the median of the data set will also be changed.
Since the number of fawns is even, the median will be the middle value of the 4th and 5th values.
So, the median of the new data set = \(\frac{101 + 100}{2}\)
= \(\frac{201}{2}\)
= 100.5 pounds
Hence, the median of the data set now will be 100.5 pounds.

Complete. Use the data in the dot plot.

The lowest temperatures in a town are recorded over a few days. The dot plot on the right shows these temperature readings. Each dot represents 1 temperature reading.

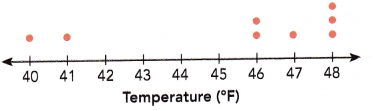
Question 8.
The mean temperature is °F.
Answer:
45.5 °F

Explanation:
It is given that the lowest temperatures in a town are recorded over a few days.
The dot plot on the right shows these temperature readings.
Each dot represents 1 temperature reading.
The given data plot is:

We know that,
Mean = \(\frac{\text {The sum of the values in a data set}}{\text {The number of values in a data set}}\)
From the given data plot we observe that,
The number of values in the given data set is: 8
So, Mean temperature = \(\frac{(40 × 1) + (41 × 1) + (46 × 2) + (47 × 1) + (48 × 3)}{8}\)
= \(\frac{40 + 41 + 92 + 47 + 144}{8}\)
= \(\frac{364}{8}\)
= 45.5°F
Hence, the mean temperature is 45.5 °F.

Question 9.
The median temperature is °F.
Answer:
44 °F

Explanation:
It is given that the lowest temperatures in a town are recorded over a few days.
The dot plot on the right shows these temperature readings.
Each dot represents 1 temperature reading.
The given data plot is:

From the above dot plot we observe that,
The total number of temperature readings is 8.
So, Median = The middle value of the temperature readings.
Hence, The median temperature is 44 °F.

Question 10.
of the temperature readings recorded are higher than the mean temperature.
Answer:
46 °F, 47 °F, and 48 °F

Explanation:
It is given that the lowest temperatures in a town are recorded over a few days.
The dot plot on the right shows these temperature readings.
Each dot represents 1 temperature reading.
The given dot plot is:

From Question 8, we observe that,
The mean temperature is 45.5 ° F.
Hence, the temperature recordings that are higher than the mean temperature are 46 °F, 47 °F, and 48 °F.

Question 11.
Which of the two measures of central tendency, the mean or the median, better describes the data set? Justify your answer.
Answer:
The median describes the given data set better.

Explanation:
From Question 8 and Question 9,
We can observe that,
The mean is 45.5 °F. However, more than 1 temperature reading is less than 45.5 °F.
So, the mean does not describe the data set well.
The median is 44 °F.
It describes the data set better because most of the data values cluster around 44 °F.
Hence, the median describes the given data set better.

Hands-On Activity

COLLECTING AND TABULATING DATA TO FIND MEDIAN

Materials

• blank table

Work in pairs.

Step 1: Refer to the first paragraph of the chapter opener. Count the number of times the letter ‘e’ appears in each line. Record your answers in a copy of the table below.

Answer:

Step 2: Find the mean and median number of times the letter ‘e’ appears in each line.
Answer:
mean =7.833
median = 8.5

Explanation:
The mean = \(\frac{Sum of a set of items}{Number of items}\)
mean = \(\frac{11 + 10 + 8 + 3 + 9 + 6}{6}\)
mean = 7.833
median : Middle value is the median of a given data set.
The given data set {3, 6, 8, 9, 10, 11} contains even number and 8 and 9 are in the middle.
the average of the 8 and 9 is the median of the given data set.
median = \(\frac{8 + 9}{2}\)
median = 8.5

Math in Focus Course 1B Practice 14.2 Answer Key

Find the median of each data set.

Question 1.
9, 8, 7, 11, 7, 16, 3
Answer:
median = 8

Explanation:
median : Middle value is the median of a given data set.
The given data set {9, 8, 7, 11, 7, 16, 3}contains odd numbers.
So, arrange them in ascending order {3, 7, 7, 8, 9, 11, 16} to find the median.
Number 8 in the middle of the order sequence is the median.

Question 2.
31, 43, 12, 25, 54, 18
Answer:
median = 18.5

Explanation:
median : Middle value is the median of a given data set.
The given data set {12, 18, 25, 31, 43, 54} contains even number and are arranged in the ascending order.
12 and 25 are in the middle.
the average of the 12 and 25 is the median of the given data set.
median = \(\frac{12 + 25}{2}\)
median = \(\frac{37}{2}\)
median = 18.5

Question 3.
3.2, 1.5, 2.6, 3.5, 6.9, 5.8, 2.4
Answer:
median = 3.2

Explanation:
median : Middle value is the median of a given data set.
The given data set {3.2, 1.5, 2.6, 3.5, 6.9, 5.8, 2.4} contains odd numbers.
Arrange them in ascending order{1.5, 2.4, 2.6, 3.2, 3.5, 5.8, 6.9} to find the median.
So, 3.2 in the middle of the order sequence is the median.

Question 4.
32.6, 72.6, 28.7, 45.4, 83.6, 69.9
Answer:
median = 57.65

Explanation:
median : Middle value is the median of a given data set.
The given data set {32.6, 72.6, 28.7, 45.4, 83.6, 69.9} contains even numbers.
Arrange the numbers in the ascending order{28.7, 32.6, 45.4, 69.9, 72.6, 83.6} to fid the median.
So, the numbers 45.4 and 69.9 are in the middle.
Take the average of the 45.4 and 69.9 is the median of the given data set.
median = \(\frac{45.4 + 69.9}{2}\)
median = \(\frac{115.3}{2}\)
median = 57.65

Solve. Show your work.

Question 5.
The number of points scored by seven students in a language test are 68, 46, 74, 58, 63, 91, and 85. Find the median score.
Answer:
median = 68

Explanation:
median : Middle value is the median of a given data set.
The given data set {68, 46, 74, 58, 63, 91, 85} contains odd numbers.
Arrange the given data in ascending order {46, 58, 63, 68, 74, 85, 91} to find the median.
So, number 68 in the middle of the order sequence is the median.

Question 6.
The data set shows the number of goals scored by a soccer team in eight matches.
0, 2, 3, 1, 4, 2, 5, 2
Find the median number of goals scored.
Answer:
median = 57.65

Explanation:
median : Middle value is the median of a given data set.
The given data set {0, 2, 3, 1, 4, 2, 5, 2} contains even numbers.
Arrange the given data in ascending order {0, 1, 2, 2, 2, 3, 5} to find the median.
So, the numbers 2 and 2 are in the middle.
Take the average of the 2 and 2 is the median of the given data set.
median = \(\frac{2 + 2}{2}\)
median = \(\frac{4}{2}\)
median = 2

Question 7.
The costs of four cell phones are $345, $400, $110, and $640. Find the median cost.
Answer:
median = 372.5

Explanation:
median : Middle value is the median of a given data set.
The given data set {$345, $400, $110, and $640} contains even numbers.
Arrange the given data set in ascending order {$110, $345, $400, $640} to find the median.
So, the numbers $345 and $400 are in the middle.
Take the average of the 345 and 400 is the median of the given data set.
median = \(\frac{345 + 400}{2}\)
median = \(\frac{745}{2}\)
median = 372.5

Question 8.
The volumes of water, in liters, in eight containers are 3.1, 2.8, 3.2, 4.2, 3.9, 5.6, 3.7, and 4.5. Find the median volume.
Answer:
median = 3.8

Explanation:
median : Middle value is the median of a given data set.
The given data set {3.1, 2.8, 3.2, 4.2, 3.9, 5.6, 3.7, 4.5} contains even numbers.
Arrange the given data set in ascending order {2.8, 3.1, 3.2, 3.7, 3.9, 4.2, 4.5, 5.6}
So, the numbers 3.7 and 3.9 are in the middle.
Take the average of the 3.7 and 3.9 is the median of the given data set.
median = \(\frac{3.7 + 3.9}{2}\)
median = \(\frac{7.6}{2}\)
median = 3.8

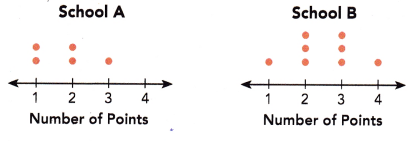
Use the data in the dot plots to answer questions 9 and 10.

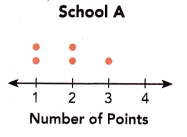
The dot plot shows the number of points scored by the members of a Quiz Bowl team in a competition between School A and School B. Each dot represents one student’s points.

Question 9.
How many team members did each school have?
Answer:
School A have 5 members.
School B have 8 members.

Explanation:
The above dot plot shows the number of points scored by the members of a Quiz Bowl team in a competition between School A and School B.
Each dot represents one student’s points.
So, count the dots on the plot of School A and School B.
School A have 5 members.
School B have 8 members.

Question 10.
What was the median number of points scored by the students from
a) School A?
Answer:
median = 2

Explanation:

median : Middle value is the median of a given data set.
The given data set {1, 1, 2, 2, 3} contains odd numbers and are arranged in the ascending order and 2 is in the middle of the order sequence.
median = 2

b) School B?
Answer:
median = 3.8

Explanation:

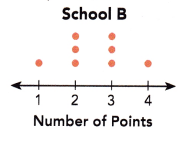
median : Middle value is the median of a given data set.
The given data set {1, 2, 2, 2, 3, 3, 3, 4} contains even number and are arranged in the ascending order.
2 and 3 are in the middle.
the average of the 2 and 3 is the median of the given data set.
median = \(\frac{2 + 3}{2}\)
median = \(\frac{5}{2}\)
median = 2.5

Use the data In the dot plot to answer questions 11 to 13.

Janice bought some dinner rolls from a bakery. The dot plot shows the prices of the dinner rolls in cents. Each dot represents 1 dinner roll.

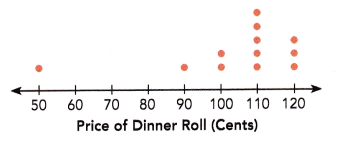
Question 11.
What is the mean price of the dinner rolls Janice bought? Round your answer to the nearest cent.
Answer:
104 cents.

Explanation:
The mean = \(\frac{Sum of a set of items}{Number of items}\)
mean = \(\frac{50 + 90 + 100 + 100 + 110 + 110 + 110 +110 + 110 + 120 + 120 + 120}{12}\)
mean = 104.2
Round the answer to the nearest cent. = 104

Question 12.
What is the median price of the dinner rolls she bought?
Answer:
$110

Explanation:
median : Middle value is the median of a given data set.
The given data set {50, 90,100, 100, 110, 110, 110, 110, 110, 120, 120, 120} contains even number and are arranged in the ascending order.
110 and 110 are in the middle.
the average of the 110 and 110 is the median of the given data set.
median = \(\frac{110 + 110}{2}\)
median = \(\frac{220}{2}\)
median = 110

Question 13.
Which of the two measures of central tendency, the mean or the median, better describes the data set? Justify your answer.
Answer:
Median

Explanation:
median : Middle value is the median of a given data set.
The given data set {50, 90,100, 100, 110, 110, 110, 110, 110, 120, 120, 120} contains even number and are arranged in the ascending order.
In this situation, we would like to have a better measure of central tendency.

Solve.

Question 14.
The median of a set of numbers is x. There are at least three numbers in the set. Write an algebraic expression, in terms of x, to represent the median of the new set of numbers obtained by

a) adding 3 to every number in the set.
Answer:
x+2, x+3, x+4

Explanation:
Given that,
The median of a set of numbers is x.
There are at least three numbers in the set.
x-1, x, x+1
x-1+3, x+3, x+1+3
x+2, x+3, x+4

b) doubling every number in the set.
Answer:
2x-2, 2x, 2x+2

Explanation:
Given that,
The median of a set of numbers is x.
There are at least three numbers in the set.
x-1, x, x+1
By doubling every number in the set we get,
2x-2, 2x, 2x+2

c) dividing every number in the set by 5 and then subtracting 2 from the resulting numbers.
Answer:
((x-1)/5) – 2, (x/5) – 2, ((x+1)/5) – 2

Explanation:
Given that,
The median of a set of numbers is x.
There are at least three numbers in the set.
x-1, x, x+1
By dividing every number in the set by 5 and then subtracting 2 from the resulting numbers.
((x-1)/5) – 2, (x/5) – 2, ((x+1)/5) – 2

d) adding 2 to the greatest number in the set.
Answer:
x-1, x, x+3

Explanation:
Given that,
The median of a set of numbers is x.
There are at least three numbers in the set.
x-1, x, x+1
By adding 2 to the greatest number in the set.
x-1, x, x+1+2
So, x-1, x, x+3

e) subtracting 3 from the least number in the set.
Answer:
x-4, x, x+1

Explanation:
Given that,
The median of a set of numbers is x.
There are at least three numbers in the set.
x-1, x, x+1
subtracting 3 from the least number in the set.
x-1, x, x+1
x-1-3, x, x+1
x-4, x, x+1

Question 15.
The median of a set of three unknown numbers is 5. If the number 3 is added to the least number in the set, give an example of the original set in which
a) the median of the new set of numbers will not be equal to 5.
Answer:
Answer vary.
4, 5, 6 is the sample.

Explanation:
x-1, x, x+1
The median of a set of three unknown numbers is 5.
If the number 3 is added to the least number in the set.
x = 5
x-1, x, x+1
4, 5 , 6
If the number 3 is added to the least number in the set.
Give an example of the original set in which,
4+3, 5 , 6
5, 6 , 7

b) the median of the new set of numbers will still be equal to 5.
Answer:
No

Explanation:
We know that the median is the middle point in a dataset.
To find the median: Arrange the data points from smallest to largest.
If the number of data points is odd, the median is the middle data point in the list.
So, the median of the above set is {5, 6 , 7} is 6.

Question 16.
The median of a set of three unknown numbers is 5. If the number 2 is subtracted from the greatest number in the set, give an example of the original set in which
a) the median of the new set of numbers will not be equal to 5.
Answer:
No

Explanation:
a) the median of the new set of numbers will not be equal to 5.
x-1, x, x+1
The median of a set of three unknown numbers is 5
4, 5, 6
If the number 2 is subtracted from the greatest number in the set,
So, the greatest number is 6.
4, 5, 6-2
4, 4, 5
We know that the median is the middle point in a dataset.
To find the median: Arrange the data points from smallest to largest.
If the number of data points is odd, the median is the middle data point in the list.
Hence, median is 4.

b) the median of the new set of numbers will still be equal to 5.
Answer:
No

Explanation:
After rearranging the numbers in ascending order,
median is 4 as shown above.