This handy Math in Focus Grade 5 Workbook Answer Key Chapter 12 Practice 1 Angles on a Line provides detailed solutions for the textbook questions.
Math in Focus Grade 5 Chapter 12 Practice 1 Answer Key Angles on a Line
In each figure, \(\overleftrightarrow{A C}\) is a line. Use a protractor to find the unknown angle measures.
Question 1.
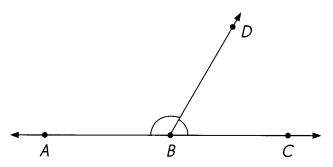
m∠DBC = ____
m∠DBA = ____
m∠DBC + m∠DBA = ___ + _____
= _____
Answer:
m∠DBC = 60°
m∠DBA = 120°
m∠DBC + m∠DBA = 60° + 120°= 180°
Explanation:
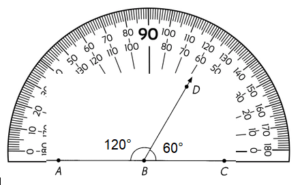
To determine to measure of the unknown angle, be sure to use the total sum of 180°.
Then take a protractor and measure m∠DBC = 60°
Then subtract m∠DBC = 60° from 180°,
We get m∠DBA = 120°
Question 2.
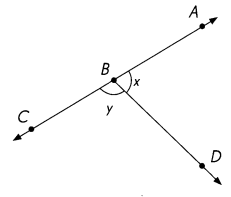
m∠x = ____
m∠y = ____
m∠x + m∠y = ___ + ___
= _____
Answer:
m∠x = 70°
m∠y = 110°
m∠x + m∠y = 70° + 110° = 180°
Explanation:
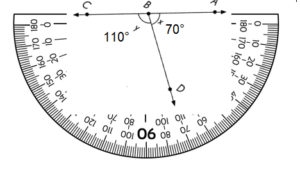
To measure the unknown angles, first take a protractor and measure m∠x = 70°
Then measure m∠y = 110°
Add both the angles m∠x + m∠y = 70° + 110° = 180°
\(\overleftrightarrow{A C}\) is a line. Use a protractor to find the unknown angle measures.
Question 3.
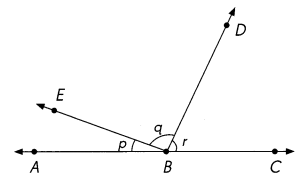
m∠p = ____
m∠q = ____
m∠r = ____
m∠p + m∠q + m∠r = ___ + ___ + ___
= ____
Answer:
m∠p = 20°
m∠q = 100°
m∠r = 60°
m∠p + m∠q + m∠r = 20° + 100° + 60°= 180°
Explanation:
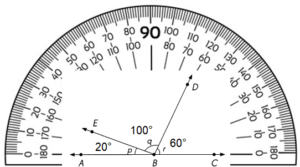
To measure the unknown angles, first take a protractor and measure m∠p = 20°
Then measure m∠q = 100°
Then measure m∠r = 60°
Add all the angles m∠p + m∠q + m∠r = 20° + 100° + 60° = 180°
Name the angles on each line.
Question 4.
\(\overleftrightarrow{X Z}\) is a line.
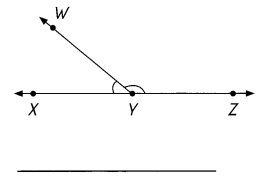
Answer:
m∠XYW = 40°
m∠WYZ = 140°
m∠XYW + m∠WYZ = 40°+ 140° = 180°
Explanation:
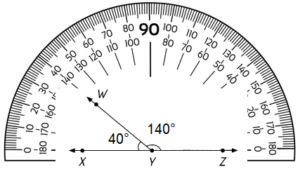
To determine to measure of the unknown angle, be sure to use the total sum of 180°.
Then take a protractor and measure m∠XYW = 40°, an angle less than 90° is acute angle.
Then take a protractor and measure m∠WYZ = 140°, an angle more than 90° is obtuse angle.
Add both the angles m∠XYW + m∠WYZ = 40°+ 140° = 180°
Question 5.
\(\overleftrightarrow{P R}\) is a line.
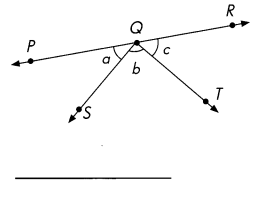
Answer:
m∠PQS = m∠a = 40° Acute Angle
m∠TQS = m∠b = 90° Right Angle
m∠TQR = m∠c = 50° Acute Angle
m∠PQS + m∠TQS + m∠TQR = 40°+ 90° + 50° = 180° Straight Angle
Explanation:
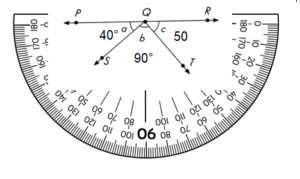
To determine to measure of the unknown angle, be sure to use the total sum of 180°.
Then take a protractor and measure m∠PQS = m∠a = 40° Acute Angle, an angle less than 90° is acute angle.
Then take a protractor and measure m∠TQS = m∠b = 90° Right Angle.
Then take a protractor and measure m∠TQR = m∠c = 50° Acute Angle
Add all the angles m∠PQS + m∠TQS + m∠TQR = 40°+ 90° + 50° = 180° Straight Angle.
Name each set of angles on a line.
Question 6.
\(\overleftrightarrow{A C}\) is a line.
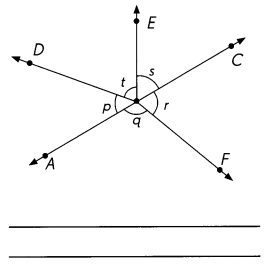
Answer:
m∠p = 50°
m∠q = 120°
m∠r = 60°
m∠s = 60°
m∠t = 70°
∠p + ∠q + ∠r + ∠s + ∠t = 50° + 120° + 60°+ 60°+ 70° = 360°
Explanation:
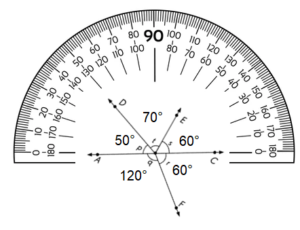
m∠p and m∠q are Vertical angles where the two angles cross each other.
m∠r , m∠t and m∠s are acute angle, where the angle is less than 90°
Question 7.
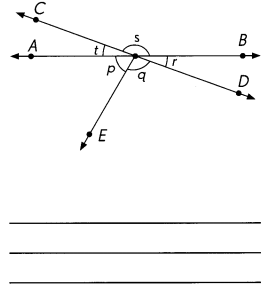
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are line.
Answer:
∠p = 60°
∠q = 100°
∠r = 20°
∠s = 160°
∠t = 20°
∠p + ∠q + ∠r + ∠s + ∠t = 60° + 100° + 20°+ 160°+ 20° = 360°
Explanation:
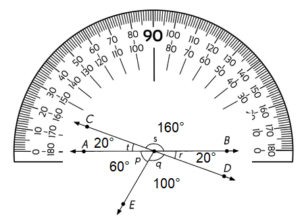
∠p, ∠r and ∠t are acute angles, where the angle is less than 90°
∠q and ∠s are obtuse angles, where the angles is more than 90°
Find the unknown angle measures.
Question 8.
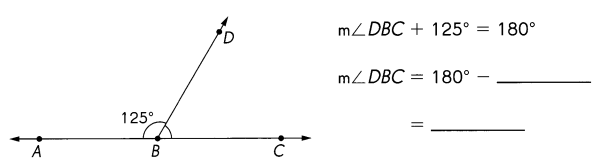
\(\overleftrightarrow{A C}\) is a line. Find the measure of ∠DBC.
Answer:
Explanation:
To determine to measure of the unknown angle, be sure to use the total sum of 180°.
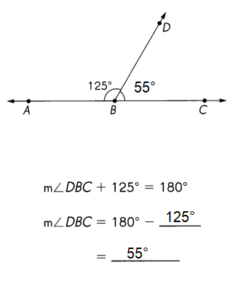
Given m∠DBC + 125° = 180°
m∠DBC – 180° = 125° = 55°
Question 9.
\(\overleftrightarrow{E G}\) is a line. Find the measure of ∠HFE.
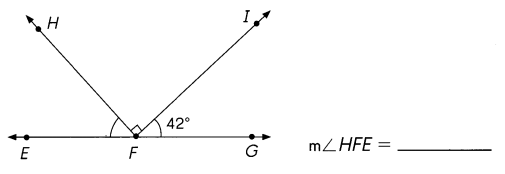
Answer:
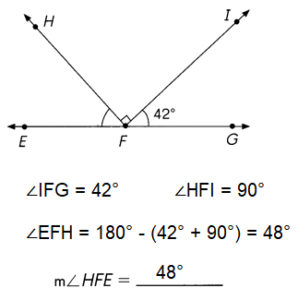
Explanation:
To determine to measure of the unknown angle, be sure to use the total sum of 180°.
Given ∠FIG = 42° = 180°
∠HFI = 90°
∠EFH = 180° – (42° + 90°)
= 180° – 132° = 48°
Find the unknown angle measures.
Question 10.
\(\overleftrightarrow{O Q}\) is a line. Find the measure of ∠SPT.
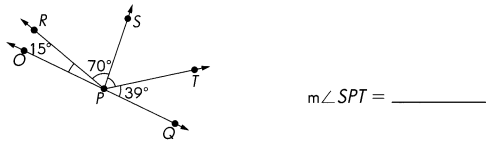
Answer:
m∠SPT =180° – (15°+70°+39°) = 56°
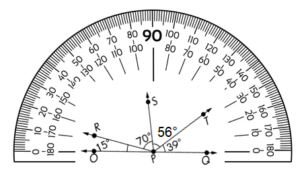
Explanation:
To determine to measure of the unknown angle, be sure to use the total sum of 180°.
Given ∠POR = 15°
∠RPS = 70°
∠TPQ = 39°
m∠SPT = 180° – (∠POR +∠RPS +∠TPQ )
m∠SPT =180°- (15°+70°+39°) = 56°
Question 11.
\(\overleftrightarrow{A C}\) is a line. Find the measure of ∠EBF.
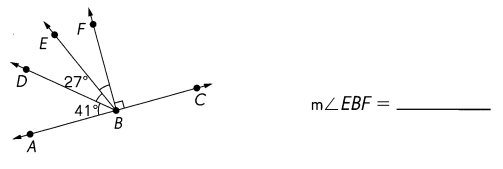
Answer:
m∠EBF =180° – (41° + 27° + 90°) = 180° – 158° = 22°
Explanation:
To determine to measure of the unknown angle, be sure to use the total sum of 180°.
Given ∠DBA = 41°
∠DBE = 27°
∠FBC = 90°
m∠EBF = 180° – (∠DBA +∠DBE +∠FBC )
m∠EBF =180°- (41°+27°+90°) = 22°
Question 12.
\(\overleftrightarrow{J K}\) is a line. Find the measure of ∠y and ∠z.
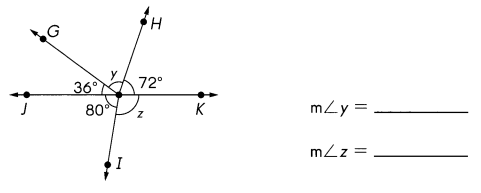
Answer:
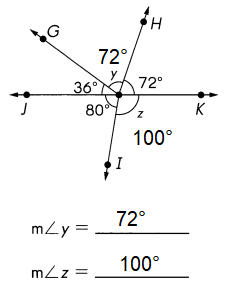
Explanation:
Angles formed by two rays lie in the plane that contains the rays.
Angles are also formed by the intersection of two planes.
Given:
∠JOI = 80°
∠JOG = 36°
∠GOH= 72°
m∠y = 180° – (∠JOG+∠GOH)
m∠y =180°- (36°+72°)
=180°- 108°
= 72°
m∠z =180°- ∠JOI
= 180° – 80°
= 100°
Question 13.
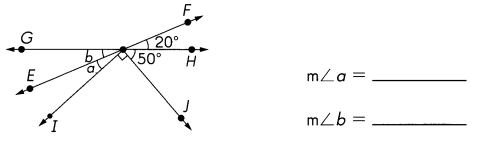
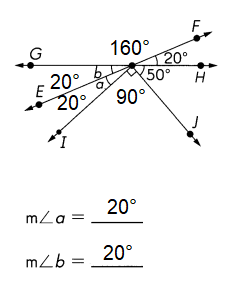
\(\overleftrightarrow{E F}\) and \(\overleftrightarrow{G H}\) are line. Find the measure of ∠a and ∠b.
Answer:
Explanation:
Angles formed by two rays lie in the plane that contains the rays are called vertex of the angle.
Angles are also formed by the intersection of two planes.
Given:
∠GOF = 160°
∠FOH = 20°
∠HOJ= 50°
∠JOI = 90°
m∠a =180°- ∠GOF
= 180° – 160°
= 20°
m∠b= 180° – (∠HOJ+∠FOH+∠JOI )
=180°- (50°+20°+90°)
=180°- 160°
= 20°