This handy Math in Focus Grade 5 Workbook Answer Key Chapter 12 Angles provides detailed solutions for the textbook questions.
Math in Focus Grade 5 Chapter 12 Answer Key Angles
Math Journal
Check the box for each correct statement. Then explain your answer.
Question 1.
\(\overleftrightarrow{X Y}\) is a line.
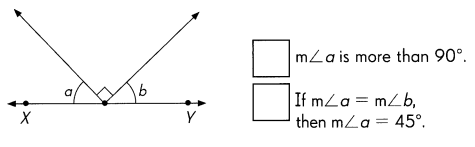
Answer:

Explanation:
The XY is a line and the angle on a straight line is 180°, known as straight angle.
Angle POQ is 90° as per the given information in the diagram.
180° – 90° = 90°
Angle ∠XOP and ∠YOQ are equal angle = 45°
Question 2.
\(\over left right arrow{A B}\) and \(\over left right arrow{C D}\) meet at O.
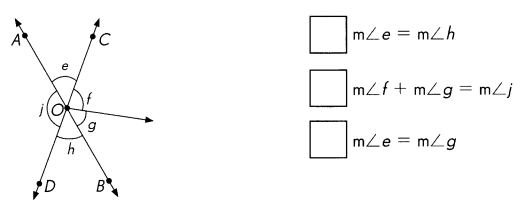
Answer:
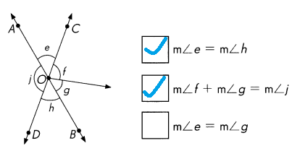
Explanation:
\(\over left right arrow{A B}\) is a line and \(\over left right arrow{C D}\) is a line are crossed at O, the opposite angles are same.
So, m∠e = m∠h and
m∠f + m∠g = m∠j are true statements.
Put On Your Thinking Cap!
Challenging Practice
Find the unknown angle measures. Explain.
Question 1.
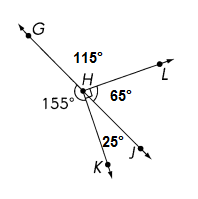
\(\over left right arrow{G J}\) is a line. ∠LHK is a right angle. Find the measure of ∠LHJ.
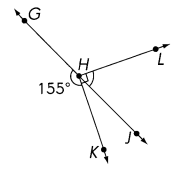
Answer: 65°
Explanation:
Given information
GJ is a straight line, ∠LHK = 90°
∠JHK = 180° – ∠JHK
= 180° – 155° = 25°
∠JHK = ∠LHK – ∠JHK
= 90° – 25° = 65°
Question 2.
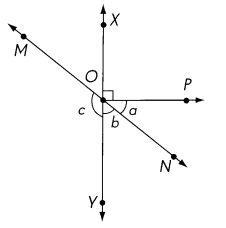
\(\over left right arrow{M N}\) and \(\over left right arrow{X Y}\) meet at O and m ∠a = m ∠b. Find the measure of ∠c.
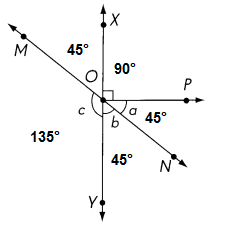
Answer: 135°
Explanation:
\(\over left right arrow{X Y}\) is a line and \(\over left right arrow{M N}\) is a line are crossed at O, the opposite angles are same.
given information m∠a = m∠b and ∠XOP = 90
as XOY is a straight line, the angle is 180°
90° + m∠a + m∠b = 180°
∠c = 180° -∠XOM= 180 – 45° = 135°
Question 3.
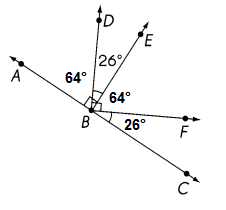
\(\over left right arrow{A C}\) is a line. ∠ABE and ∠DBF are right angles. Find the measure of ∠FBC.
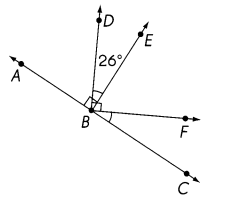
Answer: 26°
Explanation:
∠ABE and ∠DBF = 90°
∠EBF = ∠DBF – ∠DBE
= 90° – 26° = 64°
∠ABD = ∠ABE – ∠DBE
= 90° – 26° = 64°
∠FBC = 180 – (∠ABE + ∠EBF)
= 180° – (90° + 64°)
=180° – 154° = 26°
Question 4.
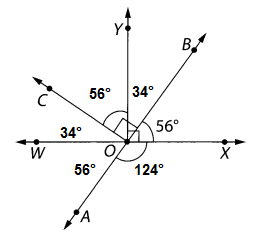
\(\over left right arrow{A B}\) and \(\over left right arrow{W X}\) meet at O. ∠YOX are right angles. Find the measures of ∠AOX and ∠COY.
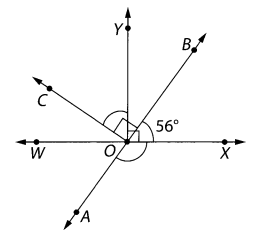
Answer:
∠AOX = 124°
∠COY = 56°
Explanation:
90° – 56° = 34°
90° – 34° = 56°
∠COY = ∠COB – ∠BOY
= 90° – 34° = 56°
∠AOX = ∠WOX – ∠AOW
=180°- 56° = 124°
Put on Your Thinking cap!
Problem Solving
Solve.
Question 1.
\(\over left right arrow{J K}\) and \(\over left right arrow{L M}\) are lines.
Check the box for each correct statement.
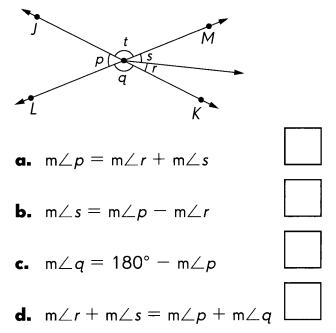
Answer:
\(\over left right arrow{J K}\) and \(\over left right arrow{L M}\) are lines.
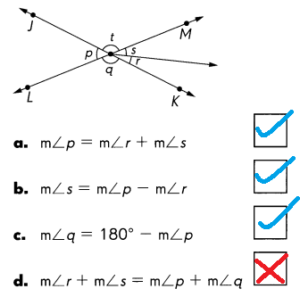
Explanation:
\(\over left right arrow{J K}\) is a line and \(\over left right arrow{L M}\) is a line are crossed at O, the opposite angles are same.
so, m∠r + m∠s = m∠p + m∠q is the wrong statement.
Question 2.
\(\over left right arrow{A B}\), \(\over left right arrow{C D}\), and \(\over left right arrow{E F}\) meet at O. Find the sum of the measures of ∠AOC, ∠FOD, and ∠BOE.
m∠AOC + m∠FOD + m∠BOE = _____
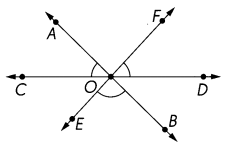
Answer: 180°
Explanation:
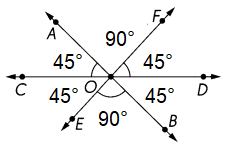
m∠AOC = 45°
m∠FOD = 45°
m∠BOE = 90°
m∠AOC + m∠FOD + m∠BOE = 180°
Question 3.
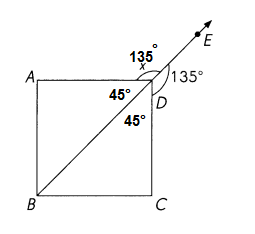
ABCD is a square. \(\over right arrow{B E}\) is a ray. Find the measure of ∠x.
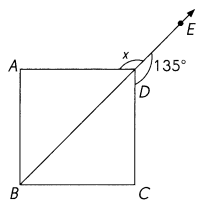
Answer: 135°
Explanation:
As BE is a straight line and the angle is 180° at point D
and a square is ABCD is with 90° angle formed at point D
the ange ∠EDC is 135° angle ∠CDB is 45° and ∠ADB is also 45°
now the
∠x = ∠EDB – ∠ADB
= 180° – 45° = 135°
Question 4.
How many degrees does the hour hand of a clock turn between 3 P.M. and 7:30 P.M.?
Answer: 135°
Explanation:
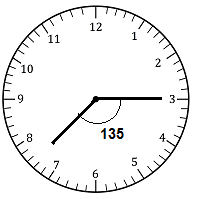
Hour hand at 3PM is at 3 and 7:30 as shown in the clock diagram
Total angle is 360°, keep it in mind
and 360° divide in 12 parts
each part is of 30°
from hours hand 3 to 7 :30 its 135°
Question 5.
\(\over left right arrow{A B}\) is a line. The measures of ∠a and ∠b are whole numbers.
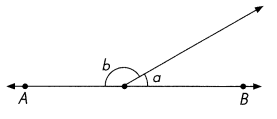
If the measure of ∠b is twice that of ∠a, find the measures of ∠a and ∠b.
Answer:
∠a = 60°
∠b = 120°
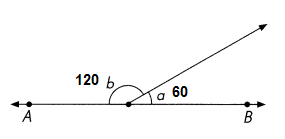
Explanation:
Here the hint is angle ∠b is twice that of ∠a, and The AB is a line and the angle on a straight line is 180, known as straight angle
∠b + ∠a = 180°
2∠a + ∠a = 180°
3∠a = 180°
∠a = 180°/3 = 60°
∠a = 60°
∠a = 60°
∠b = 2x∠a = 120°