Math in Focus Grade 8 Chapter 2 Lesson 2.3 Answer Key Multiplying and Dividing in Scientific Notation

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 2 Lesson 2.3 Multiplying and Dividing in Scientific Notation to finish your assignments.

Math in Focus Grade 8 Course 3 A Chapter 2 Lesson 2.3 Answer Key Multiplying and Dividing in Scientific Notation

Math in Focus Grade 8 Chapter 2 Lesson 2.3 Guided Practice Answer Key

Complete.

Question 1.
In the 19th century, the Law Courts of Brussels was the largest building ever built. Its base area measures about 1.6 • 10² meters by 1.5 • 10² meters. Find the approximate base area of the building.
Approximate base area =
Length • Width

The area enclosed by the outer wall is approximately square meters.
Answer:
Given that Brussels was the largest building ever built.
Its base area measures about 1.6 × 102 meters by 1.5 × 102 meters it means
Length = 1.6 × 10²
Width = 1.5 × 10²
We know that
Base area = length × width
Base area = 1.6 × 1 0² × 1.5 × 10²
= 1.6 × 1.5 × 10⁴
= 2.4 × 10⁴ m²
The area enclosed by the outer Wall is approximately 2.4 × 10⁴ square meters.

Question 2.
The outer wall of Angkor Wat, a World Heritage site in Cambodia, encloses an area of about 1.02 • 10³ meters by 8.02 • 10² meters. Find the approximate area enclosed by the outer wall.
Approximate area enclosed by outer wall
= Length • Width

The area enclosed by the outer wall ¡s approximately square meters.
Answer:
Given that the length of a world Heritage site in Cambodia is 1.02 × 10³
The width of a world Heritage site in Cambodia is 8.02 × 10²
Area enclosed by the outer Wall = length × width
= 1.02 × 10³ × 8.02 × 10²
= 1.02 × 8.02 × 10⁵
= 8.1804 × 10⁵
The area enclosed by the outer Wall is approximately 8.1804 × 10⁵

Complete. Round each coefficient answer to the nearest tenth.

Question 3.
The Jean-Luc Lagardere plant in France is the second largest building in the world. It has an approximate volume of 5.6 • 10⁶ cubic meters. The NASA vehicle assembly building in Florida has a volume of about 3.7 • 10⁶ cubic meters. How many times as great as the volume of the NASA vehicle assembly building is the volume of the Jean-Luc Lagardere plant?

The volume of the Jean-Luc Lagardere plant is about times as great as the volume of the NASA vehicle assembly building.
Answer:
Given that the volume of Jean-Luc Lagardere plant in France is 5.6 × 10⁶ cubic meters
And the volume of the NASA vehicle assembly building is 3.7 × 10⁶ cubic meters
Now the volume of Jean-Luc Lagardere plant /volume of NASA vehicles assembly building is 5.6 × 10⁶/3.7 × 10⁶
= 5.6/3.7 × 10⁶/10⁶
= 20.72 cubic meters
The volume of the Jean-Luc Lagardere plant is 20.72 cubic meters great as the volume of the NASA vehicle assembly building.

Question 4.
The Abraj Al-Bait towers in Saudi Arabia has a floor area of about 1.5 • 10⁶ square meters. The Palazzo in Las Vegas has an approximate floor area of 6.5 • 10⁵ square meters. How many times as great as the floor area of the Palazzo is the floor area of the Abraj Al-Bait towers?

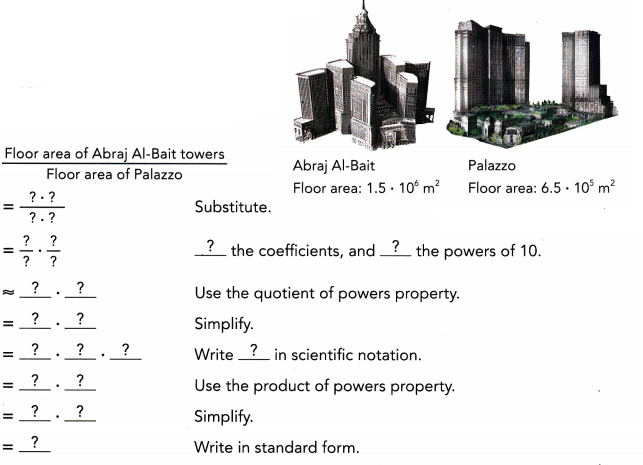
The floor area of the Abraj Al-Bait towers is approximately times greater than the floor area of the Palazzo.
Answer:
The floor area of Abraj Al-Bait towers in saudi Arabia is 1.5 × 10⁶ m²
The floor area of Palazzo in Las Vegas is 6.5 × 10⁵ m²
Therefore the floor area of Abraj AL-Bait towers/floor area of Palazzo
= 1.5 × 10⁶/6.5 × 10⁵
= 1.5/ 6.5 × 10⁶/10⁵
= 0.23 × 10¹
= 2.3 m²
The floor area of the Abraj Al-Bait Towers is approximately 2.3 m² times greater than the floor area of the Palazzo.

Math in Focus Course 3A Practice 2.3 Answer Key

Evaluate each expression in scientific notation, and round the coefficient to the nearest tenth.

Question 1.
7.45 • 10⁶ • 5.4 • 10^-6
Answer:
7.45 • 10⁶ • 5.4 • 10-6
Bases are equal powers should be added
= 7.45 • 5.4
= 40.23
40.23 rounded to the nearest tenth is 40

Question 2.
6.84 • 10^-5 • 4.7 • 10¹⁰
Answer:
6.84 • 10-5 • 4.7 • 1010
Bases are equal powers should be added.
6.84 • 4.7 • 10⁵
32.148 • 10⁵
32.148
32.148 rounded to the nearest tenth is 32.1

Question 3.
5.75 • 10^-5 ÷ (7.15 • 10⁷)
Answer:
Given that
5.75 • 10-5 ÷ (7.15 • 107)
Here 10-5 /107 = 1/10²
So, 5.75 ÷ 7.15 × 10-2
0.804 × 10-2
0.804 × 10-2 is rounded to the nearest tenth is 0.8 × 10-2

Question 4.
8.45 • 10¹¹ ÷ (1.69 • 10^-8)
Answer:
Given that
8.45 • 1011 ÷ (1.69 • 10-8)
Here 1011 /10-8 = 10³
So, 8.45 × 10³ ÷ 1.69
5 × 10³
5 × 10³ rounded to the nearest is 5 × 10³

The table shows the approximate volumes of some planets. Use the information to answer questions 5 to 7. Round your answers to the nearest tenth.

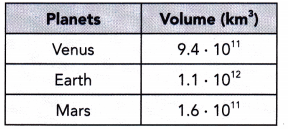
Question 5.
About how many times as great as the volume of Mars is the volume of Venus?
Answer:
Given that the volume of Mars is 1.6 × 10¹¹.
And the volume of Venus is 9.4 × 10¹¹
To find which one is great for that subtract the volume of Mars from the volume of Venus
That is 9.4 × 10¹¹/1.6 × 10¹¹
= 9.4/1.6 × 10¹¹/10¹¹
= 5.875
Therefore the volume of Venus is 5.875 times as great as Mars.
5.875 rounded to the nearest tenth of 6

Question 6.
About how many times as great as the volume of Mars is the volume of Earth?
Answer:
Given that the volume of Mars is 1.6 × 10¹¹.
And the volume of earth is 1.1 × 10¹²
To find which one is great for that we subtract the volume of earth from the volume of Mars.
That is 1.6 × 10¹¹ / 1.1 × 10¹²
= 1.6/1.1 × 10¹¹/10¹²
= 1.45 × 1/10¹
= 1.45 × 0.1
= 0.145
Therefore the volume of Mars is 0.145 as great as the Earth.
0.145 rounded to the nearest tenth is 0.1

Question 7.
About how many times as great as the volume of Venus is the volume of Earth?
Answer:
Given that the volume of Venus is 9.4 × 10¹¹
And the volume of earth is 1.1 × 10¹²
To find which one is great for that we subtract the volume of earth from the volume of Mars
That is 9.4 × 10¹¹ / 1.1 × 10¹²
= 9.4/1.1 × 10¹¹/10¹²
= 8.54 × 1/10¹
= 8.54 × 0.1
= 0.854
Therefore the volume of earth is 0.854 as great as Venus.
0.854 rounded to the nearest tenth is 0.9

Solve. Show your work.

Question 8.
Suzanne’s digital camera has a resolution of 2560 • 1920 pixels. Douglas’ digital camera has a resolution of 3264 • 2448 pixels.
a) Express the resolution of the digital cameras in prefix form to the nearest whole unit. Use the most appropriate unit.
Answer:
Suzanne: 2560 ∙ 1920 We are given the resolutions:
Douglas: 3264 ∙ 2448
2560 ∙ 1920 = 4,915, 200 ≈ 4.92 ∙ 10⁶ pixeli a) We express the resolution of Suzannes camera in prefix form:
= 4.92 megapixeli
3264 ∙ 2448 = 7, 990, 272 ≈ 7.99 ∙ 10⁶ pixeli We express the resolution of Douglas camera in prefix form:
= 7.99 megapixeli
4.99 < 7.99 b) the two numbers have the same exponent We compare the coefficients:
4.99. 10⁶ < 7.99. 10⁶

b) Whose camera has a higher resolution?
Answer:
Given that Suzanne’s digital camera has a resolution of 2560 × 1920 pixels.
= 49,15,200
And the Douglas digital camera has a resolution of 3264 × 2448 pixels.
= 79,90,272
Therefore Douglas digital camera has a higher resolution

Question 9.
Bobby downloaded pictures of a cruise ship and a ski run from the internet. The file size of the cruise ship is about 794 kilobytes while the file size of the ski run is about 2.6 megabytes.
a) What is the total file size, in megabytes and in kilobytes, of a file containing the two pictures?
Answer:
Given that the file size of the cruise ship is 794 kilobytes.
And the file size of the ski run is 2.6 megabytes.
The total file size of two pictures is 794 kilobytes + 2.6 megabytes
1 kilobyte = 0.001 megabyte
794 kilobytes = 0.794 megabytes
Therefore 0.794 + 2.6 = 3.394 megabytes.
The total file size of two pictures in megabytes is 3.394 megabytes.
1 megabyte = 1000 kilobytes
2.6 kilobytes = 2.6 × 1000 = 2600 kilobytes
Therefore the total file size of two pictures in kilobytes is 2600 kilobytes.

b) Calculate the difference in file size, in megabytes and in kilobytes, between the two pictures.
Answer:
Given that the file size of the cruise ship is 794 kilobytes.
1 kilobyte = 0.001 megabyte
794 kilobytes = 0.794 megabytes
And the file size of the ski run is 2.6 megabytes.
1 megabyte = 1000 kilobytes
2.6 megabytes = 2.6 × 1000 = 2600 kilobytes
Therefore the file size of the cruise ship is 794 kilobytes.
And the file size of the ski run is 2600 kilobytes.
The difference between the two pictures in kilobytes is 2600 – 794 = 1806
The file size of the cruise ship is 0.794 megabytes
And the file size of the ski run is 2.6 megabytes.
The difference between the two pictures in megabytes is 2.6 – 0.794 = 1.806

c) To the nearest tenth, about how many times as great as the file size of the ski run picture is the file size of the ship picture?
Answer:
Given that the file size of the cruise ship is 794 kilobytes.
Here 794 nearest to the tenth place is 790 kilobytes
1 kilobyte = 0.001 megabyte
790 kilobytes = 0.001 × 790 = 0.79 megabytes
And the file size of the ski run is 2.6 megabytes
2.6 nearest to the tenth is 3 megabytes
Therefore 3 megabytes – 0.79 megabytes
= 2.21 megabytes
The file size of the ski run picture is 2.21 megabytes great as the file size of the cruise ship.

d) Bobby saved the two pictures on a thumb drive with a capacity of 256 megabytes. Find the remaining free capacity of the thumb drive to the nearest tenth megabyte after Bobby saved the two pictures in it.
Answer:
Given that, Bobby saved two pictures on the thumb drive with a capacity of 256 megabytes.
256 nearest to the tenth is
First look at the tens place it is 5 and the digit to the right is 6.
Here the digit 6 is above 5. So, we add 1 to the tens place and place 0 on the ones place.
Therefore 256 nearest to the tenth place is 260

Question 10.
The Georgia Aquarium in Atlanta is about 2.63 • 10³ inches long, 1.26 • 10² inches wide, and 3 • 10¹ inches deep at its largest point. Find its approximate volume.
Answer:
Given that the length of a Georgia Aquarium in Atlanta is 2.63 × 10³.
The width of a Georgia Aquarium in Atlanta is 1.26 × 10².
The depth of the Georgia Aquarium in Atlanta is 3 × 10¹.
We know that the volume formula for a rectangle is length × width × height.
Georgia Aquarium is in the shape of a rectangle
Volume = 2.63 × 10³ × 1.26 × 10² × 3 × 10¹
Bases are equal powers should be added
= 2.63 × 1.26 × 3 × 10⁶
= 9.9414 × 10⁶.

Question 11.
The square base of the Great Pyramid of Khufu has a length of approximately 1.476 • 10³ feet. Its height is about 2.17 • 10² feet. Find the approximate volume of the pyramid. Write your answer in scientific notation. Round the coefficient to the nearest tenth.

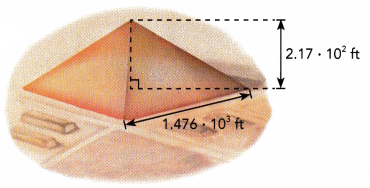
Answer:
Given that the length of a Great Pyramid of Khufu is 1.476 × 10³ feet.
And the height of the great Pyramid of Khufu is 2.17 × 10² feet.
Volume of a pyramid = ⅓ × bh
b = 1.476 × 10³
h = 2.17 × 10²
= ⅓ × 1.476 × 10³ × 2.17 × 10²
⅓ × 1.476 × 2.17 × 10⁵
1.067 × 10⁵
= 1,06,700
1,06,700 nearest to the tenth is 106700.

Question 12.
The Tropical Islands Resort is housed inside a former airplane hangar approximately 1.18 • 10³ feet long, 6.89 • 10² feet wide, and 3.51 • 10² feet high. Use the formula for the volume of a rectangular prism to approximate the volume enclosed by the resort. Round the coefficient to the nearest tenth.
Answer:
Given that the length of a tropical island resort is housed inside a former airplane hangar is 1.18 × 10³.
The wide of a tropical island resort housed inside a former airplane hangar is 6.89 × 10².
The height of a tropical island resort housed inside a former airplane hangar is 3.51 × 10².
We know that the volume of the rectangular prism is width × height × length.
Volume of the rectangular prism = 1.18 × 10³ × 6.89 × 10² × 3.51 × 10²
Bases are same powers should be added
1.18 × 6.89 × 3.51 × 10⁷
= 28.537 × 10⁷
= 28.537 × 10⁷ nearest to the tenth is 30 × 10⁷

Question 13.
The time light takes to. travel one meter in a vacuum is about 3.3 nanoseconds. To travel one mile it takes about 5.4 microseconds.
a) Find the difference, in microseconds, between the times taken by light to travel one meter and one mile in a vacuum.
Answer:
Given that, the time light takes to travel one meter in a vacuum is 3.3 nanoseconds.
The time light takes to travel one mile in a vacuum is 5.4 microseconds.
1 microsecond = 1000 nanoseconds
5.4 microseconds = 5.4 × 1000 = 5400
Difference in microseconds is 5400 – 3.3 = 5396.7

b) How many times longer, to the nearest tenth, does it take light to travel one mile than one meter?
Answer:

Question 14.
A spherical particle was found to have a radius of 3.5 • 10^-10 meter.
a) Express the diameter in the prefix form using picometers.
Answer:
Diameter of a spherical D = 2r
D = 2 × 3.5 × 10-10
= 7 × 10-8 × 10-2 meters
0.00000007 millimeters.

b) Use your answer in a), express the circumference in the prefix form using nanometers. Use 3.14 as an approximation for π.
Answer:
We know that the circumference of a spherical is C = 2πr
C = 2 × 3.14 × 3.5 × 10-10
C = 21.98 × 10-1 × 10-9
C = 21.98 × 10-1 nanometers.

Brain @ Work

Question 1.
Find the cube root of 2.7 • 10¹⁰.
Answer:
Given that 2.7 • 1010
The cube root is (2.7 • 10¹⁰) is
= (2.7 • 10,00,00,00,000)
= (27000000000)
= 3000
Therefore the cube root of 2.7 • 1010 is 3000.

Question 2.
Given that a = 3 • 10³ and b = 4 • 10², find each value.
a) 2a + b
Answer:
Given equation is 2a + b
Here a = 3 • 103
b = 4 • 102
Substitute a,b in the above given equation is
2(3 • 103) + (4 • 102)
= 2(3000)+400
= 6000+400
= 6400

b) \(\frac{2a}{b}\)
Answer:
The given equation is 2ab
Here a = 3 • 103
b = 4 • 102
Substitute a,b in the above given equation is
2(3 • 103)×(4 • 102)
2(3000)×(400)
6000×400
2400000

Question 3.
Solve each of the following. Write your answer in scientific notation using the basic unit.
a) 80 micrograms + 200 nanograms
Answer:
Convert micrograms into nanograms
1 microgram equal to 1000 nanograms
So, 80 micrograms = 1000 × 80 = 80,000 nanograms
Therefore 80,000 nanograms + 200 nanograms = 80,200 nanograms

b) 3 gigabytes – 700 megabytes
Answer:
Convert gigabytes into megabytes
1 gigabyte equal to 1024 megabytes
So, 3 gigabytes equal to 3 × 1024 = 3072 megabytes
Therefore, 3072 megabytes – 700 megabytes = 2372 megabytes.